leetcode 136.只出现一次的数字 |
用位运算就可以,相当的简单。
异或:不相同异或为1,相同异或为0。
结论:相同的数字异或为0。任何数和0异或都是自己本身。
验证:

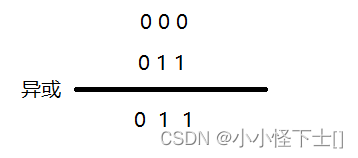
对于这道题,可以用0和数组里的每个数都异或,最终结果就只出现一次的数字。对吧?因为数组里相同的数字异或结果为0,0和只出现一次的数字异或为其本身。
题解:
class Solution {
public:
int singleNumber(vector<int>& nums)
{
int n=0;
for(int num:nums)
{
n=n^num;
}
return n;
}
};
不会用范围for的,可以走循环,自己实现,都可以。
leetcode 137. 只出现一次的数字 ||
审题:只用一个数字出现一次,其余的数字都出现三次。
举例:[2,2,2,3]
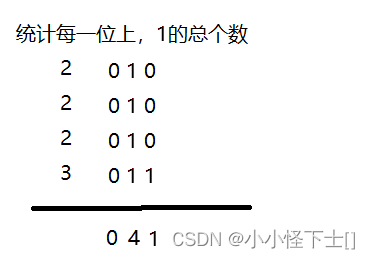
如果只有[2,2,2],那么统计结果就是0 3 0,这三个数都是可以整除3的。
因为有了[3]的加入,导致统计结果为0 4 1,可以发现第一位是可以整除3,后两位都不能整除3。那么可以得出结论:
出现一次的数 它的某个 位上是0不会影响统计结果,某个 位上是1,会影响结果(和无法整除3)。
推广:如果是:每个数都出现4次,只有一个数出现1次,和上面一样统计每个位1的总和,如果那个位上总和不能整除4,说明只出现一次的数在那个位上为1;如果依旧可以整除4,那么只出现一次的数在那个位上为0。
题解:
class Solution {
public:
int singleNumber(vector<int>& nums)
{
int n=0;
for(size_t i=0;i<32;i++)
{
int total=0;
//遍历所有nums的第i位
for(int num:nums)
{
total+=(num>>i&1);
}
//无法整除3的位,是1。
if(total%3)
{
n=n|1<<i;
}
}
return n;
}
};
代码解释:
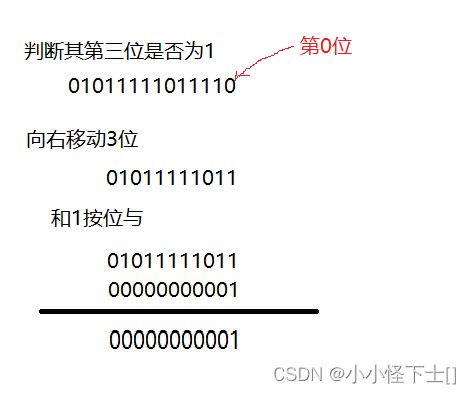
total+=(num>>i&1);
num取得是nums其中一个数,num向右移动i位,如果和1按位与结果为1,那么说明num的第i位为1。
if(total%3)
{
n=n|1<<i;
}
如果某个位1的和,无法整除3,那么那个位上是1对于只出现一次的数。
使1向左移动i位,再和n按位或,那么肯定会使n的第i位变成1。

就是这样,没毛病。
leetcode 260.只出现一次的数字 |||
审题:只有两个元素只出现一次,其余的都出现两次,要求返回一个数组,数组里有这两个元素,不在意两个元素的次序。
举例:[1,1,2,2,3,5]
用位运算可以解,这道题最简单的是用map来做,统计一下每个元素出现的次数,为1的就是我们要找到。这样做比较简单不讲,我们主要来看看用位运算如何做,也就是进阶版。

思路:
依旧先用0和数组的每个数进行异或,那么得到结果就是只出现一次的两个数的异或,这就需要我们想办法将这两个数分开。
用0去异或[1,1,2,2,3,5],得到[3,5]两数的异或结果n。
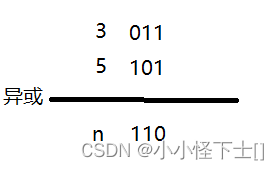
n=110,n这个数,二进制位为1的时候说明一个问题:3和5在这个位上是不同的。也就是说:我们可不可以根据这个位·为0/为1,来将数组分成两派。那么3和5必然会被分成两派。对于上面的数组可以分成[115] [223]。[115]的第一位是0,[223]的第一位是1。分成两派就好搞了。这不就是分开的第一题嘛?直接对每一派都用0去异或就可以分别得到只出现一次的数字。
我们要去找n这个数的二进制位第一次为1的位,依此来分派。
题解:
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
//得到只出现一次得两数的异或结果
int n = 0;
for (int num: nums) {
n ^= num;
}
// 防止溢出
//lsb就是n第一次位为1的位置
int lsb = (n == INT_MIN ? n : n & (-n));
int type1 = 0, type2 = 0;
for (int num: nums) {
if (num & lsb) {
type1 ^= num;
}
else {
type2 ^= num;
}
}
vector<int> arr;
arr.push_back(type1);
arr.push_back(type2);
return arr;
}
};
代码解释:
int lsb = (n == INT_MIN ? n : n & (-n));
可以用n=110来举例,n=6,-n=-6,两者按位与

可以看到n第一次位为1的位完美,展现出来了。然后可以据此分派。
if (num & lsb) {
type1 ^= num;
}
else {
type2 ^= num;
如果num&lsb==1,说明在那位上为1,如果按位与结果是0,说明那位上为0。
两派分别异或,最终得到结果。