0.前言

参考

参考: 图像分类中的基础概念+分类任务中常见损失函数介绍
参考: 损失函数（lossfunction）的全面介绍（简单易懂版）

什么是损失函数

计算真实值与预测值差距的函数。

为什么需要损失函数

算法和模型的优化目标之一是让损失函数尽可能的小，代表真实值与预测值越接近。

1.分类任务当中的损失函数

1.1.0-1损失函数

只看分类的对与错，当标签与预测类别相等时，loss为0，否则为1.
下面的公式只针对了单个样本。

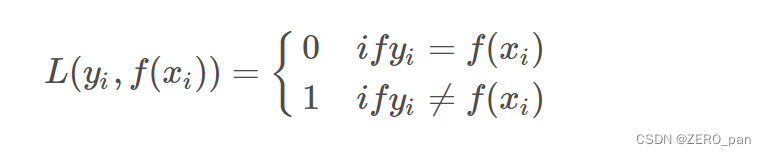
真实的优化目标，但是无法求导和优化，只有理论意义。
code:

def lossF_01(Y_true,Y_pred):
    if Y_true.shape == Y_pred.shape:
        pass
    else:
        raise ValueError('shape error')
    Y_pred = np.array(Y_pred,dtype=Y_true.dtype)
    # 以上代码是为了提高代码健壮性
    return np.sum((Y_pred!=Y_true))

1.2.L1损失函数

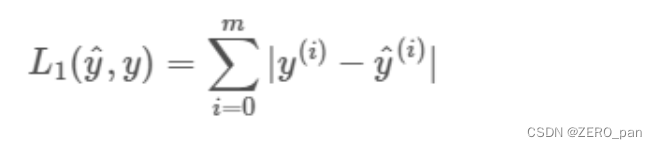
code:

def lossF_L1(Y_true,Y_pred):
    if Y_true.shape == Y_pred.shape:
        pass
    else:
        raise ValueError('shape error')
    Y_pred = np.array(Y_pred,dtype=Y_true.dtype)
    # 以上代码是为了提高代码健壮性
    return np.sum(np.absolute(Y_true-Y_pred))

1.3.交叉熵损失函数

交叉熵

熵表示热力学系统的无序程度，在信息学中用于表示信息多少，不确定性越大，概率越低，则信息越多，熵越高。

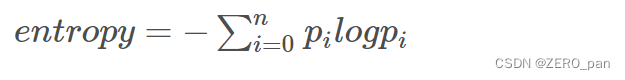
在人工智能中

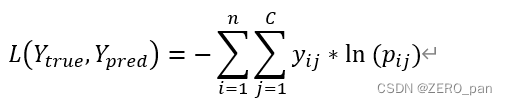
• n是样本数量
• C是类别数量
• yij表示第i个样本在第j类的真实标签
• pij表示第i个样本在第j类的预测概率

例子

二分类的例子，labe:0 or 1 。有一个样本，标签是1，onehot之后变成(0,1)

第i个样本在第1类的的真实标签是0，在第2类的真实标签是1

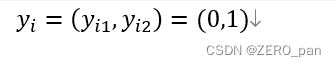
第i个样本在第1类的预测概率是0.2，在第2类的预测概率是0.8

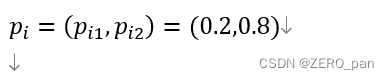
那么这个样本的交叉熵损失就是

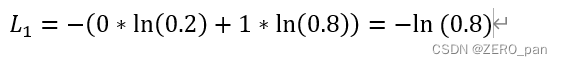
单个样本损失函数L1取值范围(0,+无穷)

多类别，我以三分类为例

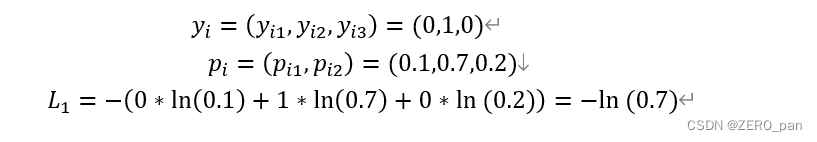
code:

def lossF_cross_entropy(Y_true,Y_pred_p):
    if Y_true.shape == Y_pred_p.shape:
        pass
    else:
        raise ValueError('shape error')

    return torch.sum(-1*torch.sum(torch.multiply(Y_true,torch.log(Y_pred_p)),dim=-1))

if __name__=='__main__':
    Y_true = np.array([0,1,0,1,0,1,1,0])
    Y_true = torch.from_numpy(Y_true).to(torch.long)
    Y_true = torch.nn.functional.one_hot(Y_true)
    '''
    tensor([
        [1, 0],
        [0, 1],
        [1, 0],
        [0, 1],
        [1, 0],
        [0, 1],
        [0, 1],
        [1, 0]])
    '''
    Y_pred_p = torch.tensor([
        [0.9,0.1],
        [0.1,0.9],
        [0.8,0.2],
        [0.2,0.8],
        [0.7,0.3],
        [0.25,0.75],
        [0.5,0.5],
        [0.1,0.9],
        ])
    print(lossF_cross_entropy(Y_true,Y_pred_p)) #torch.log默认以e为底

1.4 softmax loss及其变种

softmax loss是交叉熵损失的特例：神经网络中最后一层全连接层的输出结果其范围为(−∞,+∞)(−∞,+∞)，softmax的作用是将范围转换到0~1，此时，第i个样本对第j类的预测概率pij就可以表示为：

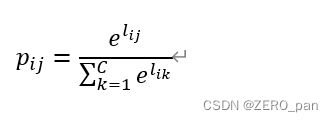
lij表示神经网络对第i个样本在第j类输出的值。

2.回归任务中的损失函数

2.1. MSE均方误差

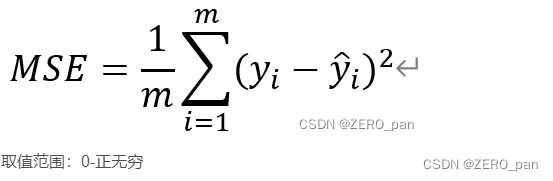
2.2. MAE

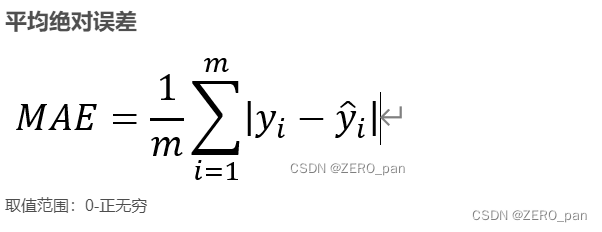
2.3.其他

其他回归任务的损失函数参考: 回归任务损失函数