LittleFOC工程简记——基于定点数的电流PI控制器设计
这里罗列了系列文章链接
前言
在FOC程序在设计的过程中,对于很多芯片而言,其缺乏浮点数运算器,因此大量的浮点数运算会给系统带来很大的计算负担。对于整个系统而言,采用定点数对整体程序进行优化,可以大幅减轻控制器的计算压力,从而实现更加理想的控制。本文针对定点数环境下的PI控制器的算法设计进行简要讨论,欢迎各位同学批评指正。
电机系统
对于大部分电机系统,其电流与电压的输入输出关系可以描述为
V ( t ) = R ∗ i ( t ) + L ∗ d i ( t ) d t V(t) = R * i(t) + L * \frac{di(t)}{dt} V(t)=R∗i(t)+L∗dtdi(t)
我们对其进行拉普拉斯变换
i ( s ) V ( s ) = 1 R + L s = 1 R 1 1 + L R s \frac{i(s)}{V(s)}= \frac{1}{ R + Ls} = \frac{1}{R} \frac{1}{ 1 +\frac{L}{R}s} V(s)i(s)=R+Ls1=R11+RLs1
可以观察到匹配到合适的电阻值时系统在大部分时间可以输出稳可控的电流,该方案仅在电机堵转的情况下是合理的。
但在实际电机运动的过程中,由于磁铁的旋转导致线圈内部磁通变化,引起反电动势的变化,从而导致电流发生波动,这一现象往往是不可预测的。考虑到实测电流决定线圈实际磁通大小,而磁力与磁通直接挂钩( F = ϕ S 2 2 μ 0 S F = \frac{\phi S^2}{2\mu_0S} F=2μ0SϕS2),而最终想要速度稳定需要保证扭矩与阻尼保持平衡。对于系统的电流控制显得尤为重要。
在FOC系统中通常采用PI控制器对电流进行闭环矫正,其结构图如下
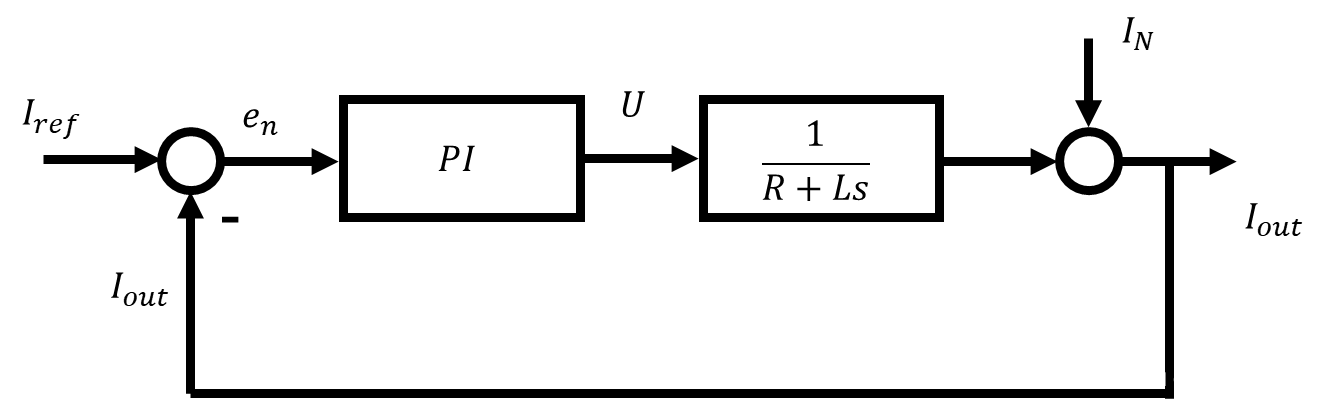
其中并联PI控制器结构图如下图所示,在这个系统中,采用串联式PI控制器调控效果会更优,其解释参考https://zhuanlan.zhihu.com/p/454914546#:,实际上此处设定 k p = k a , k i = k a ∗ k b k_p=k_a, k_i = k_a*k_b kp=ka,ki=ka∗kb即可

求其系统总体闭环传递函数,可得
G ( s ) = 1 K b s + 1 L K a K b s 2 + ( 1 K b + R K a K b ) s + 1 G(s) = \frac{\frac{1}{K_b}s+1}{\frac{L}{K_aK_b}s^2+(\frac{1}{K_b}+\frac{R}{K_aK_b})s+1} G(s)=KaKbLs2+(Kb1+KaKbR)s+1Kb1s+1
其中我们设定 1 K b ∗ R K a K b = L K a K b \frac{1}{K_b} * \frac{R}{K_aK_b} = \frac{L}{K_aK_b} Kb1∗KaKbR=KaKbL,以抵消一对极点和零点,可得 K b = R L K_b=\frac{R}{L} Kb=LR,传递函数将会被简化为
G ( s ) = 1 L K a s + 1 G(s) = \frac{1}{\frac{L}{K_a}s+1} G(s)=KaLs+11
其中 K a = B n a d w i d t h ∗ L K_a=Bnadwidth * L Ka=Bnadwidth∗L,对两个参数进行离散化与归一化,可得
{ K a = B n a d w i d t h ∗ L ∗ I b a s e U b a s e ∗ T b a s e K b = R L ∗ T s \left\{ \begin{array}{l} K_a=Bnadwidth * L * \frac{I_{base}}{U_{base}*T_{base}}\\ K_b=\frac{R}{L}*Ts \end{array} \right. {Ka=Bnadwidth∗L∗Ubase∗TbaseIbaseKb=LR∗Ts
https://blog.csdn.net/richardgann/article/details/99704448
工程分析
对于系统中的PI控制器可以用下图进行描述
对于上图的PI控制器,可以归纳出
U o u t = k p ∗ e r r o r n + k i ∗ ∑ e r r o r n Δ U o u t = ( k p + k i ) ∗ e r r o r n − k p ∗ e r r o r n − 1 \begin{array}{c} U_{out} = k_p * error_n + k_i * \sum error_n\\ \Delta U_{out} = (k_p + k_i) * error_n - k_p * error_{n-1}\\ \end{array} Uout=kp∗errorn+ki∗∑errornΔUout=(kp+ki)∗errorn−kp∗errorn−1
定义
{ k n = k p + k i k n − 1 = − k p \left\{ \begin{array}{l} k_n = k_p + k_i \\ k_{n-1} = -k_p \end{array} \right. {kn=kp+kikn−1=−kp
因此增量式PI控制器计算公式为
{ e r r o r n = I r e f − I n Δ U o u t = k n ∗ e r r o r n + k n − 1 ∗ e r r o r n − 1 U o u t = ∑ Δ U o u t \left\{ \begin{array}{l} error_n = I_{ref} - I_{n}\\ \Delta U_{out} = k_n * error_n + k_{n-1} * error_{n-1}\\ U_{out} = \sum \Delta U_{out} \end{array} \right. ⎩
⎨
⎧errorn=Iref−InΔUout=kn∗errorn+kn−1∗errorn−1Uout=∑ΔUout
考虑输入输出内容的定义域,由于各个参量都为定点数(q15_t),因此其定义域为
{ I r e f ∈ [ − 1 , 1 ) I n ∈ [ − 1 , 1 ) U o u t ∈ [ − 1 , 1 ) \left\{ \begin{array}{l} I_{ref} \in [-1, 1)\\ I_{n} \in [-1, 1)\\ U_{out} \in [-1, 1) \end{array} \right. ⎩
⎨
⎧Iref∈[−1,1)In∈[−1,1)Uout∈[−1,1)
计算过程中
{ e r r o r n ∈ ( − 2 , 2 ) Δ U o u t ∈ ( − 2 ( k n − k n − 1 ) , 2 ( k n − k n − 1 ) ) \left\{ \begin{array}{l} error_n \in (-2, 2)\\ \Delta U_{out} \in (-2(k_n-k_{n-1}), 2(k_n-k_{n-1})) \end{array} \right. {errorn∈(−2,2)ΔUout∈(−2(kn−kn−1),2(kn−kn−1))
再考虑到要保证 U o u t ∈ [ − 1 , 1 ) U_{out} \in [-1, 1) Uout∈[−1,1),显然 k n − k n − 1 = 2 ∗ k p + k i < 0.5 k_n - k_{n-1}=2 * k_p + k_i< 0.5 kn−kn−1=2∗kp+ki<0.5,因此需要控制 k p < 0.25 k_p< 0.25 kp<0.25且 k i < 0.5 k_i< 0.5 ki<0.5。
此外,由于 e r r o r n = I r e f − I n ∈ ( − 2 , 2 ) error_n = I_{ref} - I_{n} \in (-2, 2) errorn=Iref−In∈(−2,2),变量 e r r o r n error_n errorn应转变为q14_t或q_30_t格式进行计算,由于笔者采用ADC精度仅在12位,因此对输入变量从q15_t降为q14_t并不会影响其精度。
对于 Δ U o u t \Delta U_{out} ΔUout仍采用q14_t格式进行计算,设定其最大值为1,最小值为-1,这同时保证了在满足 k p < 0.25 k_p< 0.25 kp<0.25且 k i < 0.5 k_i< 0.5 ki<0.5时 Δ U o u t \Delta U_{out} ΔUout的运算不会溢出。
变量 U o u t U_{out} Uout同样采用q14_t格式进行计算,设定其最大值为1,最小值为-1,对外输出q15_t格式。
工程代码
工程代码未经过严格测试,使用前请谨慎检查
/* Define to prevent recursive inclusion -------------------------------------*/
#ifndef __PI_CONTROLLER_H
#define __PI_CONTROLLER_H
/* =================================================================================
File name: __PI_CONTROLLER_H
改编自https://blog.csdn.net/wind4study/article/details/45116281
===================================================================================*/
#ifdef __cplusplus
extern "C" {
#endif
/* Includes ------------------------------------------------------------------*/
#include "main.h"
typedef struct PI_Controller_ PI_Controller;
typedef void (*PICfptrInit)(PI_Controller*, q15_t, q15_t, q15_t, q15_t);
typedef q15_t (*PICfptrCalc)(PI_Controller*, q15_t);
struct PI_Controller_
{
q14_t kp;
q14_t ki;
q14_t limit1;
q14_t limit2;
q14_t kn;
q14_t kn_1;
q14_t setValue;
q14_t errorn_1;
q14_t delta_Un;
q14_t Un;
q15_t output;
PICfptrInit init;
PICfptrCalc calc;
};
PI_Controller* new_PI_Controller(void);
void delete_PI_Controller(PI_Controller* const pPICObj);
void PI_controller_init(PI_Controller* const pPICObj, q15_t kp, q15_t ki, q15_t limit1, q15_t limit2);
q15_t PI_controller_calc(PI_Controller* const pPICObj, q15_t value);
#endif
/* =================================================================================
File name: __PI_CONTROLLER_C
===================================================================================*/
#include "PI_controller.h"
PI_Controller* new_PI_Controller(void)
{
PI_Controller* pObj = NULL;
pObj = (PI_Controller*)malloc(sizeof(PI_Controller));
if (pObj == NULL)
{
return NULL;
}
pObj->init = PI_controller_init;
pObj->calc = PI_controller_calc;
pObj->Un = 0;
return pObj;
}
void delete_PI_Controller(PI_Controller* const pPICObj)
{
free(pPICObj);
}
void PI_controller_init(PI_Controller* const pPICObj, q15_t kp, q15_t ki, q15_t limit1, q15_t limit2)
{
pPICObj->setValue = 0;
pPICObj->kp = kp>>1;
if(pPICObj->kp > 0x0fff)
{
pPICObj->kp = 0x0fff;
printf("Warning: The value of kp is too large!\r\n");
}
pPICObj->ki = ki>>1;
if(pPICObj->ki > 0x0fff)
{
pPICObj->ki = 0x0fff;
printf("Warning: The value of ki is too large!\r\n");
}
pPICObj->kn = pPICObj->kp + pPICObj->ki;
pPICObj->kn_1 = -pPICObj->kp;
pPICObj->limit2 = limit2>>1;
if(pPICObj->limit2 > 0x3fff)
{
pPICObj->limit2 = 0x3fff;
printf("Warning: The value of limit2 is too large!\r\n");
}
pPICObj->limit1 = limit1>>1;
if(pPICObj->limit1 < -0x3fff)
{
pPICObj->limit1 = -0x3fff;
printf("Warning: The value of limit1 is too large!\r\n");
}
pPICObj->delta_Un = 0;
pPICObj->errorn_1 = 0;
}
q15_t PI_controller_calc(PI_Controller* const pPICObj, q15_t value)
{
q14_t errorn =0;
errorn = pPICObj->setValue - (value>>1);
pPICObj->delta_Un = my_mult_q14(pPICObj->kn, errorn) + my_mult_q14(pPICObj->kn_1, pPICObj->errorn_1);
pPICObj->errorn_1 = errorn;
if(pPICObj->delta_Un > 0x3fff)
pPICObj->delta_Un = 0x3fff;
else if(pPICObj->delta_Un < -0x3fff)
pPICObj->delta_Un = -0x3fff;
pPICObj->Un += pPICObj->delta_Un;
if(pPICObj->Un > pPICObj->limit2)
pPICObj->Un = pPICObj->limit2;
else if(pPICObj->Un < pPICObj->limit1)
pPICObj->Un = pPICObj->limit1;
pPICObj->output = pPICObj->Un << 1;
return pPICObj->output;
}
关于定点数的计算函数
typedef int16_t q14_t;
typedef int16_t q15_t;
q14_t my_mult_q14(q14_t SrcA, q14_t SrcB)
{
return ((int16_t)SrcA * SrcB)>>14;
}
q15_t my_mult_q15(q15_t SrcA, q15_t SrcB)
{
return ((int16_t)SrcA * SrcB)>>15;
}