模式识别中的Fisher线性判别分析
从这次博客开始将不会像以前一样将大段的《模式识别(第三版)》原文大部分内容重新说一遍,而是直接解释原文中的疑难点。一是这些文章是提供给自己或那些已经学习了但不理解部分知识点的《模式识别》读者,而不是面对那些想从看博客就学会模式识别的人;二是直接从原文摘抄既费时又多余,应该多把时间花在解释上面。
Fisher线性判别分析的基本思想
当只有两类的情况下,将多个多维的已知类别的样本投影到一个一维的向量上,在这个一维的向量上确定一个分界点。由这个分界点便可以判断出新样本的类别。可以参考下图:
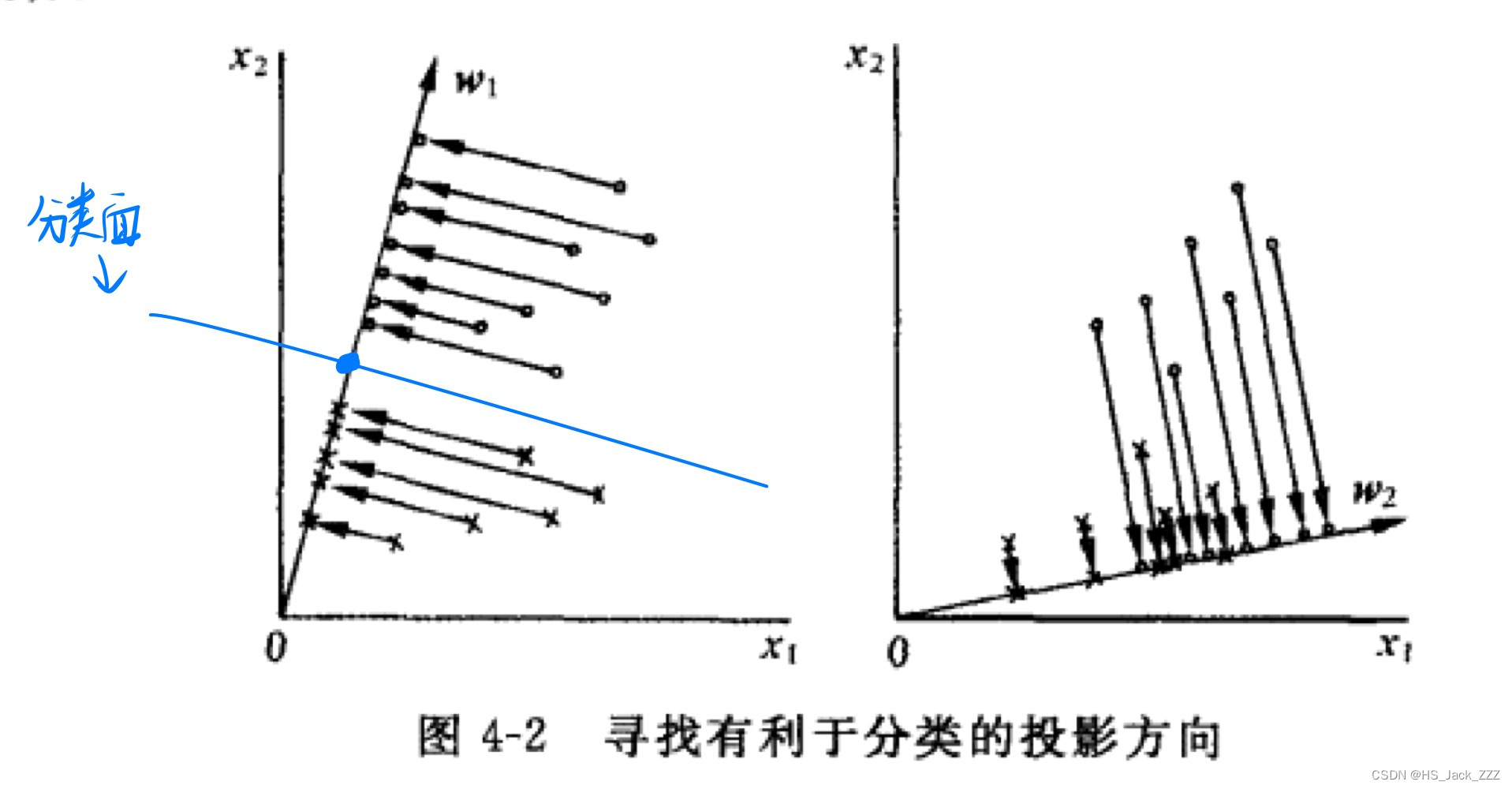
可以看到,左图就是一个很好的分类示范:同一类的样本相对集中在一起;不同一类的样本相对远离。右图是一个不好的分类示范,因为在投影之后的一维向量上不好区分出两类来。
现在的首要问题就是要找到这个一维向量使得所有投影在这个向量上的样本能区分开来。我们先研究以下这个向量:
用 w ⃗ \mathbf{\vec{w}} w表示我们要求解的向量,书本上叫它投影方向 w ⃗ \mathbf{\vec{w}} w。这个向量的长度 ∣ ∣ w ⃗ ∣ ∣ ||\mathbf{\vec{w}}|| ∣∣w∣∣我们并不关心,方向才是我们关注的重点。书中并没有指明向量 w ⃗ \mathbf{\vec{w}} w的大小(不一定是单位向量),因此投影以后的样本
y i = w ⃗ T x i ⃗ , i = 1 , 2 , . . . , N y_i=\mathbf{\vec{w}}^T\vec{x_i},~~i=1,2,...,N yi=wTxi, i=1,2,...,N
是一个相对大小的标量,与投影到的直线上的大小无关!这个标量数值其实意义不大,只有在与阈值比较大小时才有意义。
首先讨论在 d d d维空间中样本的特性:
在原样本空间中,类均值向量为
m i ⃗ = 1 N ∑ x j ⃗ ∈ X i x j ⃗ \vec{m_i}=\frac{1}{N}\sum_{\vec{x_j}\in X_i}\vec{x_j} mi=N1xj∈Xi∑xj
书本中定义各类的类内离散程度矩阵为:
S i = ∑ x j ⃗ ∈ X i ( x j ⃗ − m i ⃗ ) ( x j ⃗ − m i ⃗ ) T \mathbf{S}_i=\sum_{\vec{x_j}\in Xi}(\vec{x_j}-\vec{m_i})(\vec{x_j}-\vec{m_i})^T Si=xj∈Xi∑(xj−mi)(xj−mi)T
我愿称之为加了权的协方差矩阵。权重便是式子中的 ∑ x j ⃗ ∈ X i \sum_{\vec{x_j}\in Xi} ∑xj∈Xi,因为正常的协方差举证需要在式前乘 1 N i \frac{1}{N_i} Ni1,而这里为什么没有乘呢?是因为在求总的类内离散程度矩阵
S W = S 1 + S 2 \mathbf{S}_W=\mathbf{S}_1+\mathbf{S}_2 SW=S1+S2
时,加了权的类内协方差矩阵既可以表示在总的离散程度矩阵中该类贡献的离散程度大小。这个离散程度大小受两方面影响:一是样本间的离散程度;二是该类中样本的数量。
类间的离散度矩阵可以定义为:
S b = ( m 1 ⃗ − m 2 ⃗ ) ( m 1 ⃗ − m 2 ⃗ ) T \mathbf{S}_b=(\vec{m_1}-\vec{m_2})(\vec{m_1}-\vec{m_2})^T Sb=(m1−m2)(m1−m2)T
在投影以后的一维空间同样可以求出类间和类内的离散度矩阵,方法同式(2)(3)(4)(5),不同的是需要将式(1)代入即可。我们将投影后的矩阵上方标记~。
书本给出了Fisher准则函数为:
m a x J F ( w ) = S b 2 ~ S w 2 ~ = ( m 1 ⃗ ~ − m 2 ⃗ ~ ) 2 S 1 2 ~ + S b 2 ~ maxJ_F(w)=\frac{\tilde{\mathbf{S}_b^2}}{\tilde{\mathbf{S}_w^2}}=\frac{\tilde{(\vec{m_1}}-\tilde{\vec{m_2}})^2}{\tilde{\mathbf{S}_1^2}+\tilde{\mathbf{S}_b^2}} maxJF(w)=Sw2~Sb2~=S12~+Sb2~(m1~−m2~)2
这个式子就是为了求向量 w ⃗ \mathbf{\vec{w}} w的方向,为什么是这么定义的呢?我们想要的向量是既可以让同类的样本相对集中,离散度小即式中分母 S w 2 ~ \tilde{\mathbf{S}_w^2} Sw2~尽可能小;同时让类间区别大一点,离散度大即式中分子 S b 2 ~ \tilde{\mathbf{S}_b^2} Sb2~尽可能大。我们可以将上式继续化简为(书中有详细过程):
m a x J F ( w ⃗ ) = w ⃗ T S b w ⃗ w ⃗ T S w w ⃗ maxJ_F(\vec{\mathbf{w}})=\frac{\mathbf{\vec{w}}^T\mathbf{S}_b\mathbf{\vec{w}}}{\mathbf{\vec{w}}^T\mathbf{S_w}\mathbf{\vec{w}}} maxJF(w)=wTSwwwTSbw
求解上式可以利用朗格朗日乘子法。什么!!?你还不会拉格朗日乘子法?拉格朗日乘子法赶紧去补补吧!
中间的过程书中都有,不过需要注意的是,我们之前也提到了我们只关注向量 w ⃗ \mathbf{\vec{w}} w的方向,因此与方向无关的系数都可以省略,最终取:
w ⃗ ∗ = S w − 1 ( m 1 ⃗ − m 2 ⃗ ) \mathbf{\vec{w}}^*=\mathbf{S_w}^{-1}(\vec{m_1}-\vec{m_2}) w∗=Sw−1(m1−m2)
这就是Fisher判别函数准则下的最优投影方向。
另一种方法是式(7)对向量 w ⃗ \vec{\mathbf{w}} w求导等于0得到。注意的点也是将与方向无关的系数省略即可。
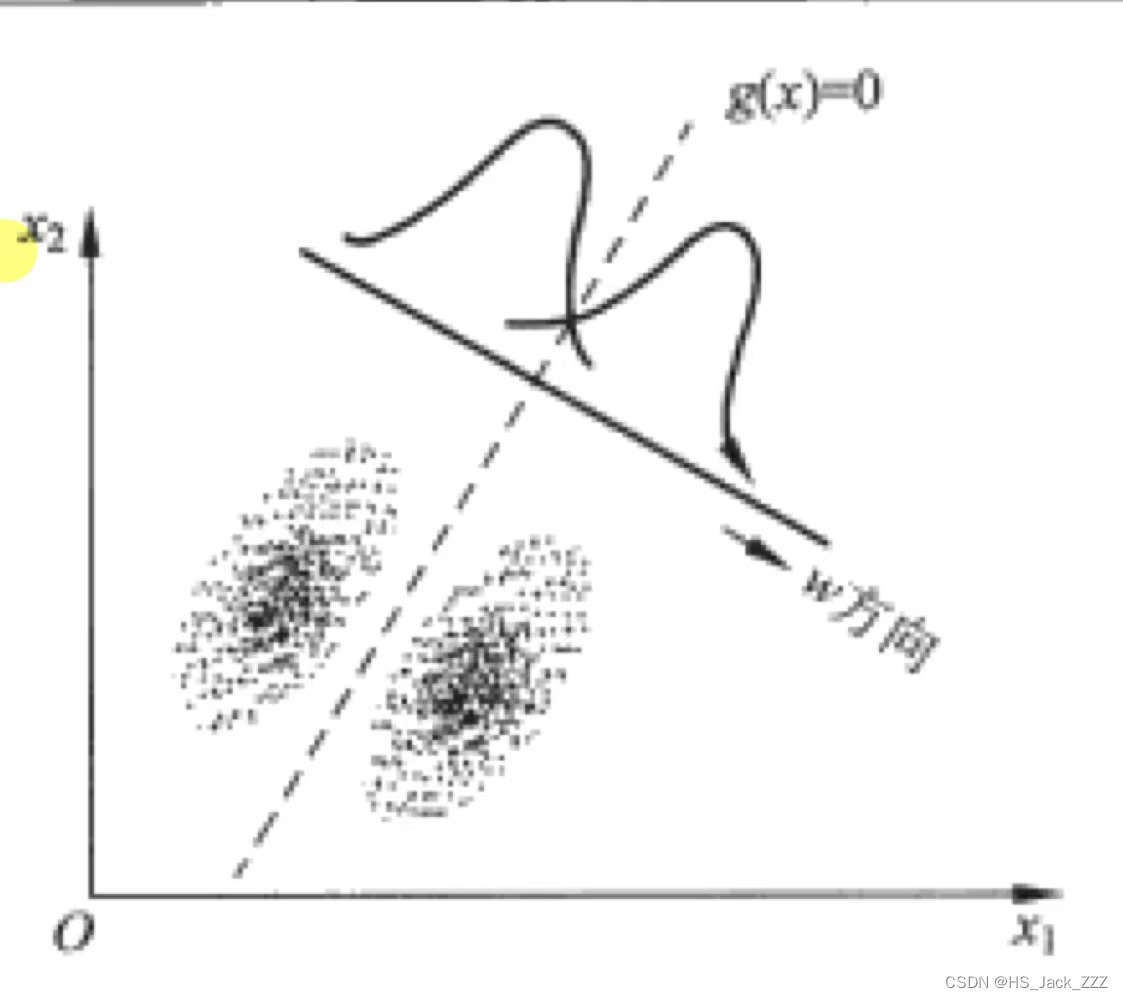
说了这么多是不是以为我们已经开始分类了?NONONO!前面那么多只是找到了一个最好的投影方向,即**Fisher判别函数最优的解本身只是给出了一个投影方向,并没有给出我们所要的分类面!**要得到分类面,需要在投影后的方向上确定一个分类阈值 w 0 w_0 w0,得到下面的决策规则:
若 g ( x ⃗ ) = w ⃗ T x ⃗ + w 0 ≷ 0 ,则 x ⃗ ∈ { w 1 w 2 若g(\vec{x})=\mathbf{\vec{w}}^T\vec{x}+w_0\gtrless0,则\vec{x}\in\left\{\begin{matrix} w_1\\ w_2 \end{matrix}\right. 若g(x)=wTx+w0≷0,则x∈{w1w2
这个式子是不是很眼熟,跟我们学的标准的线性判别函数是一样的,基本概念在这里线性判别函数基本概念可以复习的看一看。
同时,我们再回顾一下在正太分布的样本条件下且两类协方差相同的情况下(第二种情况),最优贝叶斯分类器是线性函数 g ( x ⃗ ) = w ⃗ T x ⃗ + w 0 g(\vec{x})=\mathbf{\vec{w}}^T\vec{x}+w_0 g(x)=wTx+w0,其中
w ⃗ = ∑ − 1 ( μ 1 ⃗ − μ 2 ⃗ ) \mathbf{\vec{w}}=\sum{}^{-1}(\vec{\mu_1}-\vec{\mu_2}) w=∑−1(μ1−μ2)
w 0 = − 1 2 ( μ 1 ⃗ + μ 2 ⃗ ) T ∑ − 1 ( μ 1 ⃗ − μ 2 ⃗ ) − l n p ( w 2 ) p ( w 1 ) w_0=-\frac{1}{2}(\vec{\mu_1}+\vec{\mu_2})^T\sum{}^{-1}(\vec{\mu_1}-\vec{\mu_2})-ln\frac{p(w_2)}{p(w_1)} w0=−21(μ1+μ2)T∑−1(μ1−μ2)−lnp(w1)p(w2)
比较一下式(8)和式(10),有没有感觉很相似?看不出来的话,我们放在一起比较一下:
S w − 1 ( m 1 ⃗ − m 2 ⃗ ) ∼ ∑ − 1 ( μ 1 ⃗ − μ 2 ⃗ ) \mathbf{S_w}^{-1}(\vec{m_1}-\vec{m_2})\sim\sum{}^{-1}(\vec{\mu_1}-\vec{\mu_2}) Sw−1(m1−m2)∼∑−1(μ1−μ2)
我们在之前讲过,在线性分类中我们跳过求概率密度的步骤,直接得到分类器,因此我们并不知道样本的分布。但是,自然界大部分样本分布都是正态分布的,我们不凡让样本的算术平均 m i ⃗ \vec{m_i} mi作为均值 μ i ⃗ \vec{\mu_i} μi的估计、把样本协方差矩阵 S w \mathbf{S_w} Sw当作是真实协方差矩阵的估计 ∑ \sum{} ∑。那么,我们就可以用式(14)作为分类阈值,即:
w 0 = − 1 2 ( m 1 ⃗ + m 2 ⃗ ) T S w − 1 ( m 1 ⃗ − m 2 ⃗ ) − l n p ( w 2 ) p ( w 1 ) w_0=-\frac{1}{2}(\vec{m_1}+\vec{m_2})^T\mathbf{S_w}^{-1}(\vec{m_1}-\vec{m_2})-ln\frac{p(w_2)}{p(w_1)} w0=−21(m1+m2)TSw−1(m1−m2)−lnp(w1)p(w2)
**真实的样本分布可能不是正态分布!**所以这种投影方向和阈值并不能保证是最优的,但通常仍可以取得较好的分类结果。
将式(13)代入到式(9)中就可以得到拟合为正态分布的决策规则:
若 g ( x ⃗ ) = w ⃗ T x ⃗ + − 1 2 ( m 1 ⃗ + m 2 ⃗ ) T S w − 1 ( m 1 ⃗ − m 2 ⃗ ) − l n p ( w 2 ) p ( w 1 ) ≷ 0 ,则 x ⃗ ∈ { w 1 w 2 若g(\vec{x})=\mathbf{\vec{w}}^T\vec{x}+-\frac{1}{2}(\vec{m_1}+\vec{m_2})^T\mathbf{S_w}^{-1}(\vec{m_1}-\vec{m_2})-ln\frac{p(w_2)}{p(w_1)}\gtrless0,则\vec{x}\in \left\{\begin{matrix} w_1\\ w_2 \end{matrix}\right. 若g(x)=wTx+−21(m1+m2)TSw−1(m1−m2)−lnp(w1)p(w2)≷0,则x∈{w1w2
可以进一步化简为:
若 g ( x ⃗ ) = w ⃗ T ( x ⃗ − 1 2 ( m 1 ⃗ + m 2 ⃗ ) ) ≷ l n p ( w 2 ) p ( w 1 ) ,则 x ⃗ ∈ { w 1 w 2 若g(\vec{x})=\mathbf{\vec{w}}^T(\vec{x}-\frac{1}{2}(\vec{m_1}+\vec{m_2}))\gtrless ln\frac{p(w_2)}{p(w_1)},则\vec{x}\in \left\{\begin{matrix} w_1\\ w_2 \end{matrix}\right. 若g(x)=wT(x−21(m1+m2))≷lnp(w1)p(w2),则x∈{w1w2
因为Fisher线性判别并不对样本的分布作任何假设,但在很多情况下,当样本维数较高且样本数很多时,投影到一维空间后样本接近正态分布。直观理解式(15)就是,将样本投影到一维后,将分布假设为正太分布作出分类决策。在先验概率相同时,以该平分点为两类的分解点(为什么是平分点可以去看看正太分布的决策)。先验概率不同时,分解点向先验概率小的一侧偏移。具体可以参考书本原图(下图)。