
文章目录
引言
在实际的dfs问题中,大多时候并不会直接告诉你,而是需要自己发现可以使用dfs来解决。而是否能用dfs解决的关键,就是画出决策树!同时,不同的决策树代表不同的解决方式,对于同一问题,好的决策树往往能节省时间,提高效率。
一、全排列

1. 决策树

绿色部分,就是剪枝,因为全排列不能重复枚举。
2. 设计代码
1. 全局变量
- vector<vector< int >> ret:用来保存最终所有的结果
- vector< int > path:用来保存单一路径的结果
- bool check[6]:用来实现剪枝
2. dfs函数
- 将数组中所有数枚举一遍,如果没有枚举过,则将其加入path
3. 细节问题
- 回溯
- 清除path中最后一个数
- 更改check中的标记
- 剪枝:根据check的标记,去除重复枚举的情况
- 递归出口:当path路径长度等于枚举数组长度,则将其加入ret,返回
class Solution
{
vector<vector<int>> ret;
vector<int> path;
bool check[6];//实现剪枝
public:
void dfs(vector<int>& nums)
{
if(path.size() == nums.size())
{
ret.push_back(path);
return;
}
for(int i=0; i<nums.size(); ++i)
{
if(!check[i])//剪枝
{
path.push_back(nums[i]);
check[i] = true;
dfs(nums);
//回溯 - 恢复现场
path.pop_back();
check[i] = false;
}
}
}
vector<vector<int>> permute(vector<int>& nums)
{
dfs(nums);
return ret;
}
};
二、子集

解法一
1. 决策树

2. 设计代码
1. 全局变量
- vector<vector< int >> ret:用来保存最终所有的结果
- vector< int > path:用来保存单一路径的结果
2. dfs函数
- 对于数组中的每一个数,都遵循选或不选两种方式
- 不选:直接dfs下一层
- 选:先将其加入path,再dfs下一层
- dfs(nums, i):增加参数i作为当前数的下标
3. 细节问题
- 回溯:删除path中最后一个数
- 递归出口:当i枚举完所有数,来到数组末尾,则将path加入ret,返回
class Solution
{
vector<vector<int>> ret;
vector<int> path;
public:
void dfs(vector<int>& nums, int i)
{
if(i == nums.size())
{
ret.push_back(path);
return;
}
//不选
dfs(nums, i+1);
//选
path.push_back(nums[i]);
dfs(nums, i+1);
path.pop_back();
}
vector<vector<int>> subsets(vector<int>& nums)
{
dfs(nums, 0);
return ret;
}
};
解法二
1. 决策树

由于决策树不同的选取,解法二要优于解法一
2. 设计代码
1. 全局变量
- vector<vector< int >> ret:用来保存最终所有的结果
- vector< int > path:用来保存单一路径的结果
2. dfs函数
- 按照集合中元素的个数进行分类
- 依据集合的互异性,每层dfs只能选取下标i后面的数
- dfs(nums, i):增加参数i作为当前数的下标
3. 细节问题
- 回溯:删除path中最后一个数
- 递归出口:每一层path都是结果,都需要添加到ret
class Solution
{
vector<vector<int>> ret;
vector<int> path;
public:
void dfs(vector<int>& nums, int i)
{
ret.push_back(path);
for(int j=i; j<nums.size(); ++j)
{
path.push_back(nums[j]);
dfs(nums, j+1);
path.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums)
{
dfs(nums, 0);
return ret;
}
};
三、子集的异或总和之和

思路:子集的变式题(按照集合元素个数分类)
class Solution
{
int ret = 0;
int path = 0;
public:
void dfs(vector<int>& nums, int pos)
{
ret += path;
for(int i=pos; i<nums.size(); ++i)
{
path ^= nums[i];
dfs(nums, i + 1);
path ^= nums[i];
}
}
int subsetXORSum(vector<int>& nums)
{
dfs(nums, 0);
return ret;
}
};
四、全排列 ||

思路:本题是全排列的进阶版,存在重复元素,所以剪枝是关键。
- 前提:先对数组排序
- 同一个元素只能使用一次(check)
- 对于每一个节点,相同的元素只能选一次

class Solution
{
vector<vector<int>> ret;
vector<int> path;
bool check[8];
public:
void dfs(vector<int>& nums)
{
if(path.size() == nums.size())
{
ret.push_back(path);
return;
}
for(int i=0; i<nums.size(); ++i)
{
if(!check[i] && (i == 0 || nums[i] != nums[i-1] || check[i-1]))
{
path.push_back(nums[i]);
check[i] = true;
dfs(nums);
check[i] = false;
path.pop_back();
}
}
}
vector<vector<int>> permuteUnique(vector<int>& nums)
{
sort(nums.begin(), nums.end());
dfs(nums);
return ret;
}
};
五、电话号码的字母组合

细节:用哈希表存储数字与字符串的映射关系

class Solution
{
vector<string> ret;
string path;
vector<string> hash = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public:
void dfs(string& digits, int pos)
{
if(path.size() == digits.size())
{
ret.push_back(path);
return;
}
int n = digits[pos] - '0';
string s = hash[n];
for(int i=0; i<s.size(); ++i)
{
path.push_back(s[i]);
dfs(digits, pos + 1);
path.pop_back();
}
}
vector<string> letterCombinations(string& digits)
{
if(digits.size() == 0) return ret;
dfs(digits, 0);
return ret;
}
};
六、括号生成



class Solution
{
vector<string> ret;
string path;
int n;
public:
void dfs(int left, int right)
{
if(right == n)
{
ret.push_back(path);
return;
}
if(left < n)
{
path.push_back('(');
dfs(left + 1, right);
path.pop_back();
}
if(right < left)
{
path.push_back(')');
dfs(left, right + 1);
path.pop_back();
}
}
vector<string> generateParenthesis(int _n)
{
n = _n;
dfs(0, 0);
return ret;
}
};
七、组合


class Solution
{
vector<vector<int>> ret;
vector<int> path;
int n, k;
public:
void dfs(int pos)
{
if(path.size() == k)
{
ret.push_back(path);
return;
}
for(int i=pos; i<=n; ++i)
{
path.push_back(i);
dfs(i + 1);
path.pop_back();
}
}
vector<vector<int>> combine(int _n, int _k)
{
n = _n, k = _k;
dfs(1);
return ret;
}
};
八、目标和

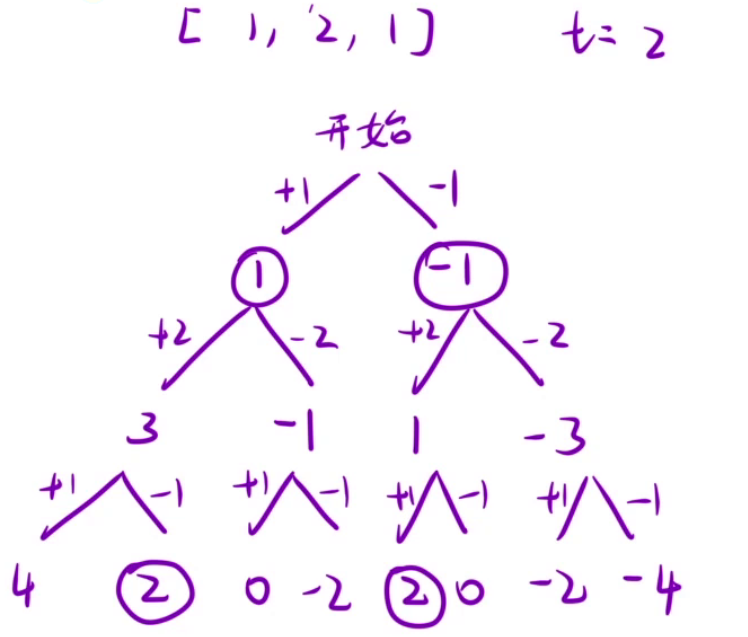
class Solution
{
int ret = 0;
int t;
public:
void dfs(vector<int>& nums, int pos, int path)
{
if(pos == nums.size())
{
if(path == t) ++ret;
return;
}
dfs(nums, pos + 1, path + nums[pos]);
dfs(nums, pos + 1, path - nums[pos]);
}
int findTargetSumWays(vector<int>& nums, int target)
{
t = target;
dfs(nums, 0, 0);
return ret;
}
};
九、组合总和


class Solution
{
vector<vector<int>> ret;
vector<int> path;
int t;
public:
void dfs(vector<int>& candidates, int pos, int sum)
{
if(sum >= t)
{
if(sum == t) ret.push_back(path);
return;
}
for(int i=pos; i<candidates.size(); ++i)
{
path.push_back(candidates[i]);
dfs(candidates, i, sum + candidates[i]);
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target)
{
t = target;
dfs(candidates, 0, 0);
return ret;
}
};
十、字母大小写全排列


class Solution
{
vector<string> ret;
public:
void dfs(string& s, int pos, string path)
{
if(path.size() == s.size())
{
ret.push_back(path);
return;
}
if(isalpha(s[pos]))
{
dfs(s, pos + 1, path + (char)tolower(s[pos]));
dfs(s, pos + 1, path + (char)toupper(s[pos]));
}
else dfs(s, pos + 1, path + s[pos]);
}
vector<string> letterCasePermutation(string& s)
{
dfs(s, 0, "");
return ret;
}
};
十一、优美的排列


class Solution
{
int ret = 0;
bool check[20];
int n;
public:
void dfs(int pos, int path)
{
if(path == n)
{
++ret;
return;
}
for(int i=1; i<=n; ++i)
{
if(!check[i] && (i % pos == 0 || pos % i == 0))
{
check[i] = true;
dfs(pos + 1, path + 1);
check[i] = false;
}
}
}
int countArrangement(int _n)
{
n = _n;
dfs(1, 0);
return ret;
}
};
总结
- 决策树
- 设计代码
- 全局变量
- dfs函数
- 细节问题
- 回溯
- 剪枝
- 递归出口
