前言
微电网将分布式电源(distributed generation,DG)与负荷组成有机整体,通过控制策略降低了分布式电源直接并网对大电网的影响,是分布式电源友好并网的有效手段。随着微电网的不断发展,局部范围内的多个微电网互相联结形成微网群,有利于微电网间的协调控制,提高整体运行稳定性和经济性。目标级联法(analytical target cascading,ATC)源于系统优化设计领域,是一种新型的、基于分解协调的、具有收敛性的协同优化方法。其基本原理是将对象系统按可行决策区间分解为由独立决策单元组成的分布式决策体系,允许各个元素自主决策,通过多轮迭代获得全局最优解,适用于层级式体系结构、仅通过连接变量耦合的问题。目标级联法近年来渐被应用在电力系统的分散调度,提供了新的分布式调度计算模式。
风光不确定模型
分布式光伏和风电的日前预测精度不高,有功出力与日前预测值的偏差在日前调度模型中应当视为不确定参数。程序通过盒式不确定集合刻画分布式光伏和风电的出力不确定性。盒式不确定集合是线性形式约束,使锥二次优化、半正定优化等原优化问题能较容易求解。
微网群两级递阶优化调度问题
下图是微网群双层联合优化的日前优化调度模型。上层模型以微网群全局层面的经济性体现,包括可控机组和储能运行成本、网群向上级配电网购电费用、网群与子微网的交易成本,其约束条件包括功率平衡约束、单元运行约束、并网功率约束,决策变量是与上级配网的联络功率、与下级子微网的联络功率、可控单元控制变量(启停机、出力值)。下层模型以子微网层面的经济性体现,包括子微网内可控单元的调控成本和网群的交易成本,其约束条件包括功率平衡约束、并网功率约束、源荷运行约束,决策变量是并网功率、可控单元控制变量(启停机、出力值)。
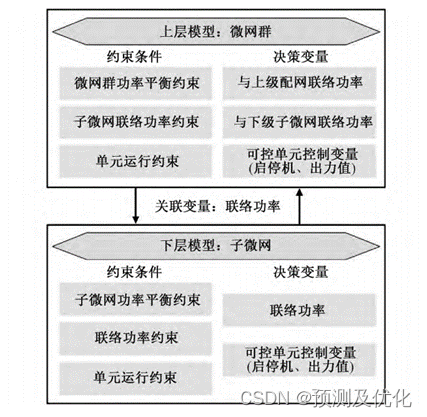
上图的微网群双层联合日前优化调度模型是控制论中的两级递阶优化问题:上层决策者首先任意给定一个决策参数(或向量),下层决策者则在该参数下,根据自己的偏好在可能范围内优化自己的目标,上层再在下层的最佳反应的基础上在可能范围内作出整体的最优决策。对于非线性问题而言,基于递阶优化思想的求解方法是:引入解耦变量,将问题转化为两个独立的单层规划问题。并将第一层问题求出的最优解来决定解耦变量如何变化,依靠分解协调原理,迭代若干步之后,求出原两级递阶优化问题最优解。这种方法通过协调以迭代方式最终实现两级递阶优化问题的求解,求解精度和速度都比较快,可解决复杂且维数较大的非线性两级递阶优化问题。常见的协调方法有:拉格朗日松弛法、交替方向乘子法、辅助问题原理法等等。
目标级联算法简介
目标级联法源于大规模复杂系统的多学科设计优化,适用于可分解为层级式目标的协调优化。目标级联法的基本思想是上层问题、下层问题分别独立求解,交叠优化,直到满足收敛条件为止。其具有并行计算、不受级数限制、经过严格收敛证明的优点。程序基于目标级联法实现对两级递阶优化问题的解耦,将上层微网群级调度问题和下层子微网级调度问题转化为独立的混合整数二次规划问题(mixed integer quadratic programming,MIQP)求解,不仅实现问题的协调求解,还实现问题的并行计算。求解步骤如下:
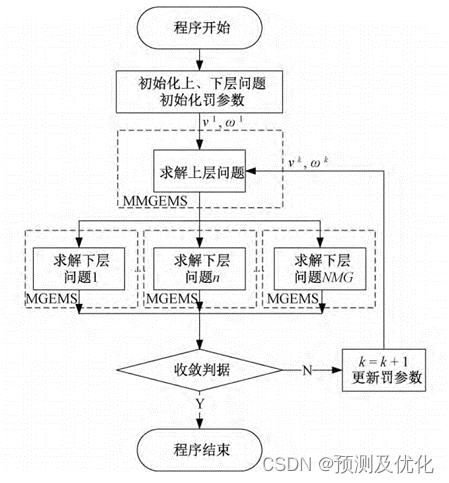
程序介绍
为提高微网群对可再生能源的接纳能力,程序考虑含多源异质分布式电源的出力随机性,采用盒式不确定集合描述不确定性,考虑最坏情况对不确定约束凸转换。建立微网群系统的两级递阶优化调度模型:上层是微网群能量调度中心优化调度模型,下层是子微网优化调度模型。对所建递阶优化调度模型的耦合性和分布性进行分析,采用一种新型的协同优化方法—目标级联法,实现上下层模型的解耦独立优化。该方法具有良好收敛和计算快速的特点,并减少数据报送,保证通信私密性。程序以含3子微网的微网群拓扑结构验证本文所提的分层分布式求解算法的有效性。该微网群具备两类利益主体:其一是微网群能量调度中心,调度中心作为运营主体也包含若干分布式电源的调控权:其二是子微网用户,其包含多类异质可再生发电单元和受控制负荷。程序中算例丰富,注释清晰,干货满满,创新性和可扩展性很高,足以撑起一篇高水平论文!下面对程序做简要介绍!
程序适用平台:Matlab+Yalmip+Cplex
参考文献:《基于目标级联法的微网群多主体分布式优化调度》-华北电力学报;
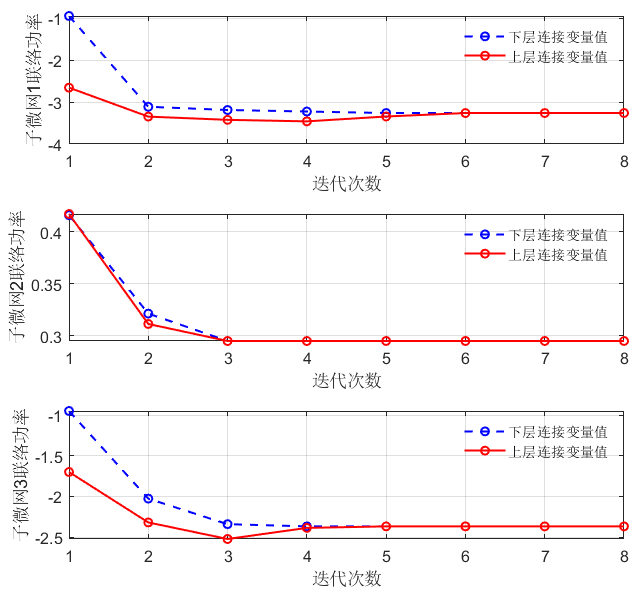
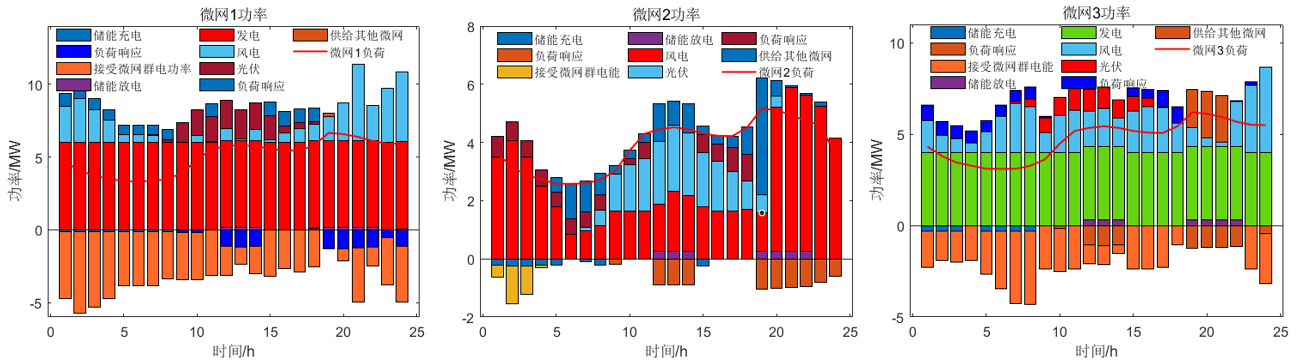
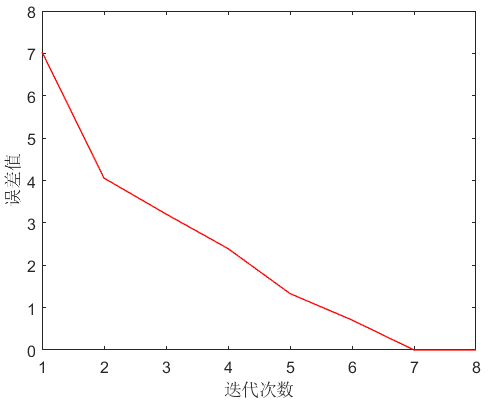
程序结果
部分程序
function cons = getConsEES(x_P_ch, x_P_dis, x_u_ch, x_u_dis, EESmax, EESmin, capmax, capmin, num_chmax, num_dismax, re, Horizon)
cons = [];
% 1. 充放电功率约束,充电记为正数,放电记为负数
cons = [cons, x_u_ch.*repmat(EESmin, 1, Horizon) <= x_P_ch <= x_u_ch.*repmat(EESmax, 1, Horizon)];
cons = [cons, - x_u_dis.*repmat(EESmax, 1, Horizon) <= x_P_dis <= - x_u_dis.*repmat(EESmin, 1, Horizon)];
% 2. 充放电次数约束
cons = [cons, sum(x_u_ch, 2) <= num_chmax];
cons = [cons, sum(x_u_dis, 2) <= num_dismax];
% 3. 不同时充放电约束
cons = [cons, 0 <= x_u_ch + x_u_dis <= 1];
% 4. SOC约束
cons = [cons, 0 <= sum(x_P_ch(:,1:ii) + x_P_dis(:,1:ii),2) <= capmax - capmin];
% 5. 爬坡约束
cons = [cons, abs([x_P_ch(:, 2:end),x_P_ch(:, 1)] - x_P_ch)<=repmat(re.*EESmax,1,Horizon)];
cons = [cons, abs([x_P_dis(:, 2:end),x_P_dis(:, 1)] - x_P_dis)<=repmat(re.*EESmax,1,Horizon)];部分内容源自网络,侵权联系删除!
欢迎感兴趣的小伙伴关注并私信获取完整版代码,小编会不定期更新高质量的学习资料、文章和程序代码,为您的科研加油助力!