重点内容：
绪论：
简单的递推方程求解 1.19(1)(2) 、 教材例题
多个函数按照阶的大小排序 1.18
分治法：
分治法解决芯片测试问题
计算a^n的复杂度为logn的算法（快速幂）
分治法解决平面最近点对问题 （增加预处理）
锦标赛算法求第二大数的步骤（链表）
分治法S中第k小元素的归约过程 （m*）
动态规划：
最长公共子序列问题：蛮力法和动态规划的递归方程或递推关系、动态规划的伪码(填空)、优化函数和标记函数(填空)
矩阵链的乘法问题 ： 蛮力法和动态规划的递归方程或递推关系、动态规划的伪码(填空)、备忘录和标记函数(填空)
最大子段和
贪心法：4.3 4.4 4.16 4.21
主要设计思想、伪码、复杂度、实例求解
贪心法：活动安排问题问题实例求解、最小延迟调度问题实例求解
回溯：
(填空)回溯算法的主要设计步骤，用回溯算法解决图的m着色问题、货郎问题(TSP)
(填空)分支界限的基本下，用分支界限算法解决最大团问题、背包问题
绪论：
多个函数按照阶的大小排序
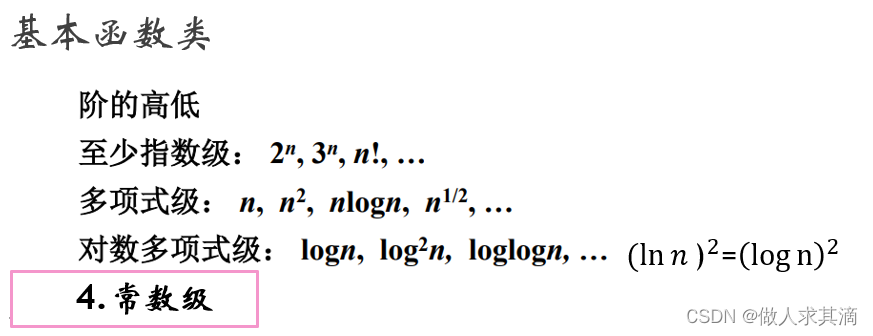
简单的递推方程求解
大小关系：指数级>多项式级>对数多项式级>常数级
化简：
主定理
https://www.bilibili.com/video/BV1Ls411W7PB/?p=16&share_source=copy_web&vd_source=7ffbd7feaeedb3d59fb21e59435a53d8教材例题
分治法：
分治法解决芯片测试问题
问题描述
一次测试过程：
两片都是好结果，就留一片。其他情况全丢掉
蛮力算法
蛮力算法的判断好坏标准（一片芯片怎么判断好坏）
n为奇数情况
n为偶数情况
结论还是不变
分治法
假设 n为偶数，将 n片芯片两两一组做 测试淘汰，剩下芯片构成子问题，进 入下一轮分组淘汰。（类似锦标赛）
分治命题正确性
主定理第三种情况ヽ(ー_ー)ノ直接记吧
计算a^n的复杂度为logn的算法（快速幂）
迭代伪码
输入：底数a，指数n
输出：计算完成的结果result
result=1； //用于存储结果
while p不为0时 do
if p为奇数
result =result *n //奇数需多乘一次底数
n=n*n；
p/=2;
递归伪码
输入：底数a，指数exponent
输出：计算完成的结果
function fastpow(a, exponent):
if exponent == 0
then return 1
if exponent == 1
then return a
temporary <- fastpow(a, exponent/2)
if exponent % 2 == 0
then return (temporary * temporary)
else
return (temporary * temporary * a)
时间复杂度
分治法解决平面最近点对问题 （增加预处理）
伪码
未改进算法时间复杂度
锦标赛算法求第二大数的步骤（链表）
分治法S中第k小元素的归约过程 （m*）
动态规划：
最长公共子序列问题：
蛮力法的时间复杂度O(n*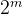
)
#include <iostream>
#include <string>
using namespace std;
string lcs_bruteforce(const string& X, const string& Y) {
int m = X.length();
int n = Y.length();
if (m == 0 || n == 0) {
return "";
} else if (X[m-1] == Y[n-1]) {
return lcs_bruteforce(X.substr(0, m-1), Y.substr(0, n-1)) + X[m-1];
} else {
string lcs1 = lcs_bruteforce(X.substr(0, m-1), Y);
string lcs2 = lcs_bruteforce(X, Y.substr(0, n-1));
if (lcs1.length() > lcs2.length()) {
return lcs1;
} else {
return lcs2;
}
}
}
int main() {
string X = "ABCBDAB";
string Y = "BDCAB";
string lcs = lcs_bruteforce(X, Y);
cout << "The longest common subsequence is: " << lcs << endl;
return 0;
}参考代码
动态规划的递归方程或递推关系
✨代码实现：
动态规划的伪码(填空)
优化函数(填空)
X = 【1, 2, 3】, Y = 【1, 3】按照下图关系推
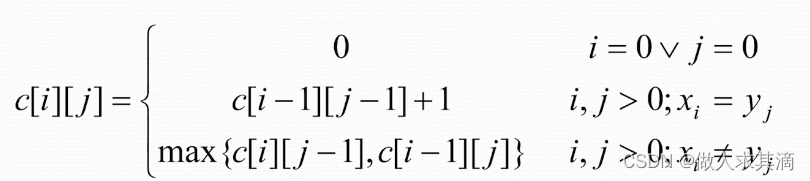
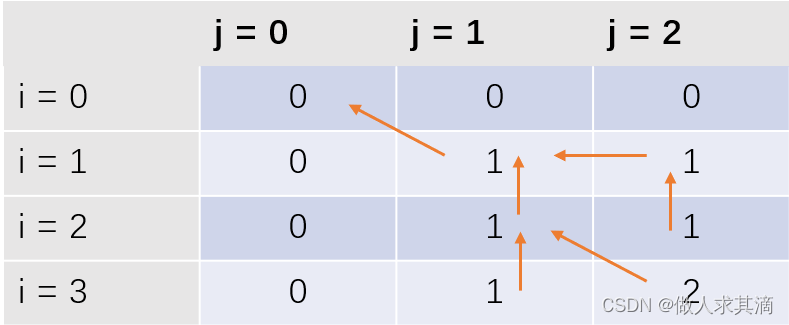
标记函数(填空)
b数组用来设立标记，算法结束后可以利用这些标记追踪最优解。
例子：
怎么推？
c[i][j]矩阵:
按照信息表即可推出b矩阵（数组）
如何追踪解？
b[i][j]为1时，对应X、Y序列第i行，j列中的元素
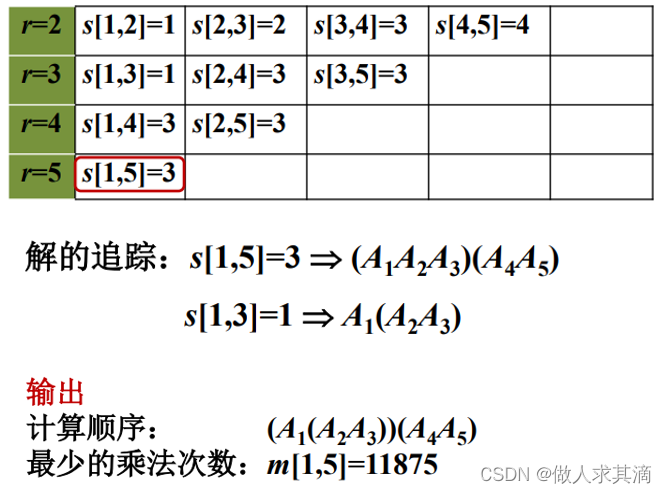
矩阵链的乘法问题：
蛮力法的时间复杂度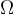
(
)
动态规划的递归方程或递推关系
动态规划的伪码(填空)
递归实现：
时间复杂度
迭代实现：
备忘录(填空)
看着递推方程来填空
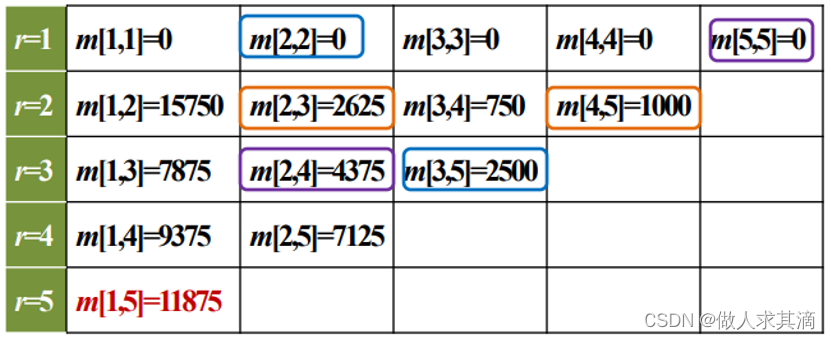
自己复制代码，断点调试设置变量查看吧
#include <bits/stdc++.h>
using namespace std;
//输入：矩阵链Ai…j的输入为向量P=<Pi-1,Pi,…,Pj>，其中：1<=i<=j<=n.
//输出：计算Ai…j的所需最小乘法运算次数m[i,j]和最后一次运算位置s[i,j]。
const int N = 101;
int m[N][N], s[N][N];
int a[] = {30, 35, 15, 5, 10, 20};
void MatrixChain(int a[N], int n)
{
for(int i=1; i<=n; i++)
m[i][i] = 0;
for(int r=2; r<=n; r++)
{
for(int i=1; i<= n-r+1; i++)
{
int j = i+r-1;
m[i][j] = m[i+1][j] + a[i-1]*a[i]*a[j];
s[i][j] = i;
for(int k=i; k<=j-1; k++)
{
int t = m[i][k] + m[k+1][j] + a[i-1]*a[k]*a[j];
if(t < m[i][j])
{
m[i][j] = t;
s[i][j] = k;
}
}
}
}
}
int main()
{
MatrixChain(a, 6);
cout << "The number of least multiplication operations:" << endl;
cout << m[1][5] << endl;
cout << "Position of the last operation:" << endl;
cout << s[1][5] << endl;
cout << "array s:" << endl;
for(int i=1; i<=5; i++)
{
for(int j=1; j<=5; j++)
{
cout << s[i][j] << ' ';
}
cout << endl;
}
return 0;
}标记函数(填空)
记录k的值，k就是分割线
