在本篇博客中将简单介绍常见的几种循环神经网络和一维卷积神经网络,并使用一些简答的数据进行拟合分析。本文相对适合刚入门的同学,同时也作为自己过去一段时间学习的总结和记录,现在神经网络框架已经非常完善的支持了很多常见和有效的深度学习算子,我们只需要掌握函数的用法就可以快速应用到自己项目中,当然希望热爱AI的同学能持续学习每一行API背后的数学逻辑和工程优化方法
认识背景
在多数工程科学和基础科学研究中都会产生大量分布的时间序列数据。在几十年前的传统的分析过程中工程师和学术界喜欢基于数值分析的过程来对模型进行建模,得到一个和对象尽可能拟合的结果。但是深度学习技术的出现使得时间序列数据的分析得到了更加简便的表达。作为新时代的研究人员有必要学习和理解几种常用的时间序列数据分析方法。
首先我们需要认识什么是时间序列数据:
最常见的例子就是语言文本,在你读到现在这句话的时候,你的认识过程中已经默认产生了对这句话的词组及其前后文的联系。如果我把上一句话改为:“读到语言文本例子最常见的,在这句话在的时候…”很明显,即使是完全相同的词汇组成的句子,随机打乱之后基本丧失了原来的含义,再或者我可以改为:“最常见的xx就是xxxx,在x读到xx这句话的xx”,那么在保持词汇顺序的前提下丢失部分词汇也无法得到原来的语义信息。
根据上面的两个例子,我们不难得知,在时间序列数据中最关注的就是这两个信息:1、每个点的数据内容;2、数据内容之间的前后文关系。这两个条件缺一不可。那么我们如何来拟合这两组数据,或者换句话说让计算机能够像人一样理解数据和数据前后关系,实现学习数据并应用在未来预测上。
在下面的曲线中,x轴作为时间数据,y轴作为时间点的目标数据,我们完全可以使用一个函数 F ( x ) \ F(x) F(x)来拟合随机分布,传统方法中有很多算法在做这件事情,在很多特殊场景下这种基于建模的传统拟合方法依然能得到非常好的结果。
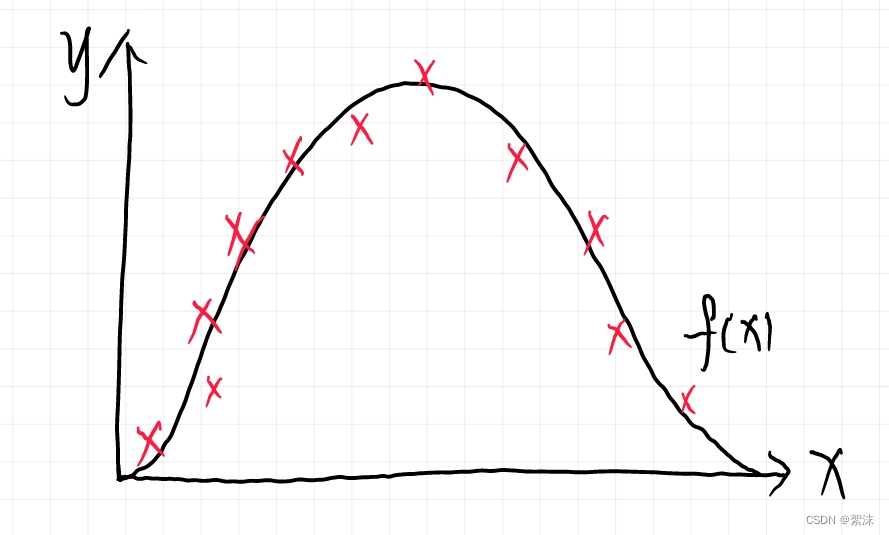
但是,并非所有的场景都局限于某一个条件之下。应该说绝大部分时间数据都包含了很多的噪声数据和复杂的非线性特征,对于神经网络来说,神经网络天然就具有良好的噪声去除能力,同时基于网络连接的系统对输入的局部数字浮动也存在较好的适应能力。
那么背景介绍的差不多了,我们直接看一下神经网络针对时间数据有些什么方法:
一维卷积神经网络
有过图像开发经验的同学应该很熟悉卷积神经网络,在常见的目标检测算法中我们使用二维卷积网络提取特征。那么,我们现在抽象一点,将一张二维的平面图像数据按照行的方向,延展为一个一维行数据。现在我们针对这个一维的图像数据就可以通过一维的卷积核来对其进行特征提取和特征压缩。
这个压缩的操作有一个专有APIlayers.Flatten()
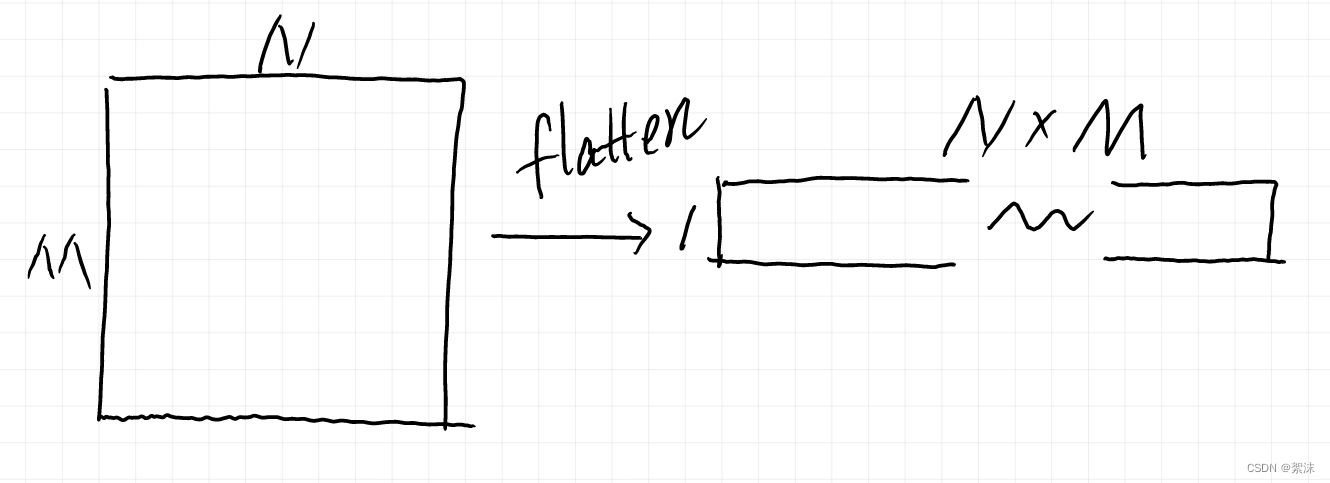
得到一维结构的数据后,我们同样可以使用卷积核来计算,只不过这个卷积核的其中一个维度是1。下面的草图里我们简单举一个15大小的卷积核,原始数据长度为H,这个卷积核依次从前向后按照步长为1滑动,每次卷积计算得到一个数值,当滑动到数据最末端的时候会得到一组长度为1(H-5)长度的映射图数据。
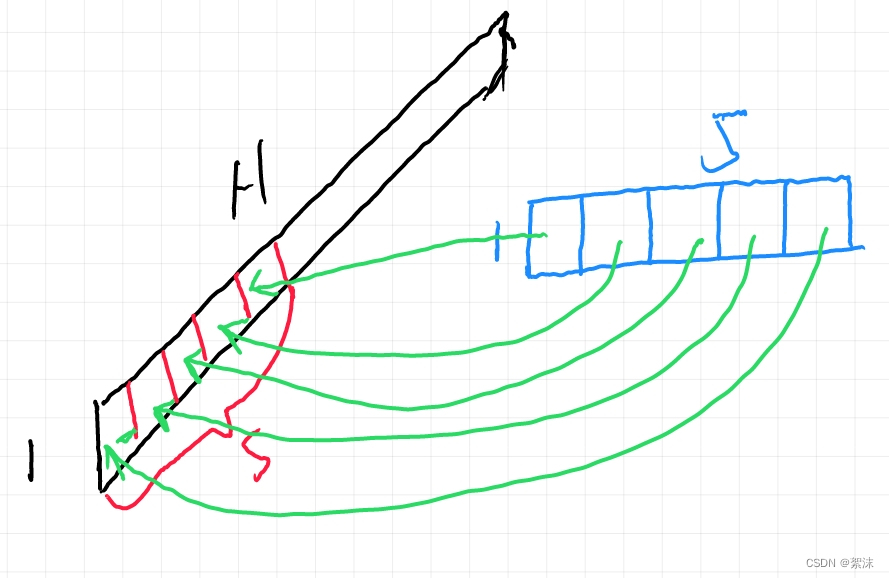
在一个卷积的基础上,我们可以调整卷积核的长度,调整卷积核的个数,达到多个同尺寸卷积核计算得到多个特征图,然后特征图再继续级联计算,多层计算之后就可以得到最终结果的输出。通过控制输出的格式我们可以实现一列数据的分类任务或者一列数据到另一列数据的映射。
一维卷积
要实现一维的卷积算法的本质还是在做矩阵运算,不同于常见的标准卷积计算,一维卷积适合来计算时间序列数据或者一维的采样数据,但是和RNN不同的是一维卷积更多的是学习数据源到目标的映射关系,RNN则同是关注数据的前后依赖,二者在不同的场景下根据源数据的特征单独使用或者组合使用。
划窗法:
考虑到一维卷积的数据计算特征——通过将源数据变换成一个第一维度为1的列或行形状矩阵,然后通过一个卷积块矢量相乘(源数据的叉乘矩阵),迭代该叉乘矩阵的内部参数和输出部分的激活函数权重,计算网络的损失值,知道得到最小化损失。
为了匹配计算过程最基础的卷积计算操作,我们有两种方式可以实现,第一种是划窗:
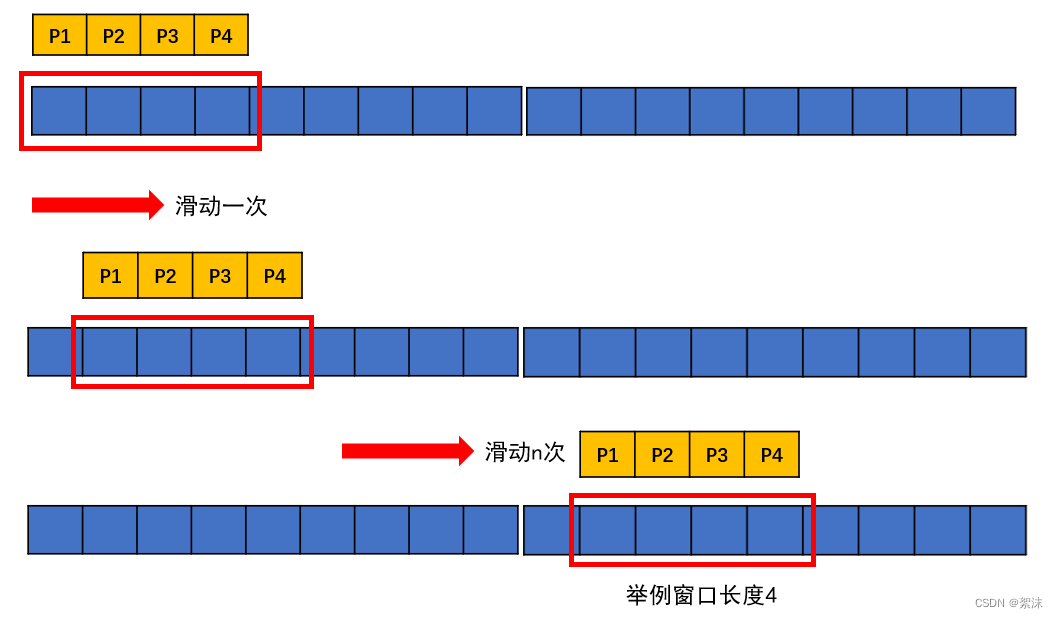
用一个固定长度的窗口按照顺序或者其它既定的规则滑动,并用一个和这个窗口相同维度的卷积核和窗口截取出来的数据做矩阵向量乘法。
分组卷积法:
在一维的向量计算过程中除了用划窗的方法截取出数据用来计算,同样还可以将原始的数据直接分组,通过分组的方式将原始数据对齐成为N-1组长度对齐的数据,然后依次的输入数据用卷积核计算
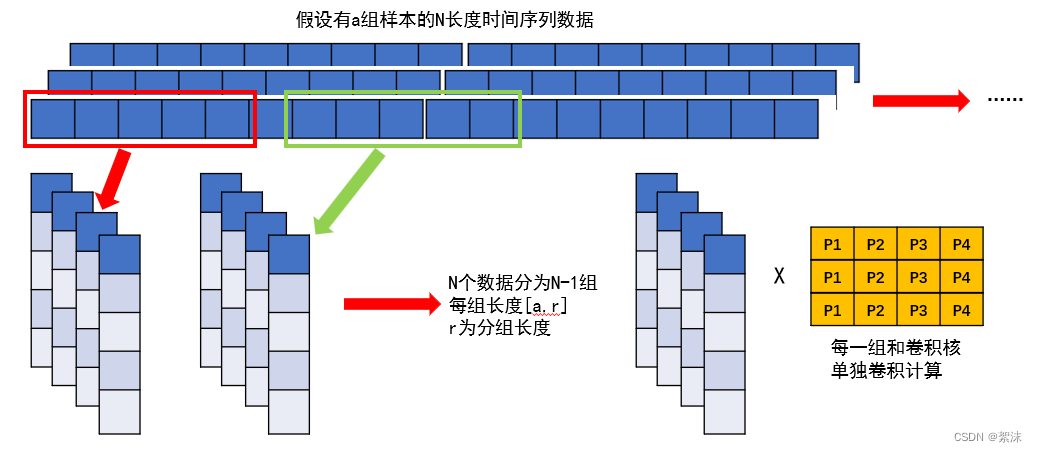
数据分组的代码实现
那继续使用一段简单的代码演示一下两种不同操作及其对应实现。在示例的代码中结合上面两者共同的优势,通过划窗顺序的选择数据,然后再通过分组将数据形成N对1的结构,实现固定长度时间序列数据输入到下一个时间点的预测学习。
import os
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.layers import Dropout, Dense, LSTM, Conv1D
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
csv_data = pd.read_csv('../Data/SH600519.csv') # 读文件数据
# soc_csv = pd.read_csv('../Data/soc.csv') # 读文件数据
test_data_rate = 0.8
training_set = csv_data['close']
test_set = training_set[int(len(training_set)*(1-test_data_rate)):]
training_set, test_set = np.array(training_set), np.array(test_set)
# 归一化
sc = MinMaxScaler(feature_range=(0, 1)) # 定义归一化:归一化到(0,1)之间
training_set_scaled = sc.fit_transform(training_set.reshape(-1, 1)) # 求得训练集的最大值,最小值这些训练集固有的属性,并在训练集上进行归一化
test_set = sc.transform(test_set.reshape(-1, 1)) # 利用训练集的属性对测试集进行归一化
处理好原数数据到可以使用了后我们就可以按照我们希望的想法对数据进行分组操作了,需要注意的一个点是,神经网络模型是对输入数据尺寸敏感的,我们在确定数据分组长度和分组后数据张量的尺度时需要同时考虑网络的卷积核大小以及训练标签数据的维度,只有这几次参数同时对齐了之后网络才可以正确初始化以及开始推理。
x_train = []
y_train = []
x_test = []
y_test = []
Time_expansion_step = 60
training_data = training_set_scaled[len(training_set_scaled)- int(len(training_set_scaled)/Time_expansion_step)
*Time_expansion_step : , :]
test_set = test_set[len(test_set)- int(len(test_set)/Time_expansion_step)
*Time_expansion_step : , :]
for i in range(Time_expansion_step, len(training_data)):
train_ = training_data[i - Time_expansion_step:i, 0]
x_train.append(train_)
y_train.append(training_data[i, 0])
# 对训练集进行打乱
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 将训练集由list格式变为array格式
x_train, y_train = np.array(x_train), np.array(y_train)
x_train = np.reshape(x_train, (x_train.shape[0], Time_expansion_step, 1))
# 设置测试数据格式
for i in range(Time_expansion_step, len(test_set)):
x_test.append(test_set[i - Time_expansion_step:i, 0])
y_test.append(test_set[i, 0])
x_test, y_test = np.array(x_test), np.array(y_test)
x_test = np.reshape(x_test, (x_test.shape[0], Time_expansion_step, 1))
代码实现
当解决了原始数据的格式之后,就是定义网络结构,并利用API实现一维数据的计算。
1、导入必要的库
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv1D, MaxPooling1D, Flatten, Dense
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.losses import SparseCategoricalCrossentropy
from tensorflow.keras.metrics import SparseCategoricalAccuracy
from tensorflow.keras.callbacks import Callback
2、生成对应格式的数据定义网络结构
# 假设我们有1000个样本,每个样本是长度为1000的时间序列,有5个不同的数值
num_samples = 100
timesteps = 1000
num_classes = 5
# 生成随机时间序列数据和标签
X = np.random.randn(num_samples, timesteps, 1)
y = np.random.randint(num_classes, size=num_samples)
print(X.shape, y.shape)
print(y[0:20])
# 构建1D CNN模型
model = Sequential([
Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(timesteps, 1)),
MaxPooling1D(pool_size=2),
Flatten(),
Dense(100, activation='relu'),
Dense(num_classes, activation='softmax')
])
打印出数据组成:
X=(100, 1000, 1) Y=(100,)
y的前20个数据内容:[1 2 2 3 3 3 1 4 2 0 0 1 0 2 4 4 2 0 2 1]
3、确定数据尺寸之后,编译模型且定义回调函数打印网络结构
# 自定义回调函数来打印每层的输入输出维度
class LayerDimensionCallback(Callback):
def on_epoch_end(self, epoch, logs=None):
print(f"Epoch {epoch+1} dimensions:")
for layer in self.model.layers:
print(f"{layer.name} - Input shape: {layer.input_shape}, Output shape: {layer.output_shape}")
# 编译模型
model.compile(optimizer=Adam(),
loss=SparseCategoricalCrossentropy(),
metrics=[SparseCategoricalAccuracy()])
print(model.summary())
打印网络的结构:
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv1d_4 (Conv1D) (None, 98, 64) 256
_________________________________________________________________
max_pooling1d_4 (MaxPooling1 (None, 49, 64) 0
_________________________________________________________________
flatten_4 (Flatten) (None, 3136) 0
_________________________________________________________________
dense_8 (Dense) (None, 100) 313700
_________________________________________________________________
dense_9 (Dense) (None, 5) 505
=================================================================
定义网络的输入为Conv1D,第二层为最大值池化,然后使用flatten将多维的数据压缩为1维的序列值,压平后的数据才可以通过全连接dense层输出
4、开始网络训练
# 训练模型并使用自定义回调函数
model.fit(X, y, epochs=10, batch_size=32, validation_split=0.2, callbacks=[LayerDimensionCallback()])
# 评估模型
loss, accuracy = model.evaluate(X, y)
print(f'Loss: {loss}, Accuracy: {accuracy}')
可以看到网络训练过程中每个层的数据尺度变化:
conv1d_4 - Input shape: (None, 100, 1), Output shape: (None, 98, 64)
max_pooling1d_4 - Input shape: (None, 98, 64), Output shape: (None, 49, 64)
flatten_4 - Input shape: (None, 49, 64), Output shape: (None, 3136)
dense_8 - Input shape: (None, 3136), Output shape: (None, 100)
dense_9 - Input shape: (None, 100), Output shape: (None, 5)
上述源代码仓库Gitee
RNN和LSTM
CNN-LSTM
CNN-LSTM的代码实现如果有同学需要可以私信,后续再继续更新
生活的惊喜总是和意外一同到来,既然很难做到事事顺心,那就主动适应环境。力求把自己该做的事做到最好。
每当和同门朋友聊起深度学习,我总是很有的兴致的那个,我想这个技术未来不久应该是一个切实改变我们生活的手段,也许GPT的成功也是历史发展上一个必然出现的节点。不过未来为了工作,或许很长时间不会再学习和更新神经网络相关的博客了。希望换个方向也能做出一番属于自己的天地。