【数学】什么是傅里叶级数与傅里叶变换？

傅里叶级数与傅里叶变换

背景

傅里叶级数和傅里叶变换是数学和工程领域中的重要工具，特别是在信号处理、图像处理和物理学中。傅里叶级数用于将周期函数表示为正弦和余弦函数的和，而傅里叶变换用于将任意函数表示为频率的函数。

公式

• 傅里叶级数：给定周期函数 $f(t)$，其傅里叶级数表示为：
  $$f(t)=a_0+\sum _{n=1}^{\infty }\left(a_n\cos \left(\frac{2\pi nt}{T}\right)+b_n\sin \left(\frac{2\pi nt}{T}\right)\right)$$
  其中：
  $$a_0=\frac{1}{T}{\int }_0^{T}f(t)dt$$
  $$a_n=\frac{2}{T}{\int }_0^{T}f(t)\cos \left(\frac{2\pi nt}{T}\right)dt$$
  $$b_n=\frac{2}{T}{\int }_0^{T}f(t)\sin \left(\frac{2\pi nt}{T}\right)dt$$

• 傅里叶变换：给定函数 $f(t)$，其傅里叶变换表示为：
  $$\mathcal{F}(f)(\omega )=F(\omega )={\int }_{-\infty }^{\infty }f(t)e^{-i\omega t}dt$$
  其逆变换为：
  $$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(\omega )e^{i\omega t}d\omega$$

示例题目

题目：求周期函数 $f(t)=t$ 在区间 $[-\pi ,\pi ]$ 上的傅里叶级数表示。

详细讲解

1. 计算 $a_0$：
   $$a_0=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }tdt=0$$
2. 计算 $a_n$：
   $$a_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }t\cos (nt)dt=0$$
3. 计算 $b_n$：
   $$b_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }t\sin (nt)dt=\frac{2(-1{)}^{n+1}}{n}$$

因此，傅里叶级数为：
$$f(t)=\sum _{n=1}^{\infty }\frac{2(-1{)}^{n+1}}{n}\sin (nt)$$

Python代码求解

import numpy as np
import matplotlib.pyplot as plt

# 定义周期函数
def f(t):
    return t

# 定义傅里叶级数展开的项数
N = 10

# 定义傅里叶级数
def fourier_series(t, N):
    result = np.zeros_like(t)
    for n in range(1, N + 1):
        result += (2 * (-1)**(n + 1) / n) * np.sin(n * t)
    return result

# 生成时间点
t = np.linspace(-np.pi, np.pi, 1000)

# 计算傅里叶级数近似
f_approx = fourier_series(t, N)

# 绘图
plt.plot(t, f(t), label='Original function')
plt.plot(t, f_approx, label='Fourier series approximation')
plt.legend()
plt.xlabel('t')
plt.ylabel('f(t)')
plt.title('Fourier Series Approximation')
plt.grid(True)
plt.show()

实际生活中的例子

在实际生活中，傅里叶变换用于信号处理，例如将音频信号转换为频谱，以分析不同频率的声音成分。傅里叶级数则在分析周期信号（如振动和电波）时非常有用。通过将复杂的周期信号分解为简单的正弦和余弦分量，可以更容易地理解和处理这些信号。

一个python例子

import numpy as np
import matplotlib.pyplot as plt

# 定义周期函数的频率和系数
T = 2 * np.pi  # 周期
N = 5  # 傅里叶级数的项数

# 定义时间范围
t = np.linspace(-np.pi, np.pi, 1000)

# 定义傅里叶级数的各项
def fourier_series_terms(t, N):
    terms = []
    for n in range(1, N + 1):
        term = (2 * (-1)**(n + 1) / n) * np.sin(n * t)
        terms.append(term)
    return terms

# 计算傅里叶级数的各项
terms = fourier_series_terms(t, N)

# 绘图
plt.figure(figsize=(12, 8))

# 原始函数
plt.subplot(2, 1, 1)
plt.plot(t, t, label='Original function')
plt.title('Original Function')
plt.xlabel('t')
plt.ylabel('f(t)')
plt.legend()
plt.grid(True)

# 各项的和
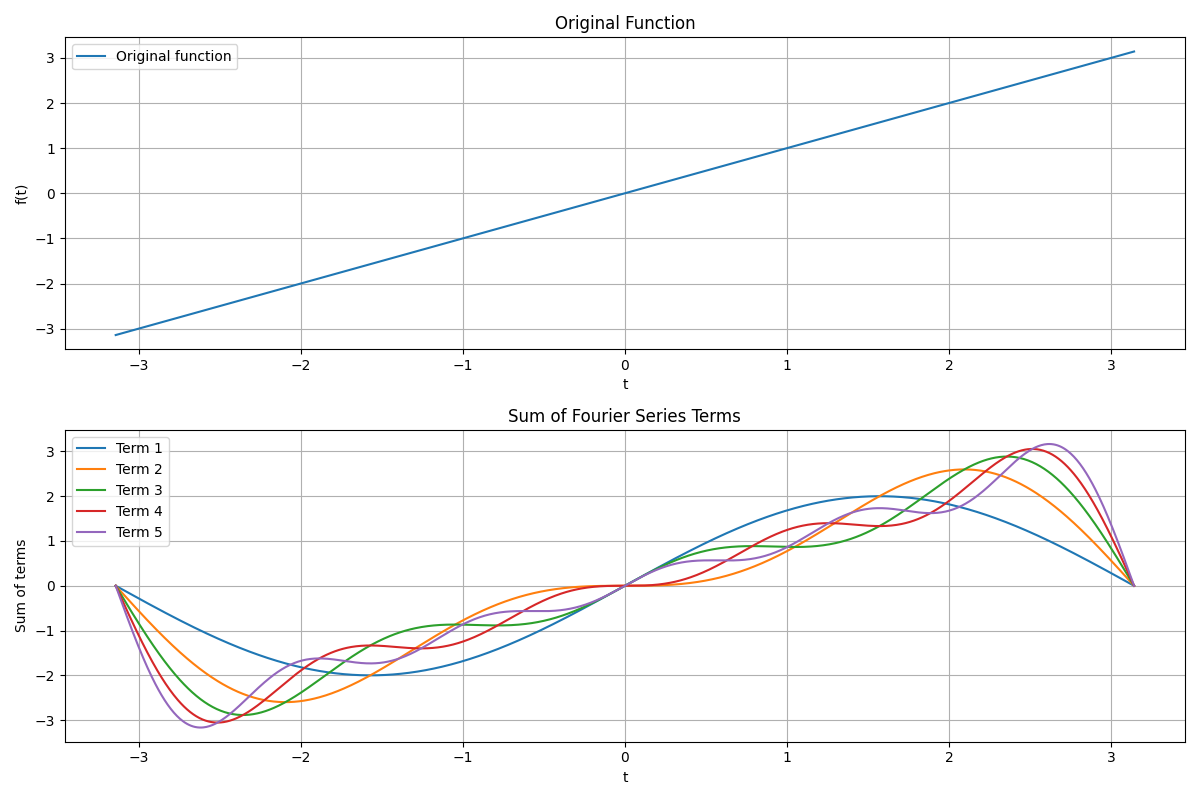
plt.subplot(2, 1, 2)
sum_terms = np.zeros_like(t)
for i, term in enumerate(terms):
    sum_terms += term
    plt.plot(t, sum_terms, label=f'Term {i+1}')
plt.title('Sum of Fourier Series Terms')
plt.xlabel('t')
plt.ylabel('Sum of terms')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()