数据结构——

1. 什么是并查集？

在计算机科学中，并查集（英文：Disjoint-set data structure，直译为不数据结构交集）是一种数据结构，用于处理一些不交集（Disjoint sets，一系列没有重复元素的集合）的合并及查询问题。

举个简单的例子

一个组织里来个10个新人，它们的编号为从1~10，假设此时它们根据彼此的老家而互相亲近（即形成一个小团体），我们要将这10个人划分成不同的小团体，这样划分后形成的结果就是并查集。

接下来我们就来模拟这10个人的划分过程，首先我们可以将每个人的初始值设置为-1，当两个人都属于同一个小团体时，将其中一个人的-1加到另一个人身上，自己的值指向另一个人的下标， 此时另一个人就作为这一个小团体的根，这之后如果有新的人进入这个团体，将新人的-1加到根上，再让新人指向根的下标。这样操作后，所有人中只要自己的值<0，则表明自己是一个团队的根，绝对值表示团队人数，而团体中的其他人均指向这个根。

2. 并查集的常见操作

我们通过上面的模拟，我们可以发现并查集的主要操作主要是：合并，查找根，查看团队个数

我们使用C++实现这个数据结构有

#pragma once
#include <vector>

using namespace std;

class UnionFindSet
{
public:
	// 将并查集中的所有元素初始化为-1
	UnionFindSet(size_t n)
		:_ufs(n, -1)
	{}

	// 查找根
	int FindRoot(int x);

	// 合并
	void Union(int x1, int x2);

	// 查看集合个数
	size_t UnionCount(int x);

private:
	vector<int> _ufs; 
};

1. 查找根

// 查找根
int FindRoot(int x)
{
	if (x >= _ufs.size())
	{
		throw invalid_argument("无效参数!");
		return -1;
	}

	int root = x;
	while (_ufs[root] >= 0) // 不为根就向上查找
	{
		root = _ufs[root];
	}

	return root;
}

2. 合并

在合并时，有可能会出现两个团队互相合并的情况，此时我们只需要将其中一个团队的根的值加到另一个团队的根上，再让自己指向另一个团队的根即可，即

// 合并
void Union(int x1, int x2)
{
	int root1 = FindRoot(x1);
	int root2 = FindRoot(x2);

	// 两个人属于不同的集合时，才需要进行合并
	if (root1 != root2)
	{
		_ufs[root1] += _ufs[root2];
		_ufs[root2] = root1;
	}
}

3. 查看集合个数

// 查看集合个数
size_t UnionCount()
{
	size_t ret = 0;
	for (auto& e : _ufs)
	{
		if (e < 0) ret++;
	}

	return ret;
}

3. 并查集的实际应用

1. 省份数量

题目链接：LCR 116. 省份数量 - 力扣（LeetCode）

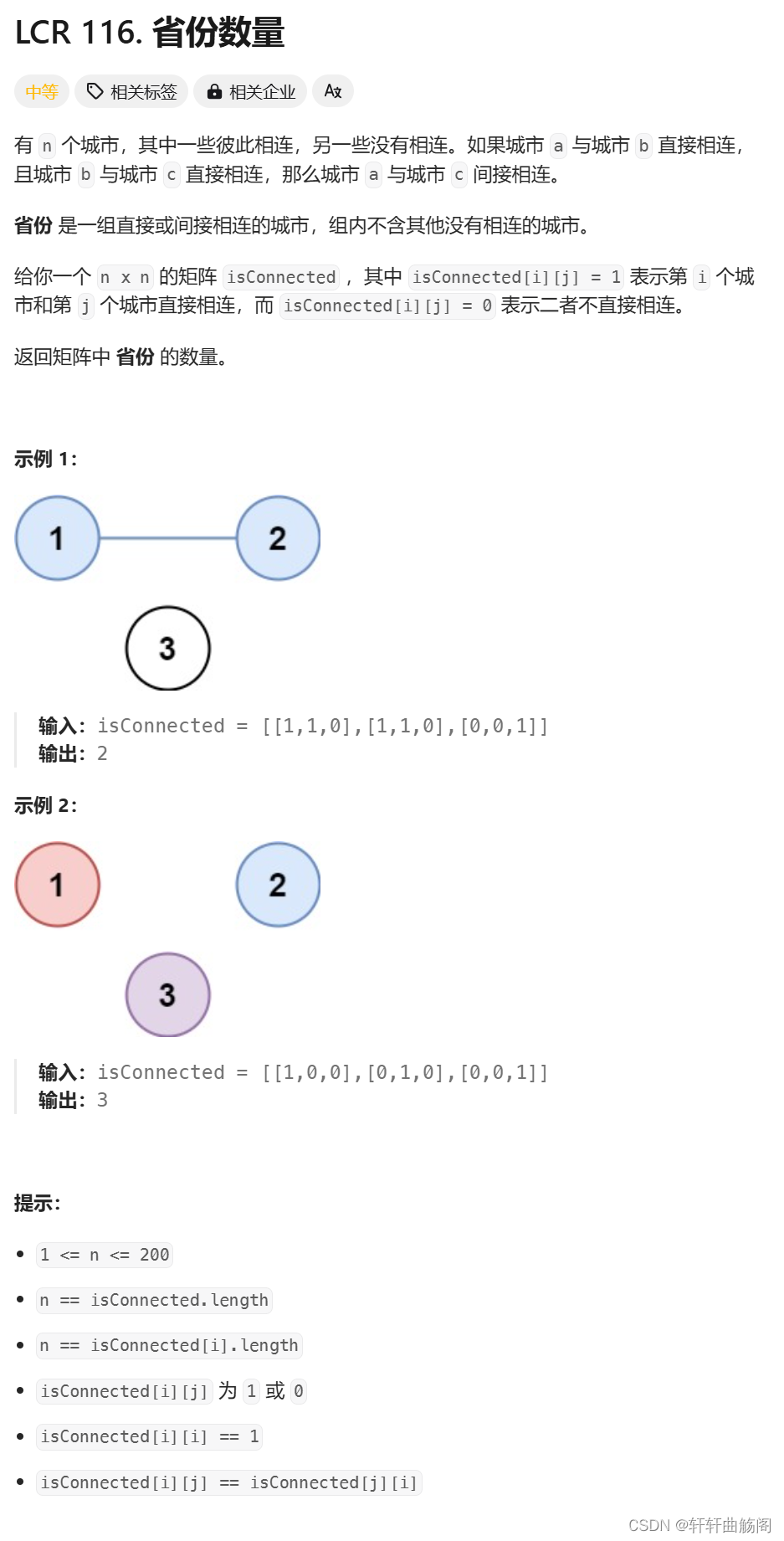
解析：分析题目，如果这道题使用并查集就没有那么难，整体思路就是如果两个城市相连就将他们合并为一个省份，最终返回省份个数即可

解法一：使用并查集数据结构
即

class UnionFindSet
{
public:
	// 将并查集中的所有元素初始化为-1
	UnionFindSet(size_t n)
		:_ufs(n, -1)
	{}

	// 查找根
	int FindRoot(int x)
	{
		if (x >= _ufs.size())
		{
			throw invalid_argument("无效参数!");
			return -1;
		}

		int root = x;
		while (_ufs[root] >= 0) // 不为根就向上查找
		{
			root = _ufs[root];
		}

		return root;
	}

	// 合并
	void Union(int x1, int x2)
	{
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);

		// 两个人属于不同的集合时，才需要进行合并
		if (root1 != root2)
		{
			_ufs[root1] += _ufs[root2];
			_ufs[root2] = root1;
		}
	}

	// 查看集合个数
	size_t UnionCount()
	{
		size_t ret = 0;
		for (auto& e : _ufs)
		{
			if (e < 0) ret++;
		}

		return ret;
	}

private:
	vector<int> _ufs;
};

class Solution
{
public:
	int findCircleNum(vector<vector<int>>& isConnected)
	{
		UnionFindSet ufs(isConnected.size());

		for (int i = 0; i < isConnected.size(); i++)
			for (int j = 0; j < isConnected[i].size(); j++)
				if (isConnected[i][j] == 1)
				{
					ufs.Union(i, j);
				}

		return ufs.UnionCount();
	}
};

 解法二：直接运用并查集思想

即

2. 等式方程的可满足性

题目链接：990. 等式方程的可满足性 - 力扣（LeetCode）