引言:
排序是计算机科学中最基础且重要的操作之一。本文将从排序的基本概念出发,详细讲解插入排序、选择排序、交换排序、归并排序和非比较排序的核心思想,并提供代码实现、复杂度分析及实际应用场景。通过对比不同算法的性能,帮助读者全面掌握排序算法的核心知识。
一、排序基础概念
1.1 什么是排序?
排序是将一组记录按照某个或某些关键字的大小,以递增或递减的顺序重新排列的过程。例如:
- 购物筛选:按价格从低到高排序商品。
- 院校排名:按总分从高到低排列高校。
1.2 排序算法的分类
- 比较排序:通过比较元素大小进行排序(如插入排序、快速排序)。
- 非比较排序:不直接比较元素大小(如计数排序)。
二、插入排序
2.1 直接插入排序
核心思想
将待排序元素依次插入已排序序列的合适位置,类似整理扑克牌。
当插入第 i(i>=1) 个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用 array[i] 的排序码与 array[i-1],array[i-2],… 的排序码顺序进行比较,找到插入位置即将 array[i] 插入,原来位置上的元素顺序后移
代码实现
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
int end = i;//已排好序的数组的最后一个元素
int tmp = a[end + 1];
// 将tmp插入到已排序序列的合适位置
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end]; // 元素后移
end--;//依次往前比较
}
else
{
break;
}
}
a[end + 1] = tmp; // 插入tmp
}
}
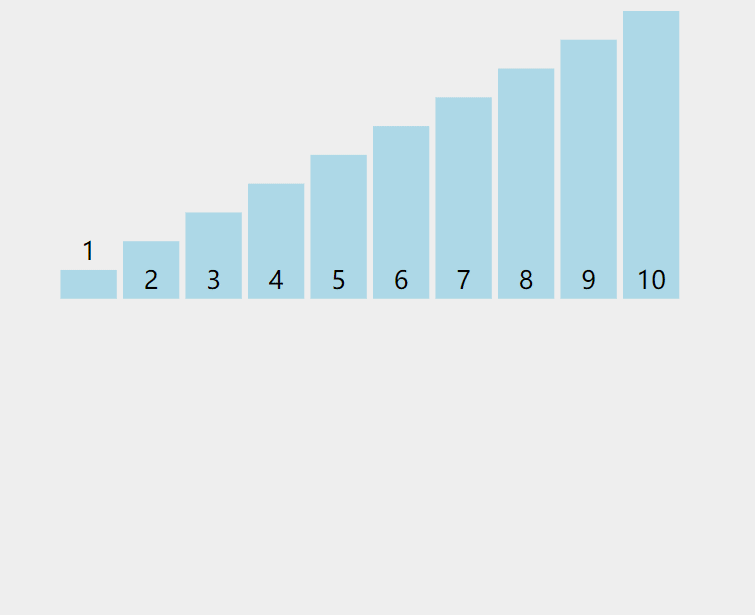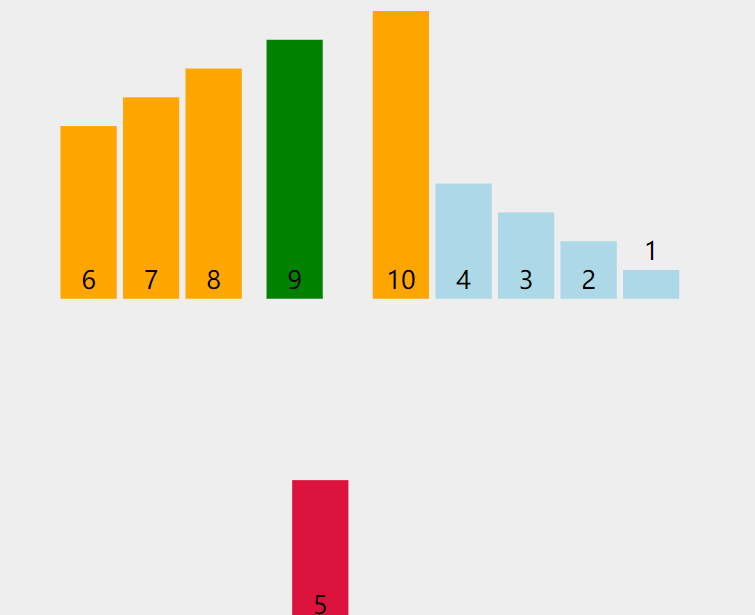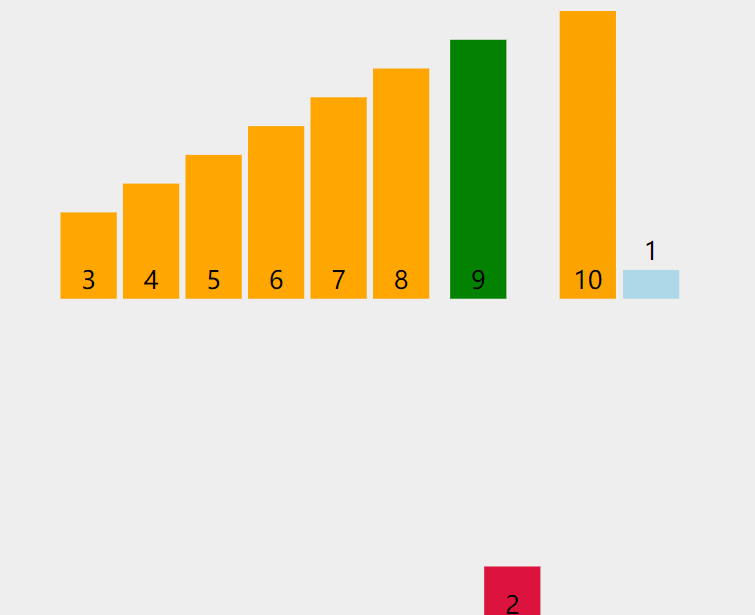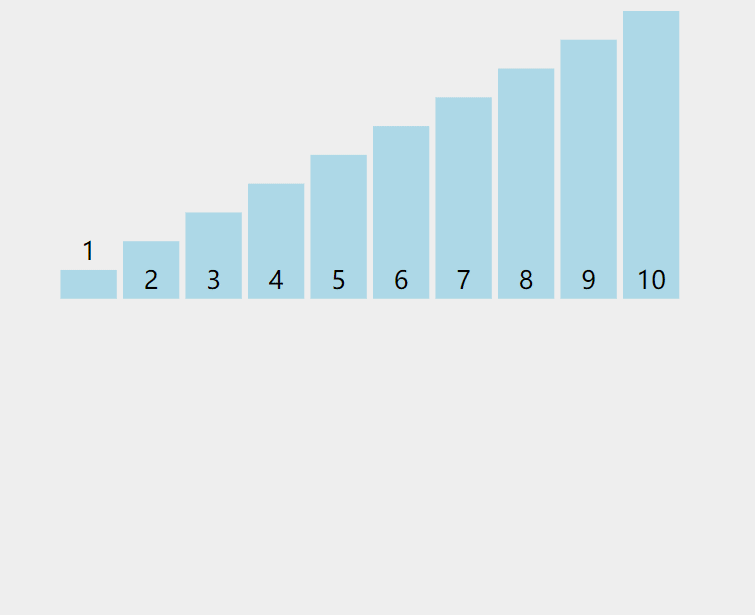
- 时间复杂度:平均和最坏情况为 O ( N 2 ) O(N^2) O(N2)(最坏:1+2+3+4…+n-1),最好情况(已有序)为 O ( N ) O(N) O(N)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
2.2 希尔排序(直接插⼊排序的优化)
核心思想
通过增量序列(如 gap = n/3 + 1)将数组分组,对每组进行插入排序,逐步缩小增量直至 gap=1。
代码实现
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//gap > 1 预排序,让数组更接近于有序
gap = gap / 3 + 1; // 动态调整增量,gap = 1 直接插入排序
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];//元素后移
end -= gap;//依次往前比较
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}

- 时间复杂度: O ( N 1.3 ) O(N^{1.3}) O(N1.3)(经验值),优于直接插入排序。
希尔排序的时间复杂度估算:
外层循环:
外层循环的时间复杂度可以直接给出为: O(log2 n) 或者 O(log3 n) ,即 O(log n)
内层循环:
假设⼀共有n个数据,合计gap组,则每组为n/gap个;在每组中,插⼊移动的次数最坏的情况下为,⼀共是gap组,因此: 1 + 2 + 3 + … + (n/gap− 1))
总计最坏情况下移动总数为: gap ∗ [1 + 2 + 3 + … + ( n/gap -1)]
gap取值有(以除3为例):n/3 n/9 n/27 … 2 1
• 当gap为n/3时,移动总数为: n/3 ∗ (1 + 2) = n
• 当gap为n/9时,移动总数为: n/9 * (1 + 2 + 3 + … + 8) = n/9 * 8(1 + 8) /2 = 4n
最后⼀躺,gap=1即直接插⼊排序,内层循环排序消耗为n
通过以上的分析,可以画出这样的曲线图:
因此,希尔排序在最初和最后的排序的次数都为n,即前⼀阶段排序次数是逐渐上升的状态,当到达某⼀顶点时,排序次数逐渐下降至n,而该顶点的计算暂时⽆法给出具体的计算过程.
不过经过专家们的估算差不多在N^1.3左右
- 空间复杂度: O ( 1 ) O(1) O(1)。
三、选择排序
3.1 直接选择排序
核心思想
每次从未排序序列中选择最小(或最大)元素,放到已排序序列的末尾。
代码实现
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;//同时找最大和最小
for (int i = begin; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
swap(&a[begin], &a[mini]); // 将最小值放到前面
if (maxi == begin)
{
//当begin刚好为最大值时
maxi = mini; // 防止最大值被覆盖
}
swap(&a[end], &a[maxi]); // 将最大值放到后面
begin++;
end--;
}
}
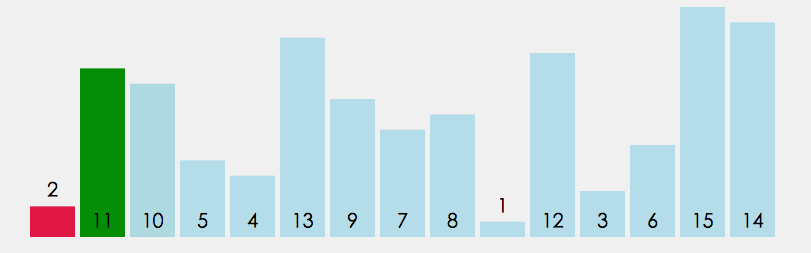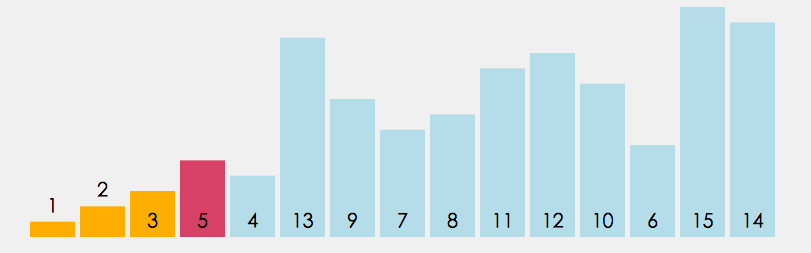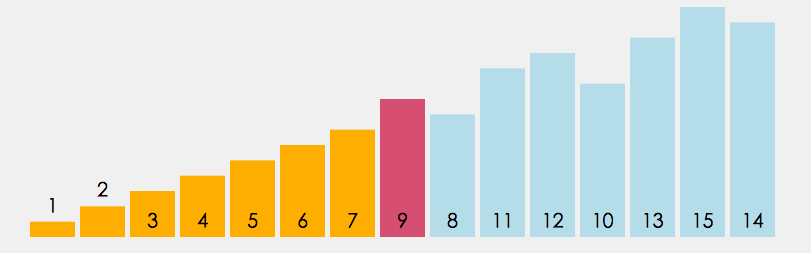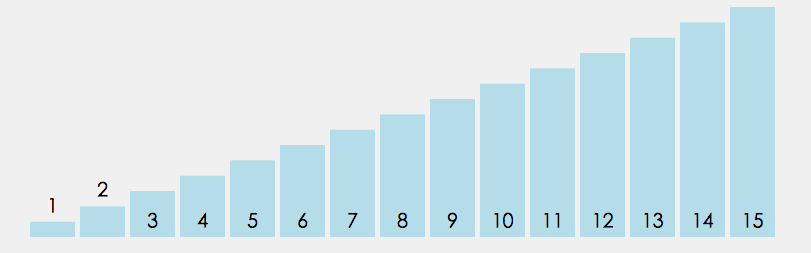
- 时间复杂度: O ( N 2 ) O(N^2) O(N2)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
3.2 堆排序(详见我的上一篇博客)
核心思想
通过构建大根堆(升序)或小根堆(降序),依次将堆顶元素与末尾元素交换并调整堆。
- 时间复杂度: O ( N log N ) O(N \log N) O(NlogN)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
四、交换排序
4.1 冒泡排序
核心思想
通过相邻元素的比较和交换(两两比较),将最大元素“冒泡”到末尾。
代码实现
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n; i++) //控制趟数 只需要n-1趟
{
int flag = 0; // 优化:若未发生交换则提前结束
for (int j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
{
swap(&a[j], &a[j + 1]);
flag = 1;
}
}
if (flag == 0)
{
break;
}
}
}
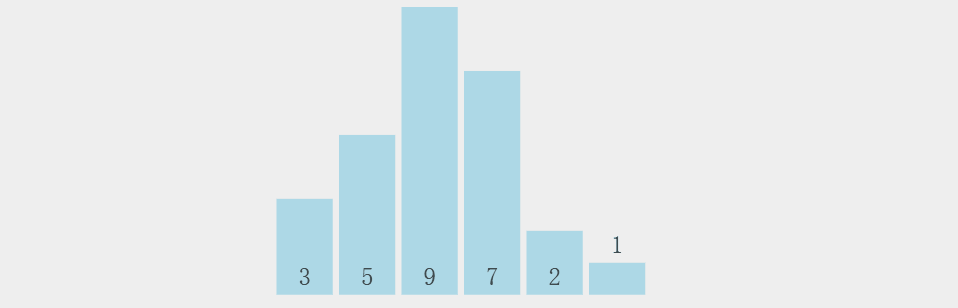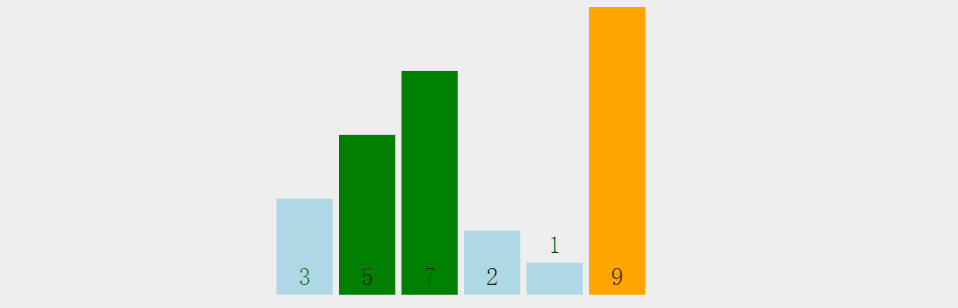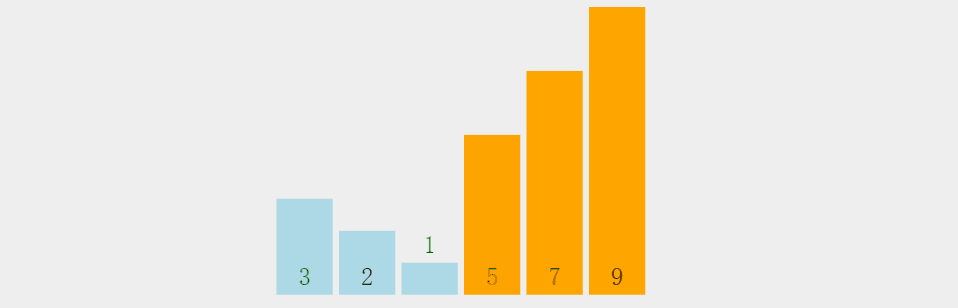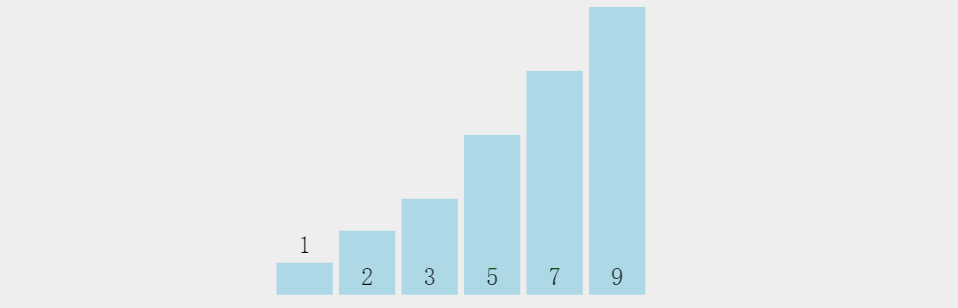
- 时间复杂度:平均和最坏情况为 O ( N 2 ) O(N^2) O(N2),最好情况为 O ( N ) O(N) O(N)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
4.2 快速排序
核心思想
分治法:选择一个基准值,将数组分为左右两部分(左小右大),递归处理子数组。
实现方式
1. Hoare版本
(1)创建左右指针left 和 right,确定基准值keyi
(2)right 从右向左找出比基准值小的数据,left 从左向右找出比基准值大的数据,左右指针数据交换,进入下次循环
(3)当left > right 时,keyi 和 right 交换(当 left > right 时,即right走到left的左侧而left扫描过的数据均不大于keyi,因此right此时指向的数据⼀定不大于keyi)
代码示例:
int _QuickSort(int* arr, int left, int right)
{
int keyi = left;
left++;//从第二个元素开始比较查找
//left <= right 交换
//left > right keyi 和 right 交换
while (left <= right)
{
//right:从右往左走,找比基准值小
while (left <= right && arr[right] > arr[keyi])
{
right--;
}
//left:从右往左走,找比基准值大
while (left <= right && arr[left] < arr[keyi])
{
left++;
}
//right找到比基准值小的,left找到比基准值大的
if (left <= right)
{
Swap(&arr[left++], &arr[right--]);
}
}
Swap(&arr[keyi], &arr[right]);//即使是right的值和keyi相等也交换
return right;
}
void QuickSort(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int keyi = _QuickSort1(arr, left, right);//找基准值
QuickSort1(arr, left, keyi - 1);//递归基准值左边区间
QuickSort1(arr, keyi + 1, right);//递归基准值右边区间
}

但是如果数组中存在大量重复的数据呢?这时候,不仅代码运行时间长,而且还会出现无效的排序

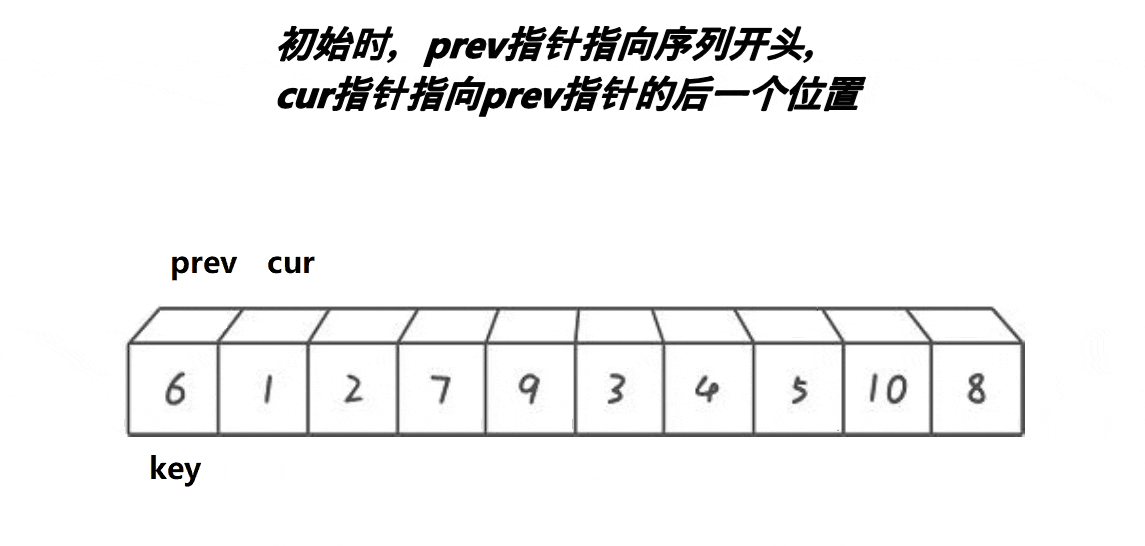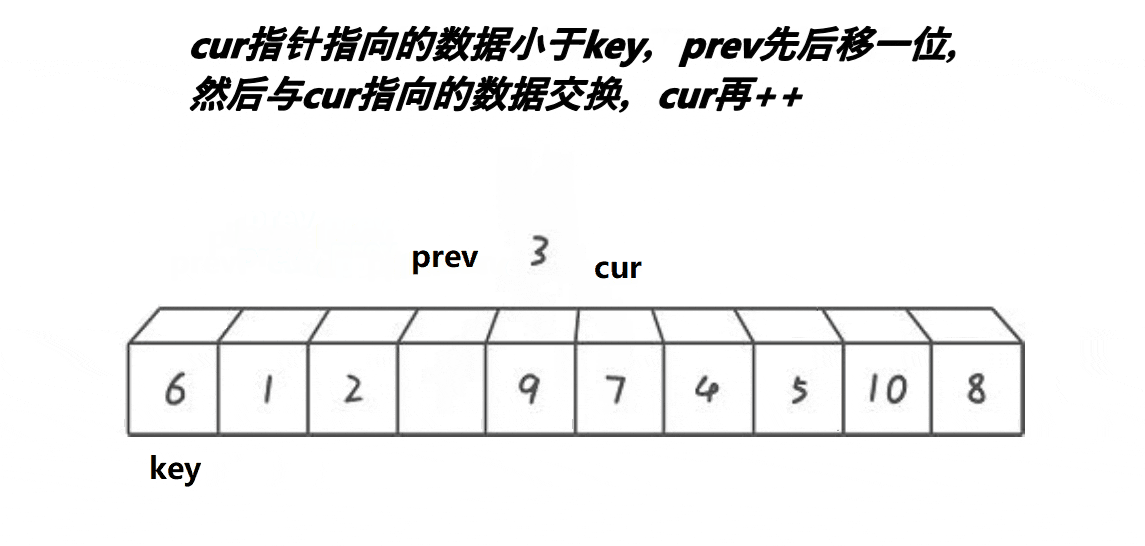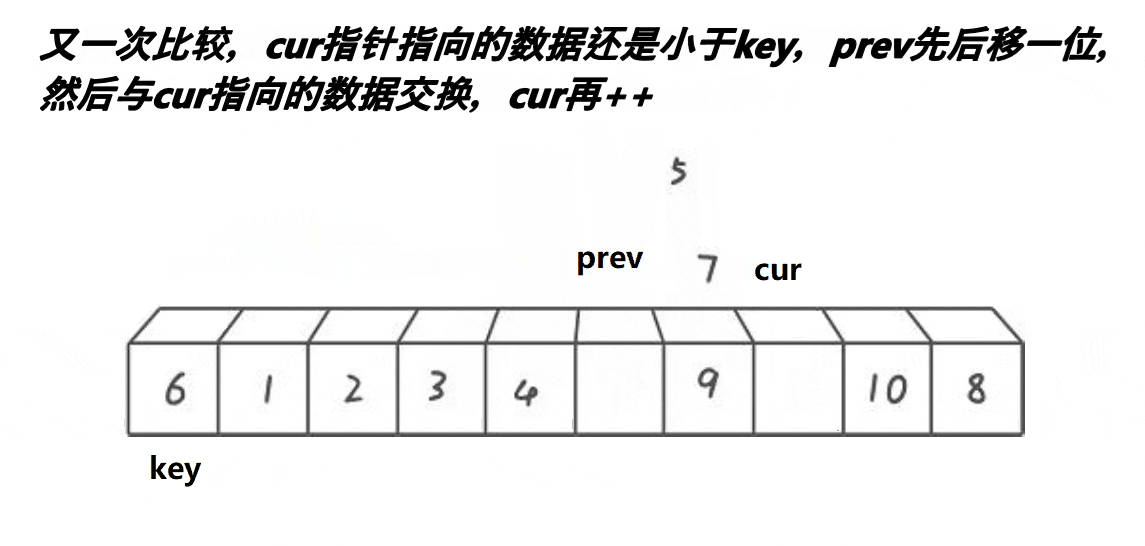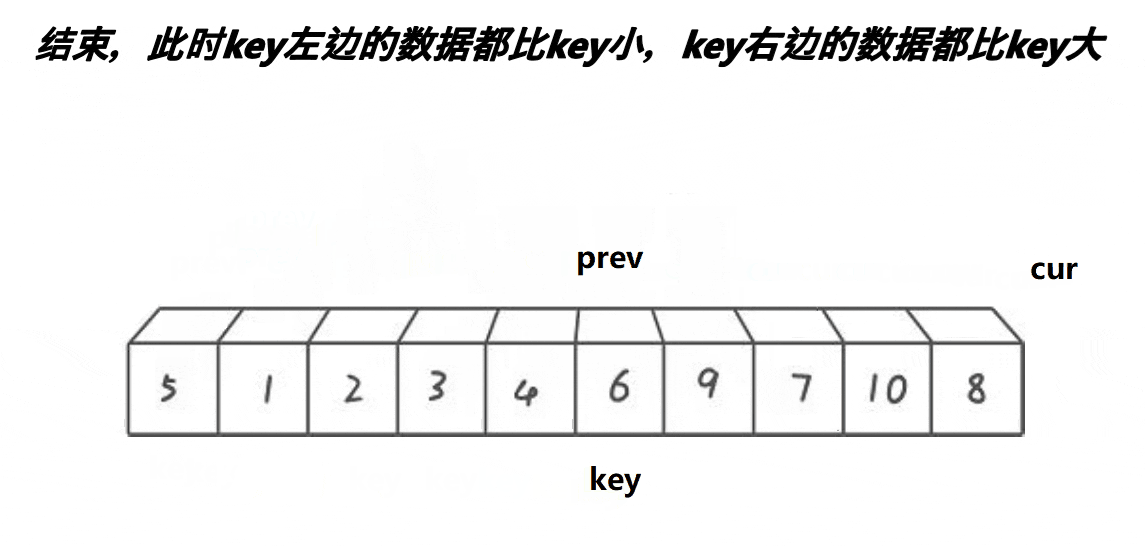
2. lomuto前后指针
prev 指针标记小于基准值的边界,cur 指针扫描数组。
代码示例:
//lomuto前后指针
int _QuickSort(int* arr, int left, int right)
{
int keyi = left;
int prev = left;
int cur = prev + 1;//cur找比基准值小的数据
while (cur <= right)
{
if (arr[cur] < arr[keyi] && ++prev != cur)
{
Swap(&arr[prev], &arr[cur]);
}
cur++;
}
Swap(&arr[keyi],&arr[prev]);
return prev;
}
void QuickSort(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
//找基准值
int keyi = _QuickSort(arr, left, right);
//left keyi right
//左序列[left,keyi-1] 右序列[keyi+1,right]
QuickSort(arr, left, keyi - 1);
QuickSort(arr, keyi + 1, right);
}
这个方法代码简单,但是思路不好想,而且也不能完全解决存在大量重复数据的情况。
3. 非递归实现—借助栈
void QuickSorkNor(int* arr, int left, int right)
{
ST st;
STInit(&st);
STPush(&st, left);
STPush(&st, right);
while (!STEmpty(&st))
{
//栈不为空,取栈顶
int end = STTop(&st);
STPop(&st);
int begin = STTop(&st);
STPop(&st);
//[begin,end]找基准值
int keyi = begin;
int prev = begin;
int cur = prev + 1;
while (cur <= end)
{
if (arr[cur] < arr[keyi] && ++prev != cur)
{
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[keyi], &arr[prev]);
keyi = prev;
//begin keyi end
//左序列 [begin,keyi-1] 右序列[keyi+1,end]
if (end > keyi + 1)
{
STPush(&st, keyi + 1);
STPush(&st, end);
}
if (begin < keyi - 1)
{
STPush(&st, begin);
STPush(&st, keyi - 1);
}
}
STDestroy(&st);
}
4. 三路划分 (处理大量重复数据的情况)
三路:小的放左边,大的放右边,相等放中间
算法思路:
1.keyi默认取left位置的值
2.left指向区间最左边,right指向区间最右边,cur指向left+1位置
3.cur遇到比keyi小的值后跟left位置交换,换到左边,left++,cur++
4.cur遇到比keyi大的值后跟right位置交换,换到右边,right–
5.直到cur > right结束
代码示例:
void QuickSort(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int begin = left, end = right;
int keyi = arr[left];
int cur = left + 1;
while (cur <= right)
{
if (arr[cur] < keyi)
{
Swap(&arr[cur], &arr[left]);
left++;
cur++;
}
else if (arr[cur] > keyi)
{
Swap(&arr[cur], &arr[right]);
right--;
}
else
{
cur++;
}
}
QuickSort(arr, begin, left - 1);
QuickSort(arr, right+1, end);
}
5. 内省排序 (进阶,可不学)
如果使用递归版的快速排序,递归深度过深时,也可能会导致效时间复杂度退化,于是就有人提出了这种算法,在深度过深时,使用其他排序算法,避免时间复杂度退化。该算法结合了快速排序、堆排序和插入排序的优点,确保在各种情况下均能高效运行
void IntroSort(int* arr, int left, int right, int depth, int defaultDepth)
{
if (left > right)
{
return;
}
if (right - left + 1 < 16)//当需要排序的数据总数小于16,就可以使用选择排序,这时这个排序的效率是最高的
{
InsertSort(arr + left, right - left + 1);
return;
}
if (depth > defaultDepth)//深度检测器。深度大于一定程度,调用堆排序
{
HeapSort(arr + left, right - left + 1);
return;
}
depth++;
int begin = left, end = right;
int randi = left + (rand() % (right - left + 1));
Swap(&arr[left], &arr[randi]);//随机数取key
int prev = left, cur = prev + 1;
int keyi = left;
while (cur <= right)
{
if (arr[cur] < arr[keyi] && ++prev != cur)
{
Swap(&arr[cur], &arr[prev]);
}
++cur;
}
Swap(&arr[prev], &arr[keyi]);
keyi = prev;//使用的是lomuto版本的快排
IntroSort(arr, begin, keyi - 1, depth, defaultDepth);
//depth是当前的深度,defaultDepth是最大允许递归深度。
IntroSort(arr, keyi + 1, end, depth, defaultDepth);
}
void IntroQuickSort(int* a, int left, int right)
{
int depth = 0;
int logn = 0;
int N = right - left + 1;
for (int i = 1; i < N; i *= 2)
{
logn++;//计算目标深度,log2(N) 的近似值
}
IntroSort(a, left, right, depth, logn * 2);
}
- 时间复杂度:平均 O ( N log N ) O(N \log N) O(NlogN),最坏 O ( N 2 ) O(N^2) O(N2)(如数组已有序)。
- 空间复杂度: O ( log N ) O(\log N) O(logN)(递归栈深度)。
五、归并排序
核心思想
分治法:将数组递归拆分为子数组,排序后合并。
代码实现
void _MergeSort(int* arr, int left, int right,int* tmp)
{
if (left >= right)
{
return;
}
int mid = (right - left) / 2 + left;//取中间值优化
//分解
//左序列:[left,mid] 右序列[mid+1,right]
_MergeSort(arr, left, mid, tmp);
_MergeSort(arr, mid+1, right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = begin1;//临时数组下标
//合并两个有序数组为⼀个数组
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] > arr[begin2])
{
tmp[index++] = arr[begin2++];
}
else
{
tmp[index++] = arr[begin1++];
}
}
//当其中一个数组遍历完,说明另一个数组中还有元素
// 循环遍历另一个数组
while (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
while(begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
for (int i = left; i <= right; i++)
{
arr[i] = tmp[i];
}
}
void MergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(arr, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}

文件归并排序和非递归归并排序(进阶)
1.文件归并排序
int compare(const void* a, const void* b)
{
return (*(int*)a - *(int*)b);
}
int ReadNDataSortToFile(FILE* fout, int n, const char* file1)
{
int* arr = (int*)malloc(sizeof(int) * n);//创建数组存放抽取出的数据
if (arr == NULL)
{
perror("malloc error!");
return 0;
}
int x = 0;//记录抽取出的数据
int j = 0;
for (int i = 0; i < n; i++)
{
if (fscanf(fout, "%d", &x) == EOF)//从文件中抽取的数据
break;//如果x == EOF,说明文件中所有的数均已被抽出,跳出循环
arr[j++] = x;//j的大小等于已经被抽取的数据
}
//数组arr是空的,说明这个文件是空的,已经没有数据了
if (arr == 0)
{
free(arr);//退出之前记得释放申请的空间
return 0;
}
qsort(a, j, sizeof(int), compare);//给抽出的数据排序
//打开文件,file1和file2用来存储抽取出的排序好的数据,mfile用来存储归并好的两个文件
/*
const char* file1 = "file1.txt";
const char* file2 = "file2.txt";
const char* mfile = "mfile.txt";
*/
FILE* fin = fopen(file1, "w");//创建一个fin文件,存放排序好的数据
if (fin == NULL)
{
free(a);
perror("fopen error!");
return 0;
}
for (int i = 0; i < j; i++)
{
fprintf(fin, "%d\n", a[i]);//将数据放进文件中
}
free(arr);
fclose(fin);
return j;//返回的是实际读取到的数据个数。没有数据就返回0。
}
void MergeSortFile(const char* file1, const char* file2, const char* mfile)
{
//创建好三个临时文件,用来存储排序好的数据
FILE* fout1 = fopen(file1, "r");
if (fout1 == NULL)
{
perror("fopen1 error!");
return 0;
}
FILE* fout2 = fopen(file2, "r");
if (fout2 == NULL)
{
perror("fopen2 error!");
return 0;
}
//往这个文件中写入
FILE* mfin = fopen(mfile, "w");
if (mfin == NULL)
{
perror("mfin error!");
return 0;
}
int x1 = 0, x2 = 0;
int ret1 = fscanf(fout1, "%d", &x1);//把fout1的第一个数据赋值给ret
int ret2 = fscanf(fout2, "%d", &x2);//把fout2的第一个数据赋值给ret
//将两个文件的数据进行比较,由小到大依次放进mfile文件中
while (ret1 != EOF && ret2 != EOF)
{
if (x1 < x2)
{
fprintf(mfin, "%d\n", x1);
ret1 = fscanf(fout1, "%d", &x1);//上一个数据放置完成。赋值下一个数据
}
else
{
fprintf(mfin, "%d\n", x2);
ret2 = fscanf(fout2, "%d", &x2);
}
}
//当其中一个文件遍历完,说明另一个文件中还有元素
// 循环遍历另一个文件
while (ret1 != EOF)
{
fprintf(mfin, "%d\n", x1);
ret1 = fscanf(fout1, "%d", &x1);
}
while (ret2 != EOF)
{
fprintf(mfin, "%d\n", x2);
ret2 = fscanf(fout2, "%d", &x2);
}
fclose(fout1);
fclose(fout2);
fclose(mfin);
}
//创建一个含有随机N个数据的文件
void CreateNData()
{
int n = 1000000;
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error!");
return 0;
}
for (int i = 0; i < n; i++)
{
int x = rand() + i;
fprintf(fin, "%d\n", x);
}
fclose(fin);
}
int main()
{
//CreateNData();
//创建三个文件,用来排序
const char* file1 = "file1.txt";
const char* file2 = "file2.txt";
const char* mfile = "mfile.txt";
//给待排序数组创建一个临时文件
FILE* fout = fopen("data.txt", "r");
if (fout == NULL)
{
perror("fout fopen error!");
return 0;
}
int m = 100000;
//这个是读取要排序的数据,从fout里读取,是读取到这个file1和file2这个文件中,
//每个文件读取m个数据
ReadNDataSortToFile(fout, m, file1);//fout已经打开了文件
ReadNDataSortToFile(fout, m, file2);
//data.txt的文件非常大,一次排序不了全部的数据,要多次排序
while (1)//循环多次排序
{
//把这个file1和file2中的数据在归并到这个mfile中
MergeSortFile(file1, file2, mfile);
//删除file1和file2
remove(file1);
remove(file2);
//将mfile重命名为file1
rename(mfile, file1);
int n = 0;
if ((n = ReadNDataSortToFile(fout, m, file2)) == 0)//n=0,说明文件中已经没有数据需要排序了
break;
}
return 0;
}

2.非递归
void MergeSortNor(int* arr, int* tmp, int n)
{
int gap = 1;
while (gap < n)
{
//根据gap分组,两两合并
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//奇数个元素情况
if (begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
int index = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] > arr[begin2])
{
tmp[index++] = arr[begin2++];
}
else
{
tmp[index++] = arr[begin1++];
}
}
while (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
while(begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
memcpy(arr+i,tmp+i,sizeof(int) * (end2 - i + 1));
}
gap *= 2;
}
}

- 时间复杂度: O ( N log N ) O(N \log N) O(NlogN)。
- 空间复杂度: O ( N ) O(N) O(N)。
六、非比较排序
6.1 计数排序
核心思想
统计每个元素的出现次数,按顺序填充到结果数组中。
代码实现
void CountSort(int* a, int n)
{
int min = a[0], max = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] < min)
min = a[i];
if (a[i] > max)
max = a[i];
}
int range = max - min + 1;
int* count = (int*)calloc(range, sizeof(int));
// 统计频率
for (int i = 0; i < n; i++)
count[a[i] - min]++;
// 填充结果
int idx = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
a[idx++] = i + min;
}
free(count);
}

- 时间复杂度: O ( N + range ) O(N + \text{range}) O(N+range)。
- 空间复杂度: O ( range ) O(\text{range}) O(range)。
- 适用场景:数据范围集中且为整数。
七、排序算法对比

稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
这里就不一一举例了,自己下去画图分析
八、总结
排序算法的选择需综合考虑数据规模、数据特征和应用场景。本文详细讲解了常见排序算法的原理、实现及优化方法,并通过代码示例和性能对比帮助读者深入理解。掌握这些知识后,可以灵活选择适合的算法解决实际问题。

