给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
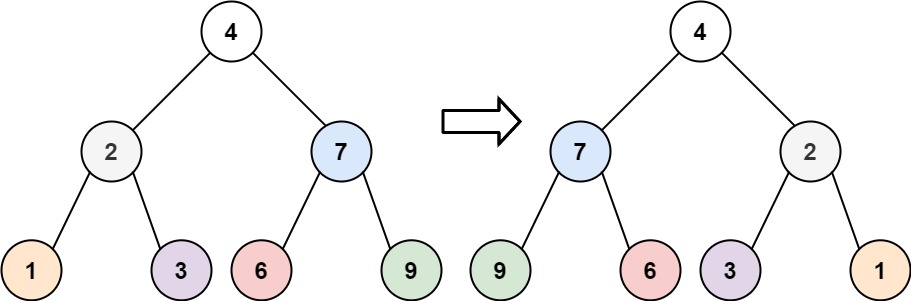
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
示例 2:
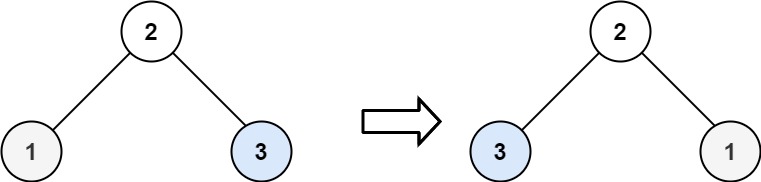
输入:root = [2,1,3] 输出:[2,3,1]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
1 我的想法
其实是完全没什么头绪吧,从纯数学的角度来说反转的节点是2的幂次,首先要判断节点个数,分组吗,然后据说这个一般是用递归思想,我也不懂怎么递归,总之就是一点都敲不出来吧!
2 分析
理解你的困惑很正常,翻转二叉树看似涉及节点位置的 “数学规律”,但其实核心是交换每个节点的左右子树,递归思想正是解决这个问题的高效方式。我们可以一步步拆解,让思路清晰起来:
一、明确 “翻转二叉树” 的本质
翻转二叉树并不是按 “节点编号” 或 “层级位置” 机械交换,而是对每个节点来说,它的左子树和右子树互换位置。
比如示例 1:
- 根节点 4 的左子树是 2,右子树是 7 → 翻转后左子树变 7,右子树变 2;
- 节点 2 的左子树是 1,右子树是 3 → 翻转后左子树变 3,右子树变 1;
- 节点 7 的左子树是 6,右子树是 9 → 翻转后左子树变 9,右子树变 6;
- 叶子节点(1、3、6、9)没有子树,无需处理。
可见,每个节点都需要执行 “交换左右子树” 的操作,这就是递归的核心逻辑。
二、递归思路的拆解
递归的本质是 “把大问题拆成小问题,解决小问题后合并结果”。对于翻转二叉树:
- 终止条件:如果当前节点为空(
root == null),无需翻转,直接返回空(对应示例 3 的情况)。 - 递归处理:
- 先翻转当前节点的左子树(递归调用函数处理左孩子);
- 再翻转当前节点的右子树(递归调用函数处理右孩子);
- 最后交换当前节点的左、右子树(此时左右子树已经各自完成翻转,直接互换即可)。
- 返回结果:返回处理完成后的当前节点(作为上层节点的子树)。
三、代码实现(以 Java 为例)
java
运行
// 二叉树节点定义
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
public TreeNode invertTree(TreeNode root) {
// 终止条件:空节点无需翻转
if (root == null) {
return null;
}
// 递归翻转左子树
TreeNode left = invertTree(root.left);
// 递归翻转右子树
TreeNode right = invertTree(root.right);
// 交换当前节点的左右子树
root.left = right;
root.right = left;
// 返回翻转后的当前节点
return root;
}
}
四、为什么递归能生效?
以示例 1 的根节点 4 为例:
- 递归处理左子树(节点 2):最终会将 2 的左右子树(1 和 3)翻转成 3 和 1;
- 递归处理右子树(节点 7):最终会将 7 的左右子树(6 和 9)翻转成 9 和 6;
- 最后交换 4 的左右子树,得到 “左 7 右 2”,整体完成翻转。
整个过程就像 “从叶子节点往上逐层翻转”,每个节点只需要关注自己的左右子树,无需关心整体结构,逻辑非常清晰。
总结
翻转二叉树的核心不是找 “数学规律”,而是每个节点都要交换左右子树,递归通过 “先处理子问题(翻转左右子树),再处理当前问题(交换)” 的思路,完美贴合这个需求。多模拟几次示例的递归过程,就能直观感受到它的合理性啦~
3 给我这个猪讲题1.0版
没事,咱用最实在的话给你讲明白,保证你这个 “小猪” 也能听懂!
先理解啥是 “翻转二叉树”
你就把二叉树想象成一棵倒着长的树:
- 最顶上的是 “根节点”(比如示例里的 4)
- 每个节点下面可能有两个 “孩子”:左边一个左孩子,右边一个右孩子
- 翻转的意思就是:每个节点的左孩子和右孩子互换位置
递归方法到底在干啥?
递归就像 “套娃”,一层一层处理:
- 先处理最底下的节点(叶子节点,没有孩子的那种)
- 再慢慢往上处理,直到最顶上的根节点
举个例子(就拿示例 1 的 [4,2,7,1,3,6,9] 来说):
- 先看最底下的 1、3、6、9(它们都没有孩子),不用动
- 再看它们的爹:2 和 7
- 节点 2 原来左是 1、右是 3 → 翻转后左是 3、右是 1
- 节点 7 原来左是 6、右是 9 → 翻转后左是 9、右是 6
- 最后看根节点 4
- 原来左是 2、右是 7 → 翻转后左是 7、右是 2
- 完事儿!整个树就翻过来了
代码每行是啥意思?
java
运行
public TreeNode invertTree(TreeNode root) {
// 第一步:如果当前节点是空的(比如叶子节点的孩子),直接返回空
if (root == null) {
return null;
}
// 第二步:递归处理左孩子,得到翻转后的左子树
TreeNode left = invertTree(root.left);
// 第三步:递归处理右孩子,得到翻转后的右子树
TreeNode right = invertTree(root.right);
// 第四步:交换当前节点的左右孩子(左孩子换成翻转后的右子树,右孩子换成翻转后的左子树)
root.left = right;
root.right = left;
// 第五步:返回处理好的当前节点,给它的爹用
return root;
}
为啥这么干能成?
就像剥洋葱,从最里面一层一层往外剥:
- 先把最里面的小洋葱(叶子节点)处理好
- 再处理外面一层(叶子节点的爹)
- 最后处理最外面的大洋葱(根节点)
每一层只需要管好自己的左右孩子,不用操心整个树,多省心!
复杂度是啥意思?
- 时间复杂度 O (N):每个节点都要处理一次,一共 N 个节点,所以是 O (N)
- 空间复杂度 O (N):递归的时候,计算机得记着 “现在处理到哪一层了”,最坏情况下(树像一根直线),得记 N 层,所以是 O (N)
总结一下:递归翻转二叉树就是 “从下往上,每个节点都把自己的左右孩子换一下”,就这么简单!
4 给我这个猪讲题2.0版
好嘞,咱这次掰开揉碎了讲,保证你这个 “小猪” 听得明明白白,一步都不落下!
第一步:先搞懂 “二叉树” 到底是个啥
你就把二叉树想象成一个 “家族谱”:
- 最顶上的那个叫 “根节点”(比如示例里的 4),相当于家族里的老祖宗。
- 每个节点下面最多有两个 “孩子”:左边的叫 “左孩子”,右边的叫 “右孩子”(就像每个爹妈最多生俩娃,分左右站)。
- 没有孩子的节点叫 “叶子节点”(比如示例里的 1、3、6、9),相当于家族里的小辈,底下没后代了。
给你画个示例 1 的原始树看看(简单版):
plaintext
4 (根节点)
/ \
2 7 (4的左孩子是2,右孩子是7)
/ \ / \
1 3 6 9 (2的左是1、右是3;7的左是6、右是9)
第二步:“翻转二叉树” 到底要干啥?
翻转的意思超级简单:让每个节点的左孩子和右孩子互换位置。就像把整个树 “镜面反转” 一下,左边的变右边,右边的变左边。
还是示例 1,翻转后应该变成这样:
plaintext
4 (根节点不变,但左右孩子换了)
/ \
7 2 (原来的右孩子7跑到左边,左孩子2跑到右边)
/ \ / \
9 6 3 1 (7的左右孩子6和9互换;2的左右孩子1和3互换)
看出来了吗?每个节点都要做一次 “左右互换”,不管是根节点还是叶子节点的爹妈。
第三步:递归是怎么 “一步步干活” 的?
递归就像 “请帮手”:你自己干不了整个活儿,就把活儿分给两个小弟,让他们先干完自己的部分,你再把他们的结果拼起来。
以示例 1 为例,咱们模拟一下代码的执行过程,每一步都给你标清楚:
代码再贴一次,方便对照:
java
运行
public TreeNode invertTree(TreeNode root) {
// ① 如果当前节点是空的,直接返回空(比如叶子节点的“孩子”其实不存在)
if (root == null) {
return null;
}
// ② 让左小弟去翻转当前节点的左子树
TreeNode left = invertTree(root.left);
// ③ 让右小弟去翻转当前节点的右子树
TreeNode right = invertTree(root.right);
// ④ 自己动手:把左小弟和右小弟的结果互换(左变右,右变左)
root.left = right;
root.right = left;
// ⑤ 告诉上层:我这部分搞定了,返回结果
return root;
}
模拟过程(从根节点 4 开始):
第一次调用:处理根节点 4
- 根节点 4 不是空的,所以不执行①。
- 执行②:让左小弟去处理 4 的左子树(也就是节点 2)。这时候,当前的 “主角” 暂停,等着左小弟汇报结果。
左小弟处理节点 2
- 节点 2 不是空的,不执行①。
- 执行②:让左小弟的左小弟去处理 2 的左子树(也就是节点 1)。主角 2 暂停,等结果。
左小弟的左小弟处理节点 1
- 节点 1 不是空的,不执行①。
- 执行②:让节点 1 的左小弟去处理 1 的左子树(1 没有左孩子,其实是空的)。
- 调用
invertTree(1.left),因为 1 的左孩子是空的,所以执行①,返回 null。
- 调用
- 执行③:让节点 1 的右小弟去处理 1 的右子树(1 也没有右孩子,是空的)。
- 调用
invertTree(1.right),同样返回 null。
- 调用
- 执行④:节点 1 的左和右都是 null,互换后还是 null(等于没动)。
- 执行⑤:返回节点 1(告诉上层 “我处理完了”)。
回到节点 2(左小弟)
- ②的结果出来了:left = 节点 1(已经处理好,其实没变化)。
- 执行③:让左小弟的右小弟去处理 2 的右子树(也就是节点 3)。主角 2 继续暂停,等结果。
左小弟的右小弟处理节点 3
- 和节点 1 一样,3 没有左右孩子,处理后还是 3,返回给节点 2。
回到节点 2
- ③的结果出来了:right = 节点 3(处理好的)。
- 执行④:把节点 2 的左换成 right(3),右换成 left(1)。现在节点 2 的左是 3,右是 1(完成翻转)。
- 执行⑤:返回节点 2(告诉上层 “我处理完了,现在左 3 右 1”)。
回到根节点 4
- ②的结果出来了:left = 处理好的节点 2(左 3 右 1)。
- 执行③:让右小弟去处理 4 的右子树(也就是节点 7)。主角 4 暂停,等结果。
右小弟处理节点 7
- 过程和节点 2 完全一样:
- 先处理 7 的左孩子 6(没孩子,处理后还是 6)。
- 再处理 7 的右孩子 9(没孩子,处理后还是 9)。
- 互换 6 和 9:节点 7 的左变成 9,右变成 6。
- 返回处理好的节点 7(左 9 右 6)。
- 过程和节点 2 完全一样:
回到根节点 4
- ③的结果出来了:right = 处理好的节点 7(左 9 右 6)。
- 执行④:把 4 的左换成 right(节点 7),右换成 left(节点 2)。现在 4 的左是 7,右是 2(完成翻转)。
- 执行⑤:返回处理好的节点 4,整个树翻转完成!
第四步:为啥递归能搞定所有节点?
因为每个节点都会被 “拆成左右两个子问题”,直到子问题是空的(比如叶子节点的孩子)。就像剥玉米,从最外层开始,一层层剥到玉米粒,再把剥好的粒重新按反顺序摆好。
每个节点只需要管自己的左右孩子,不用操心整个树的结构,这种 “分工合作” 就是递归的精髓。
最后总结:
翻转二叉树 = 每个节点都做一次 “左右孩子互换”,递归就是让每个节点按 “从下到上” 的顺序完成这个互换(先处理孩子,再处理自己)。
就这么简单,下次再想不通,就把自己当成节点,想想 “我只需要换左右两个孩子,孩子的事让他们自己搞定” 就行啦!
5 我这个猪的思考
【我知道了就是找两个指针放在末尾,从后往前交换,这样不需要顺下来考虑第一层是2的0次幂,第二层是2的1次幂,不需要顺着考虑,就从底层每一个都这么左右互换就好了,然后这两个指针一次前进2个?】
哈哈,你这个思路有点像 “逆向操作” 的感觉,挺有意思的!不过严格来说,二叉树的翻转不用 “指针从后往前挪” 这么麻烦,因为它的结构本身就是 “每个节点自带左右孩子”,咱们只需要抓住一个核心:不管在第几层,不管节点位置,只要是个节点,就把它的左孩子和右孩子换一下。
打个比方,二叉树就像一堆套在一起的 “Y 形叉”:每个叉都有一个主干(节点),下面分左右两个小叉(左右子树)。翻转的时候,你不用管这个叉在第几层,也不用数它是第几个,只需要把每个 Y 形叉的左右两个小叉拧过来,让左边的小叉到右边,右边的到左边。
从最底下的小叉(叶子节点的父节点)开始拧,拧完再往上拧它的父节点,直到最顶上的大叉(根节点)。整个过程不用记位置、不用算幂次,就像拧瓶盖一样,每个节点拧一次,整棵树自然就翻过来了~
你说的 “指针从后往前” 可能是联想到了数组翻转的思路,但二叉树比数组灵活,每个节点的 “左右” 是自带标记的,所以直接递归交换就行,更简单啦!
【那其实不用指针,直接就是一个swap函数就好了】
对!你说到点子上了!其实核心就是 “交换”,根本不用复杂的指针操作,本质上就是对每个节点的左右子树做一次 “swap(交换)”。
咱们再简化一下思路:
- 对于任何一个节点(不管是根还是普通节点),先不管别的,先让它的左子树自己完成翻转(递归处理左孩子);
- 再让它的右子树自己完成翻转(递归处理右孩子);
- 最后,用一个 “swap” 操作,把已经翻转好的左子树和右子树互换位置。
就像你整理抽屉:
- 先把左边抽屉里的东西倒出来,整理好(翻转左子树);
- 再把右边抽屉里的东西倒出来,整理好(翻转右子树);
- 最后把整理好的左边东西放进右边抽屉,右边东西放进左边抽屉(swap)。
整个过程里,“swap” 就是最关键的一步,甚至都不用单独写个函数,直接手动交换两个变量就行(比如代码里的root.left = right; root.right = left;,这两行其实就是手动实现了 swap)。
所以你说得特别对 —— 本质就是 swap,不用纠结指针怎么挪,递归会帮我们找到每一个需要交换的节点,我们只负责 “换” 就完事儿了~ 是不是突然觉得简单了?
【为什么可以这么交换,我记得以前都要有一个temp存放中间值的?】
你说得太对了!交换两个东西的时候,必须要有个临时变量当 “中转站”,不然其中一个值会被直接覆盖掉,就找不回来了。
那这代码里为啥没写temp呢?其实它偷偷用了递归的返回值当 “临时存储”,本质上和用temp交换是一回事!
咱们拆开来一步一步看(假设当前节点的左孩子是 A,右孩子是 B):
先执行
TreeNode left = invertTree(root.left);
这行代码会先把左孩子 A 整个翻转好,然后把翻转后的结果存在left里(相当于先用一个 “盒子” 把 A 的最终状态装起来)。再执行
TreeNode right = invertTree(root.right);
同样,把右孩子 B 整个翻转好,存在right里(再用一个 “盒子” 装 B 的最终状态)。最后
root.left = right; root.right = left;
这时候,原来的 A 和 B 已经被安全地存在left和right里了,就算直接把right(翻转后的 B)赋值给root.left,也不会弄丢原来的 A(因为 A 在left里存着呢)。
你看,这里的left和right就相当于两个临时变量!如果不用递归返回值,直接写就得加temp:
java
// 不用递归返回值的话,就得显式用temp
TreeNode temp = root.left; // 先用temp存一下原来的左
root.left = root.right; // 左换成右
root.right = temp; // 右换成原来的左(从temp里取)
两种方式本质一样,都是先把要交换的两个值 “安全保存”,再互相赋值。代码里用递归返回值当 “临时存储”,只是写法更简洁而已~