目录
1.程序功能描述
生产调度是制造系统的核心环节,其目标是在满足资源约束(如设备产能、工序优先级)的前提下,优化多个相互冲突的目标(如最小化生产周期、成本、能耗等)。传统单一优化算法(如粒子群优化PSO、遗传算法GA)在多目标生产调度中存在收敛速度慢、解的多样性不足等问题。PSO-NSGAIII混合优化算法结合了粒子群优化(PSO)的高效局部搜索能力与第三代非支配排序遗传算法(NSGAIII)的多目标Pareto最优解搜索能力,能有效平衡解的收敛性与多样性,适用于复杂多目标生产调度问题。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行
以下三个图分别是NSGAIII,PSO,PSO-NSGAIII三组算法的甘特图:
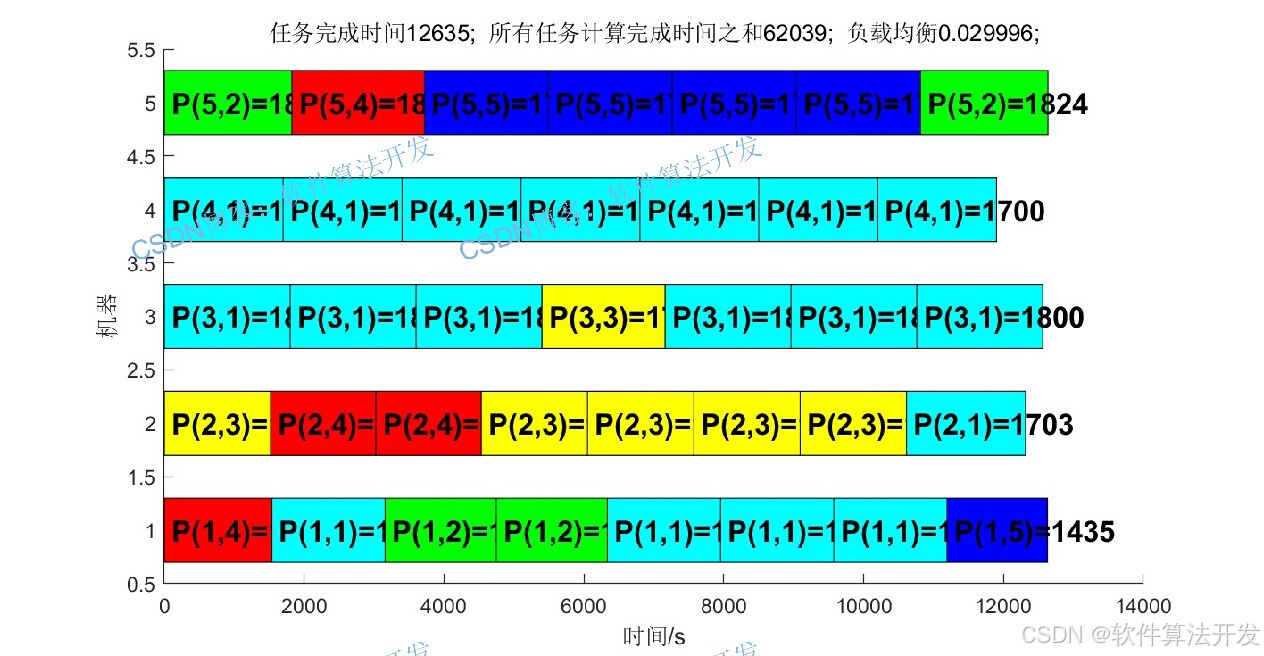
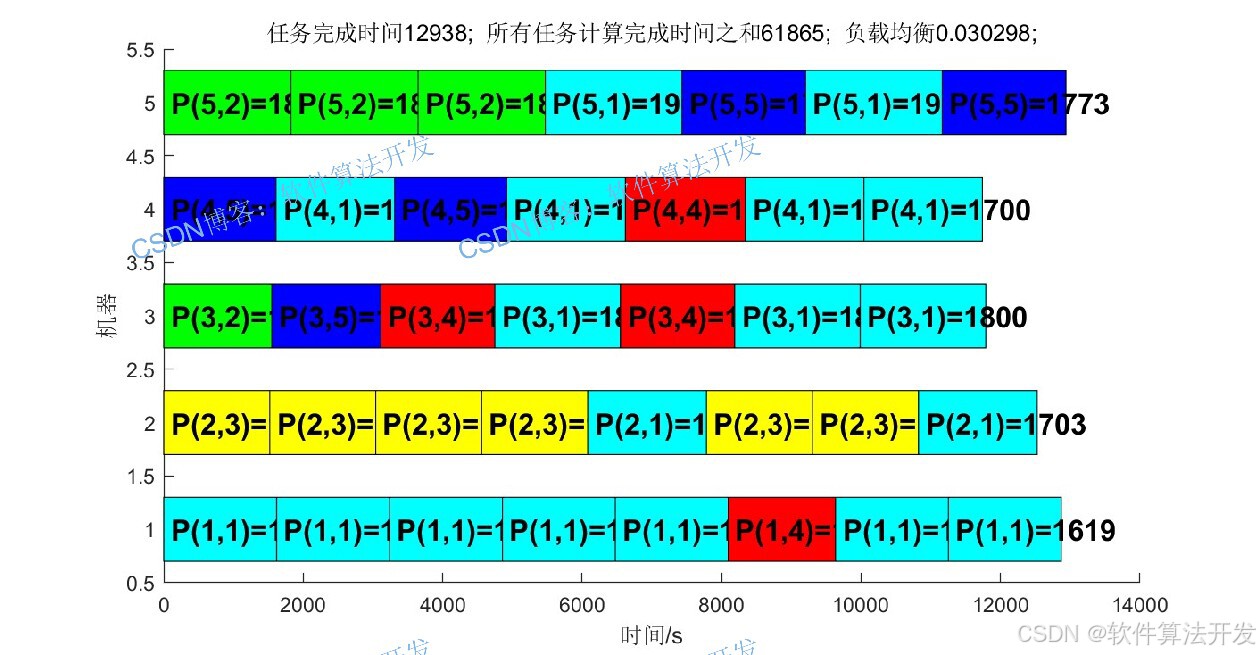
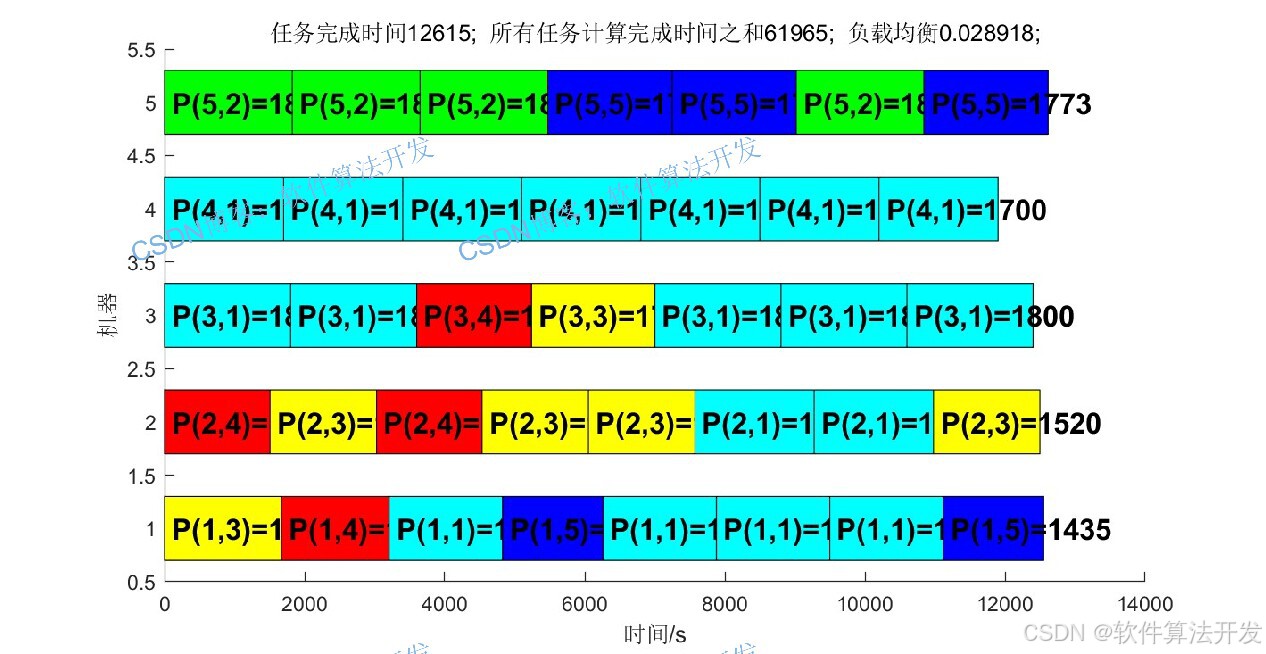
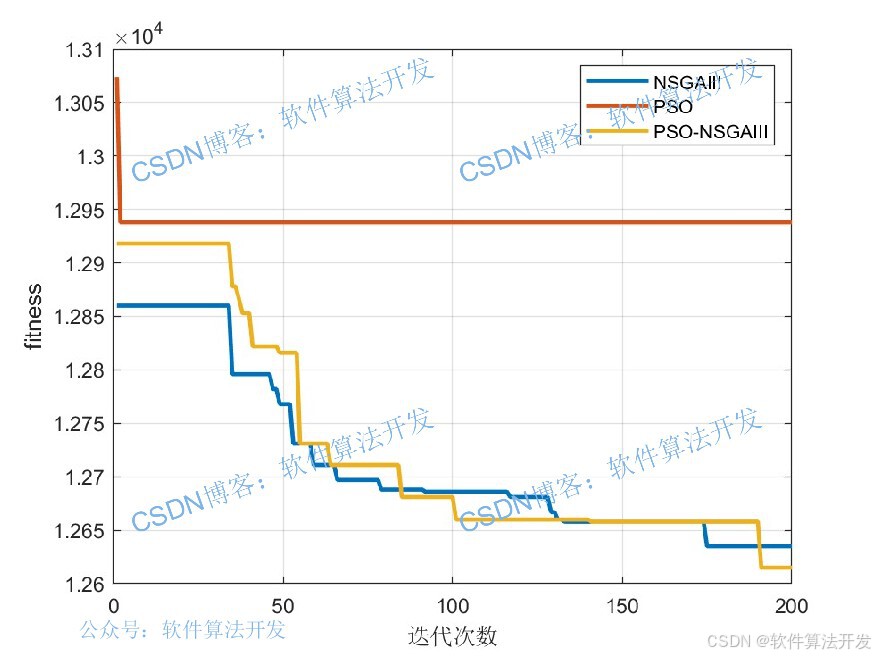
3.部分程序
N = 500; % 种群个数
M = 3; % 目标个数
gen = 200; %迭代次数
%Generate the reference points and random population
[Z,N] = UniformPoint(N,M); % 生成一致性参考解
[res,Population] = funfun(); % 生成初始种群与目标值
[RR,CC]=size(Population);
Pop_initial = Pop_initial/max(Pop_initial);
Population = Population+repmat(Pop_initial,[RR,1]);
Pop_objs = CalObj(Population); % 计算适应度函数值
Zmin = min(Pop_objs(all(PopCon<=0,2),:),[],1);
%Optimization
for i = 1:gen
i
ttt=i;
MatingPool = TournamentSelection(2,N,sum(max(0,PopCon),2));
Offspring = GA(Population(MatingPool,:));
Offspring_objs = CalObj(Offspring);
Zmin = min([Zmin;Offspring_objs],[],1);
Population = EnvironmentalSelection([Population;Offspring],N,Z,Zmin);
Popobj = CalObj(Population);
Y1 = Popobj(:,1);
Y2 = Popobj(:,2);
Y3 = Popobj(:,3);
tmps = Population;
zz(i) = min(10000*Y1);
end
06_102m4.算法理论概述
PSO-NSGAIII混合算法的本质是通过融合PSO的群体智能搜索机制与NSGAIII的多目标排序框架,构建 “全局探索 - 局部求精 - 多目标平衡” 的优化流程。其核心原理体现在三个方面:
生产调度问题的多目标性是算法设计的前提。以典型的作业车间调度问题(Job Shop Scheduling Problem, JSP)为例,其数学模型定义如下:

PSO的优势:通过粒子位置和速度的迭代更新实现群体搜索,收敛速度快,适合局部最优解的求精。其核心是粒子通过跟踪个体最优(pbest)和全局最优(gbest)更新自身状态。
NSGAIII的优势:通过非支配排序和参考点机制处理多目标优化,能有效保持 Pareto 最优解的多样性,避免陷入局部最优。
混合逻辑:
用NSGAIII的非支配排序和参考点选择策略构建全局最优解集合(精英库),替代PSO中的单一 gbest;
用PSO的速度-位置更新公式实现粒子的局部搜索,增强算法对解空间的探索能力;
结合NSGAIII的选择、交叉操作与PSO的变异机制,平衡种群的多样性与收敛性。
PSO-NSGAIII混合算法的实现分为7个核心步骤:
步骤 1:种群初始化
种群由N个粒子组成,每个粒子代表一个可行的生产调度方案(即决策变量π的一个实例)。
步骤 2:适应度评估
对每个粒子(调度方案)计算其多目标函数值,并评估可行性。
步骤 3:非支配排序(NSGAIII 核心步骤)
对种群中的所有粒子进行非支配排序,划分Pareto等级,筛选精英解。
步骤 4:参考点关联与种群多样性保持(NSGAIII核心步骤)
通过参考点机制确保Pareto最优解的均匀分布,为PSO提供多样化的全局最优候选。
步骤 5:粒子更新(PSO核心步骤)
基于NSGAIII筛选的精英解,通过PSO的速度 - 位置公式更新粒子,实现局部求精。
步骤 6:交叉与变异(增强多样性)
结合NSGAIII的遗传操作与PSO的变异机制,避免种群早熟。
步骤 7:精英保留与迭代终止
精英保留:将父代种群与子代种群(经粒子更新、交叉变异生成)合并,通过NSGAIII的非支配排序和参考点选择,保留前N个最优解作为下一代种群。
5.参考文献
[1]徐宜刚,陈勇,王宸,等.改进NSGA-III求解高维多目标绿色柔性作业车间调度问题[J].系统仿真学报, 2024(10).DOI:10.16182/j.issn1004731x.joss.23-0694.
[2]李长云 肖鸿洲 王志兵 李霆誉.基于改进的NSGA-III算法求解绿色柔性作业车间调度问题[J].企业科技与发展, 2024(12).
6.完整程序
VVV