数据结构初阶（9）二叉树链式结构的实现-EW帮帮网

4. 二叉树链式结构的实现

4.1 前置说明

x.0 头文件声明

#pragma once
#define _CRT_SECURE_NO_WARNINGS

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

#include"BT_Queue.h"

//二叉树的链式结构
typedef struct BinTreeNode
{
	struct BinTreeNode* left;
	struct BinTreeNode* right;
	int val;
}BTNode;

//二叉树相关的函数，使用递归算法，都是不断细分·左右子树去递归

//二叉树的遍历——
//前序
void PreOrder(BTNode* root);
//中序
void InOrder(BTNode* root);
//后序
void PostOrder(BTNode* root);

//求树中节点个数
int TreeSize(BTNode* root);
//找叶子节点数
int LeafNode(BTNode* root);    //传入根节点
//求树的高度
int maxDepth(BTNode* root);

//求树中第k层节点个数
int TreeKLevel(BTNode* root, int k);
//求x所在节点
BTNode* TreeFind(BTNode* root, int x);

//二叉树的销毁
void TreeDestroy(BTNode* root);

//二叉树的层序遍历
void TreeLevelOrder(BTNode* root);

//判断完全二叉树
bool TreeIsComplete(BTNode* root);

x.1 手搓一棵树

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。

由于现在对二叉树结构掌握还不够深入，为了降低学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习。

等二叉树结构了解的差不多时，再反过头再来研究二叉树真正的创建方式。

//Test.c

//创建一个树结点
BTNode* BuyBTNode(int val)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	newnode->val = val;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}

// 手搓一棵树
BTNode* CreateTree()
{
	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);
	BTNode* n4 = BuyBTNode(4);
	BTNode* n5 = BuyBTNode(5);
	BTNode* n6 = BuyBTNode(6);

	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n4->left = n5;
	n4->right = n6;

	return n1;
}

注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。

在看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：

1. 空树

2. 非空：根节点，根节点的左子树、根节点的右子树组成的。

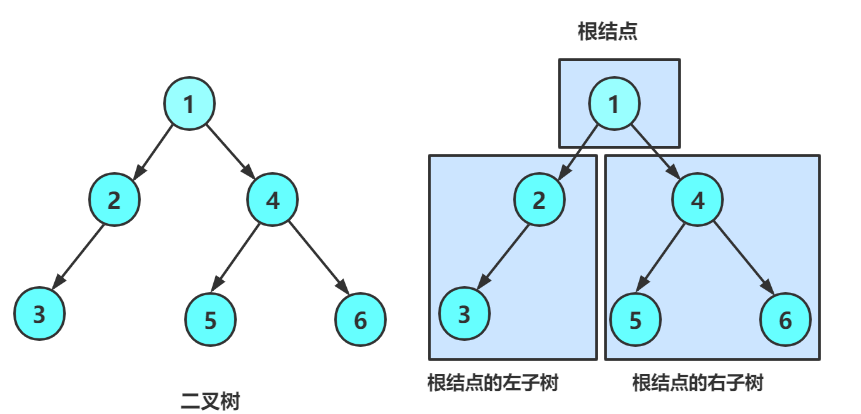
从概念中可以看出，二叉树的定义是递归式的：

二叉树分为：根、左子树、右子树。其中：

左子树分为：根、左子树、右子树。其中：

……

直到树为NULL为止。

因此后续基本操作中基本都是按照二叉树的递归概念实现的。

入门级递归：二叉树的遍历。

普通级递归：二叉树的其他接口。

中等级递归：二叉树的OJ题。

4.2 二叉树的遍历

4.2.1 前序、中序以及后序遍历

学习二叉树结构，最简单的方式就是遍历。

之前学的数据结构比较简单，只有一种遍历方式，二叉树比较复杂，有多种遍历方式

二叉树遍历(Traversal)：是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。

访问结点所做的操作依赖于具体的应用问题。

遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

根据二叉树，建立 "前序/中序/后序" 遍历序列。

根据 "前序/中序/后序" 遍历序列，建立二叉树。

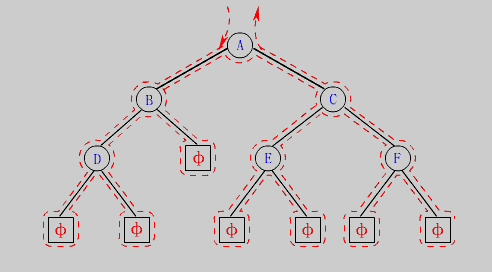
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

1. 前序遍历(Preorder Traversal，先序遍历)

访问顺序：根→左子树（根→左子树（……）→右子树）→右子树。

2. 中序遍历(Inorder Traversal)

访问顺序：左子树（根→左子树（……）→右子树）→根→右子树。

3. 后序遍历(Postorder Traversal)

访问顺序：左子树（根→左子树（……）→右子树）→右子树→根。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。

NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);

下面主要分析前序递归遍历，中序与后序图解类似，同学们可自己动手绘制。

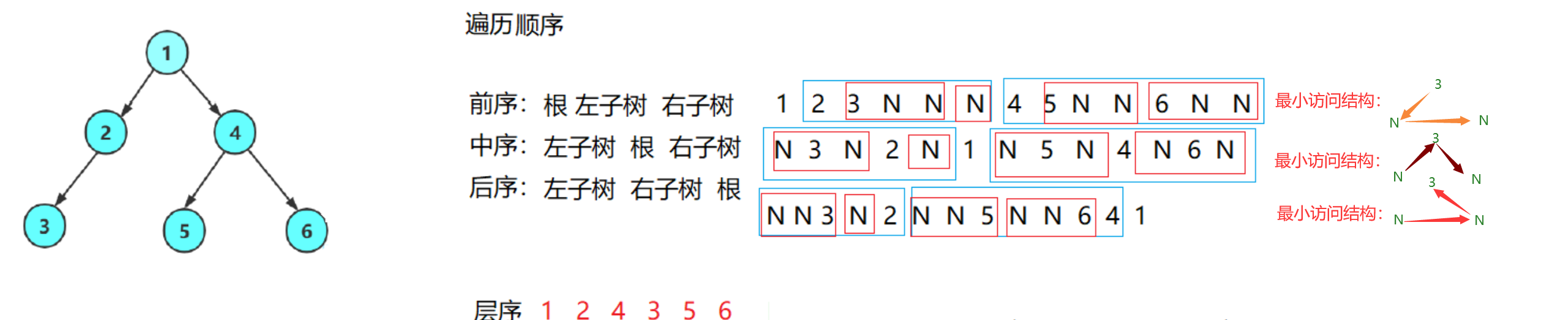
前序遍历递归图解：

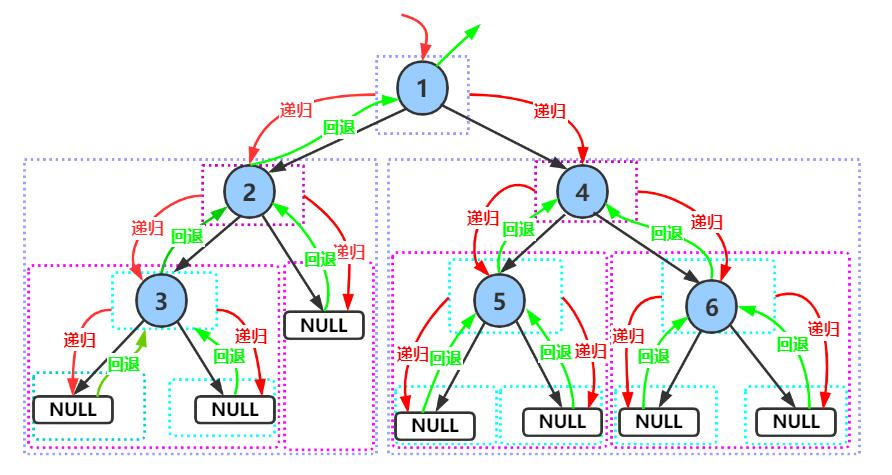
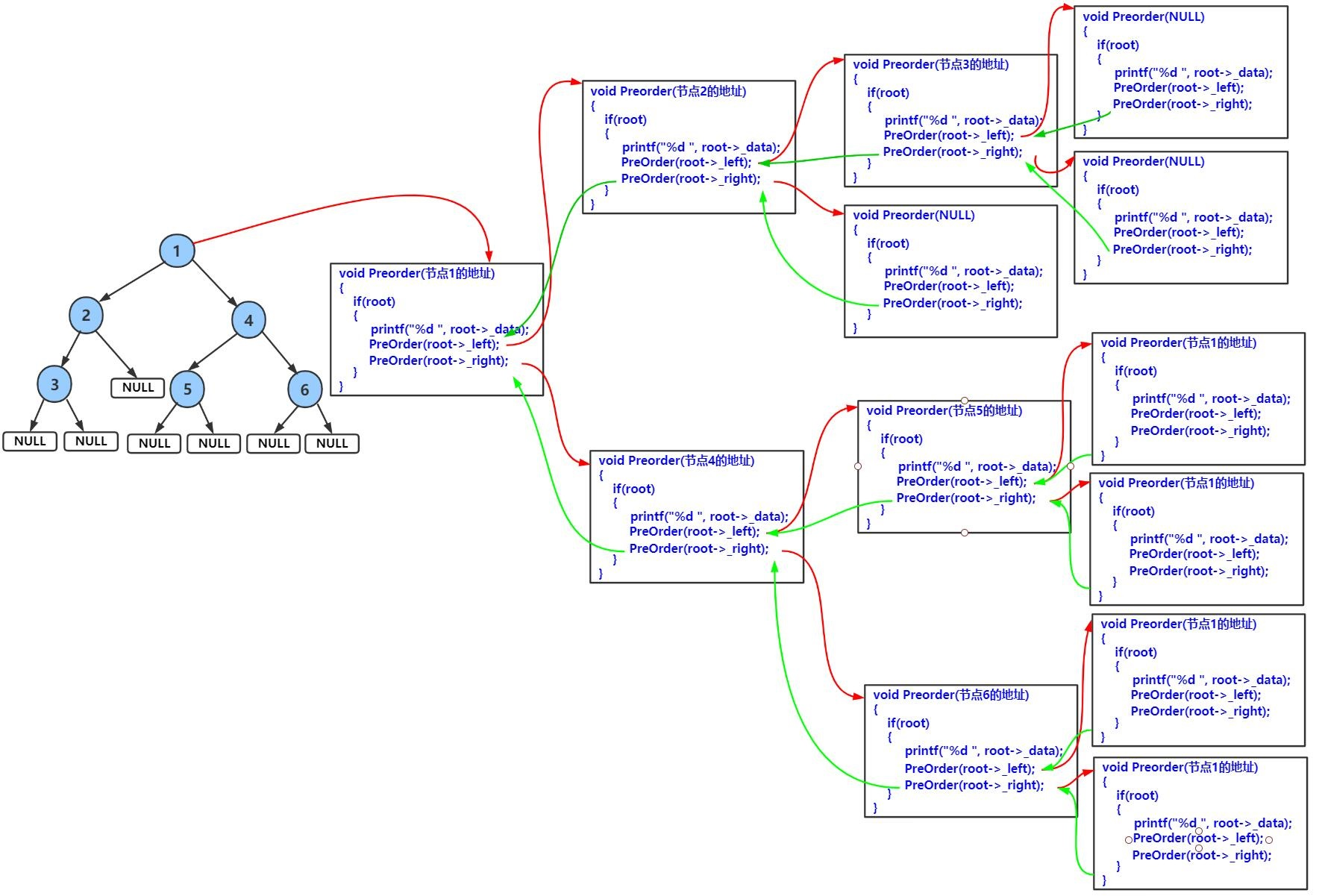
前序遍历结果：1 2 3 4 5 6
中序遍历结果：3 2 1 5 4 6
后序遍历结果：3 2 5 6 4 1

最小递归子问题：访问到空指针（空树）。

常规的数据结构的思路：

先创建一个数据结构（结构体）

再给一些接口——插入、删除……

节点个数、树的高度、……等

但是二叉树这里，增删查改没有价值，原因在于：
① 哪里都可以插入，有根类似于头，但是没有尾。
② 普通二叉树意义不大——结构复杂，用来存储数据意义不大。

学习二叉树主要是学习它的结构操作——前、中、后序遍历。

所以要在普通二叉树上增加一些特质，如左子树比右子树大——用于搜索（搜索二叉树），才有意义。

x.2 前序遍历·打印

递归的两要素

递归子问题

递归结束条件（最小子问题）

//前序遍历打印
void PreOrder(BTNode* root)
{
	//结束条件——最小子问题——空树
	if (root == NULL)
	{
		//打印空
		printf("N ");//也可以不打印空，直接打印1 2 3 4 5 6
		return;
	}
	//打印xx树的根
	printf("%d ", root->val);
	//先访问左子树
	PreOrder(root->left);
	//访问右子树
	PreOrder(root->right);
	//(双路递归)

	//返回值为void的函数的结束
    //1.return提前结束    
    //2.执行完自然结束
}

理解递归函数的方法——画递归展开图（函数栈帧的建立和销毁）

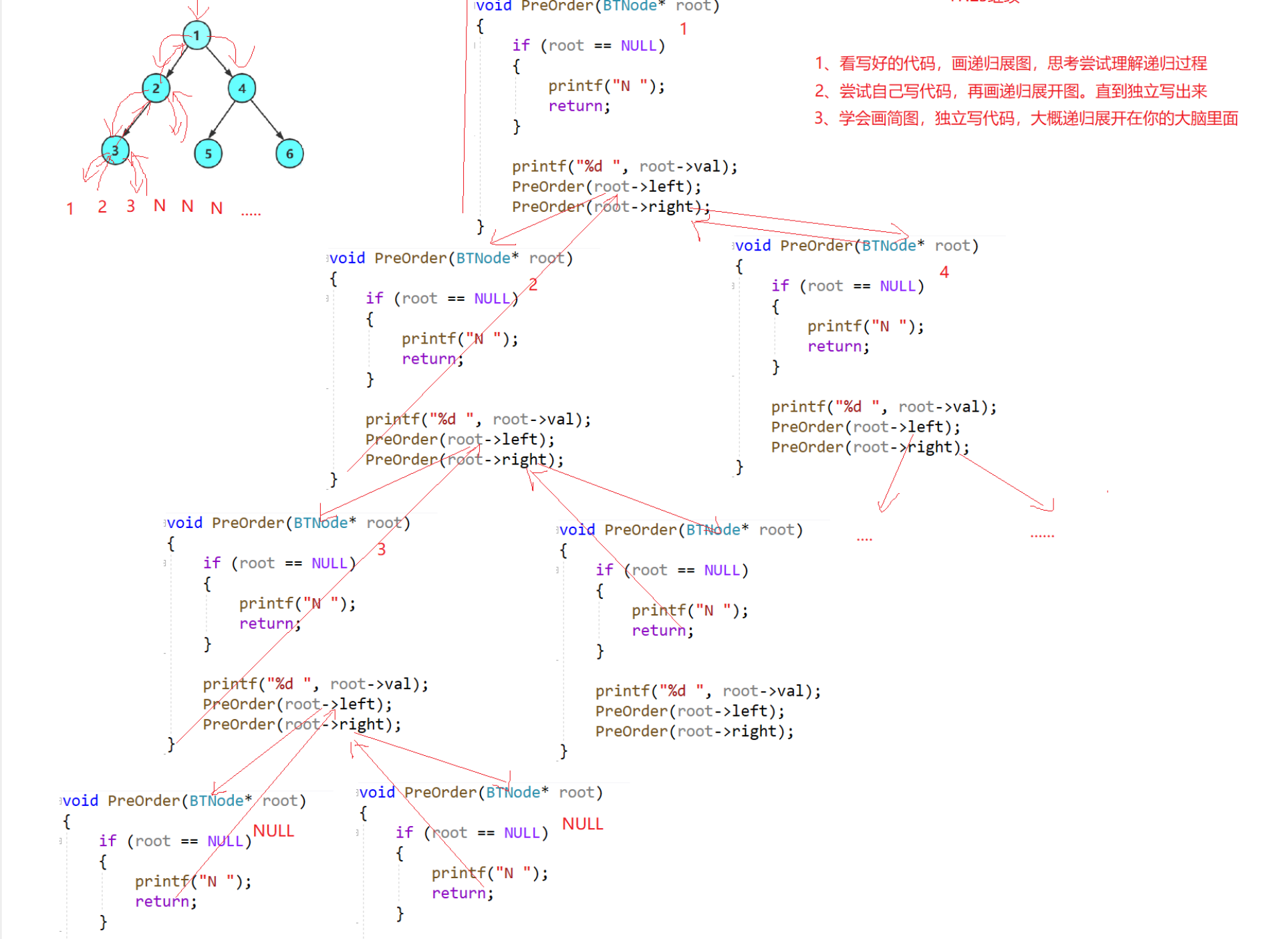
算法思想：回溯。

双路递归：右边的函数栈帧是复用左边的函数栈帧空间。

空间是可重复利用的。

所以递归的空间复杂度取决于递归的深度——完全二叉树才是logN，普通二叉树不是logN。

x.3 中序遍历·打印

我以为的中序：2 3 N N N 1 4 5 N N 6 N N——实际上还是前序的思想。

遇到1——不能访问，要先访问它的左子树。

访问左子树遇到2——不能访问，要先访问它的左子树。

继续访问左子树遇到3——不能访问，要先访问它的左子树。

继续访问左子树遇到NULL——访问左子树结束，退回上一步继续访问：根→右子树。

中序、后序——子问题(访问子树)嵌套子问题：最先执行出来的是最小子问题

本质区别：前序是先访问根——一个节点，可以直接访问。

中序、后序是先访问子树——一个树，需要针对子树再一次先访问子树。

前序：
整棵树的角度——1 左子树右子树
左子树的角度——2 左子树 N
右子树的角度——4 左子树右子树
底层结构的角度——3 N N

中序：
整棵树的角度——左子树 1 右子树
左子树的角度——左子树 2 N
右子树的角度——左子树 4 右子树
底层结构的角度—— N 3 N

//中序遍历打印
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

    //左
	InOrder(root->left);
    //根
	printf("%d ", root->val);
    //右
	InOrder(root->right);
}

理解递归函数的方法——画递归展开图（函数栈帧的建立和销毁）

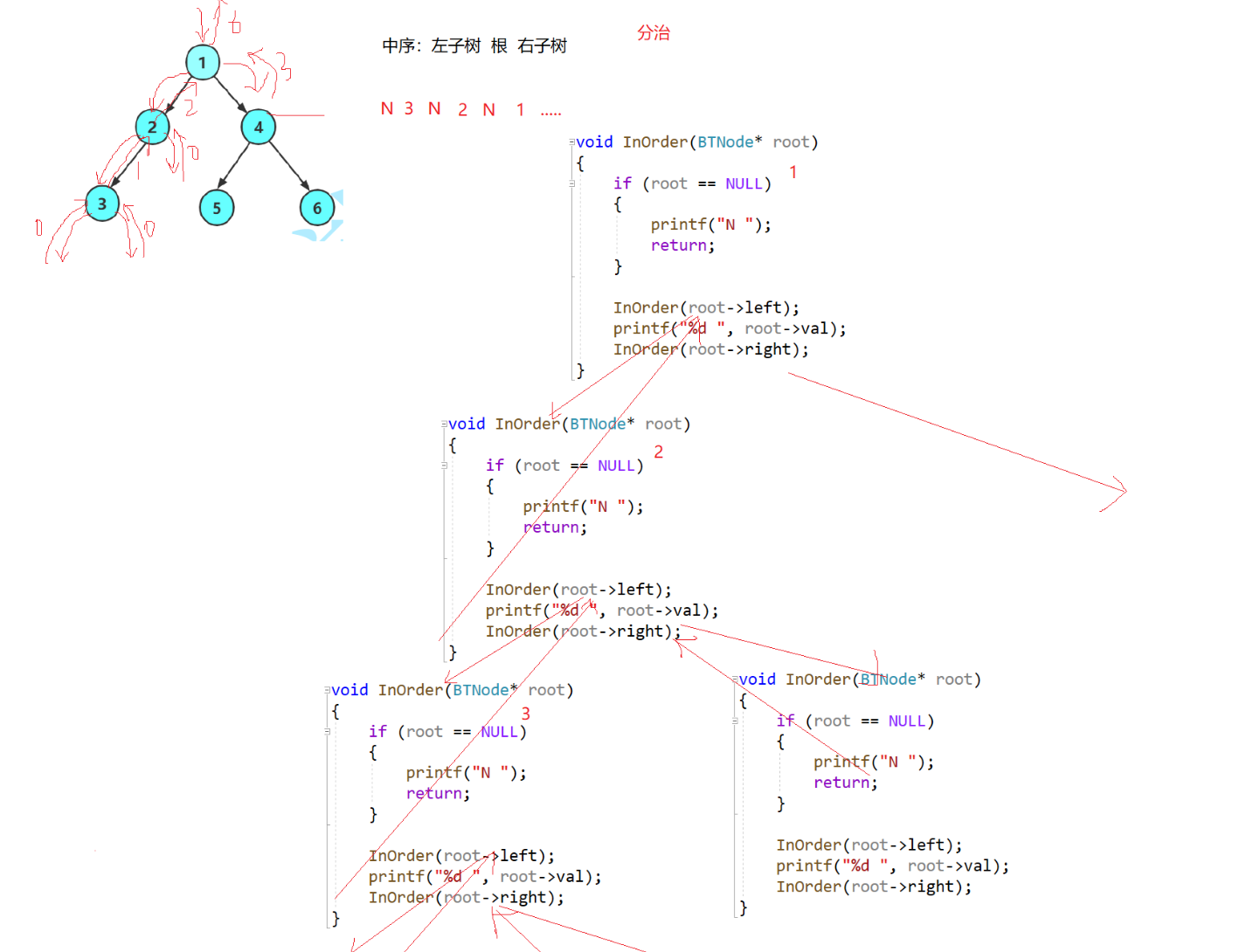
x.4 后序遍历·打印

代码实现。

//后序——遍历打印
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
    //左
	PostOrder(root->left);
    //右
	PostOrder(root->right);
    //根
	printf("%d ", root->val);
}

4.2.2 层序遍历

层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。

设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

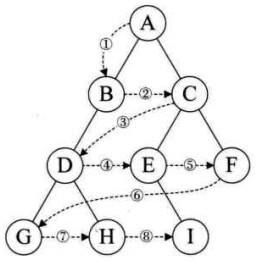
层序——一层一层走，不是递归，就可以不用管NULL。（二叉树中经典非递归）

x.5 层序遍历·打印

一层一层走，不用递归，一般是借助于队列——先进先出。（C语言得手搓）

思路：上一层带下一层→上一层的每一个根出队列的同时，带入自己的左右孩子。

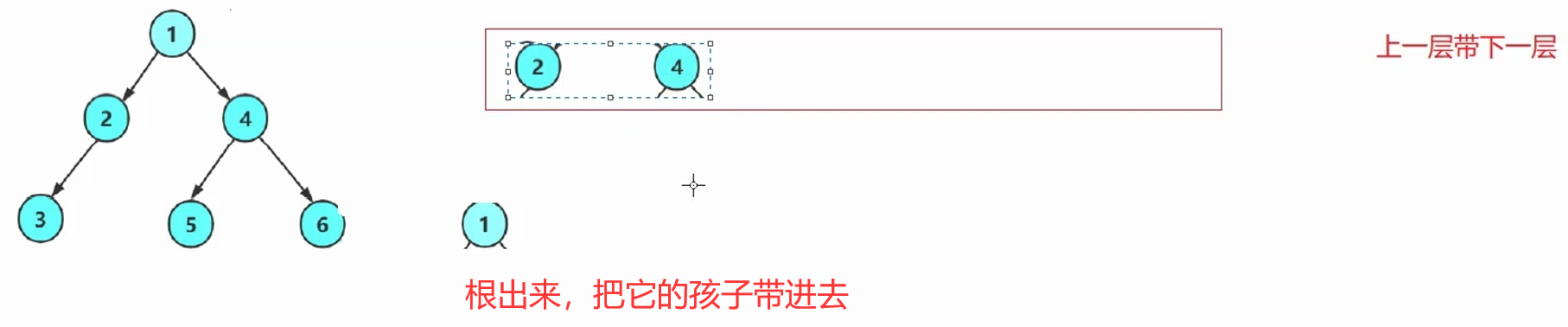
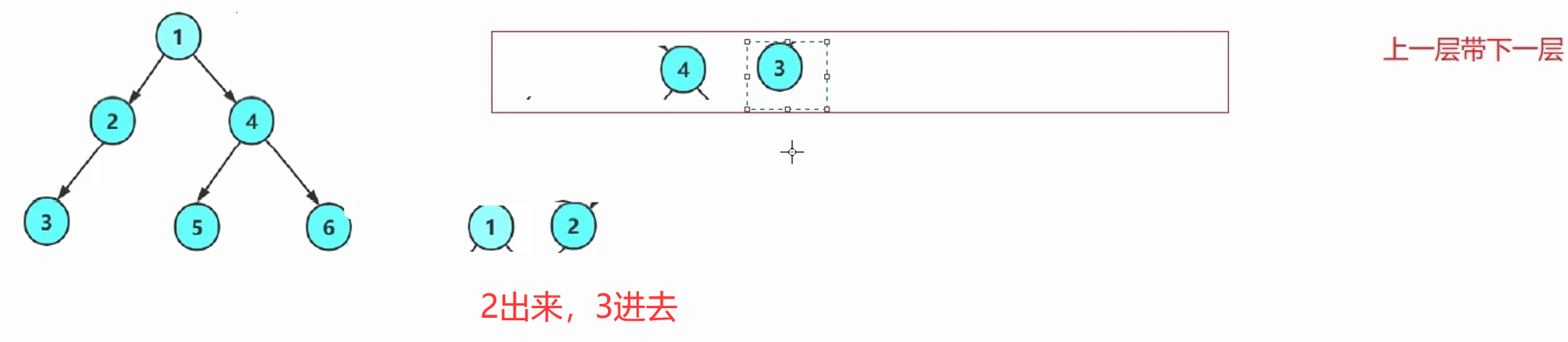
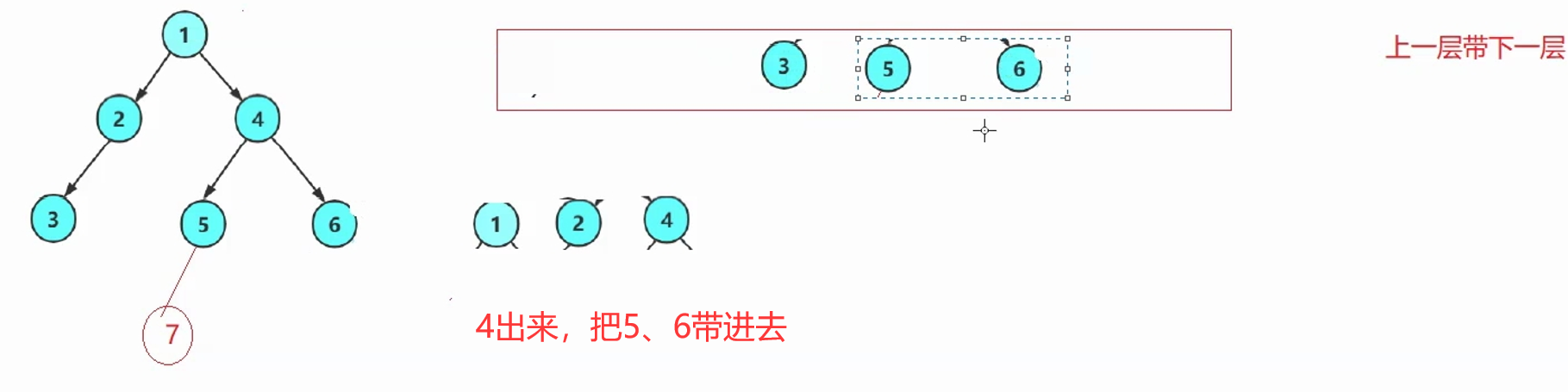
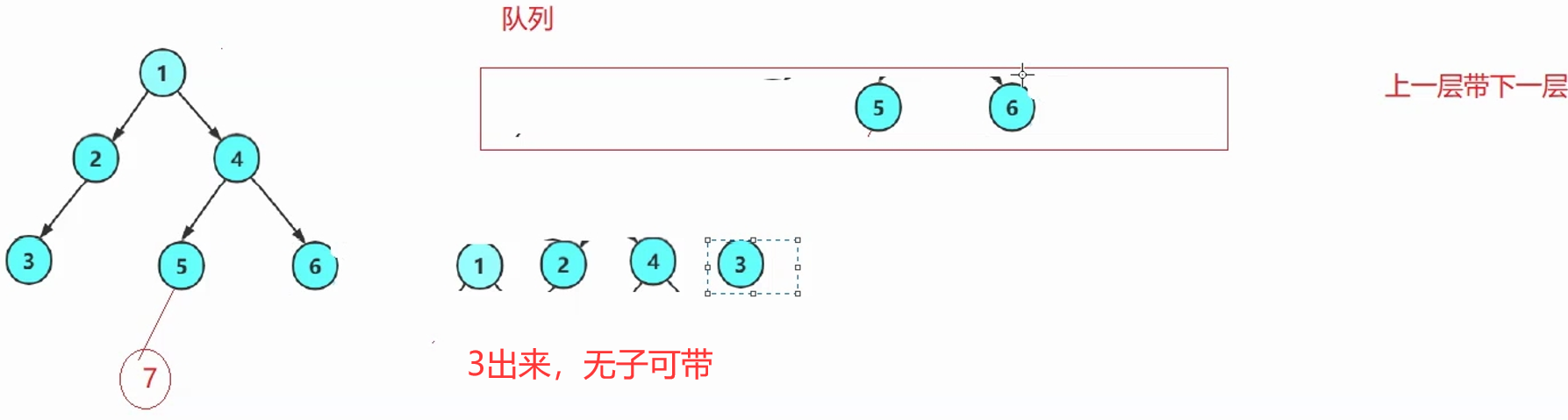
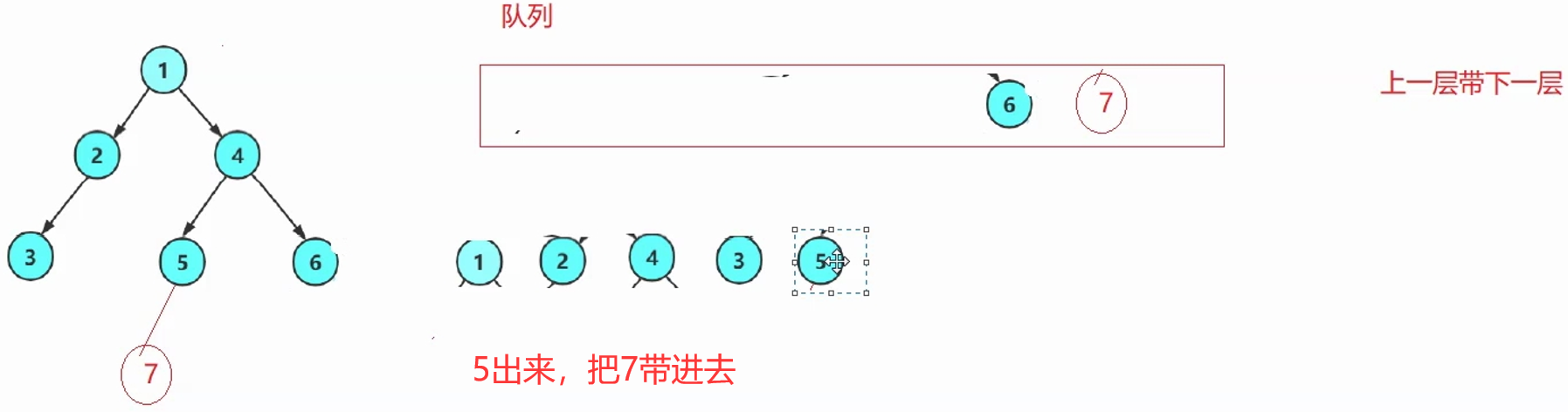
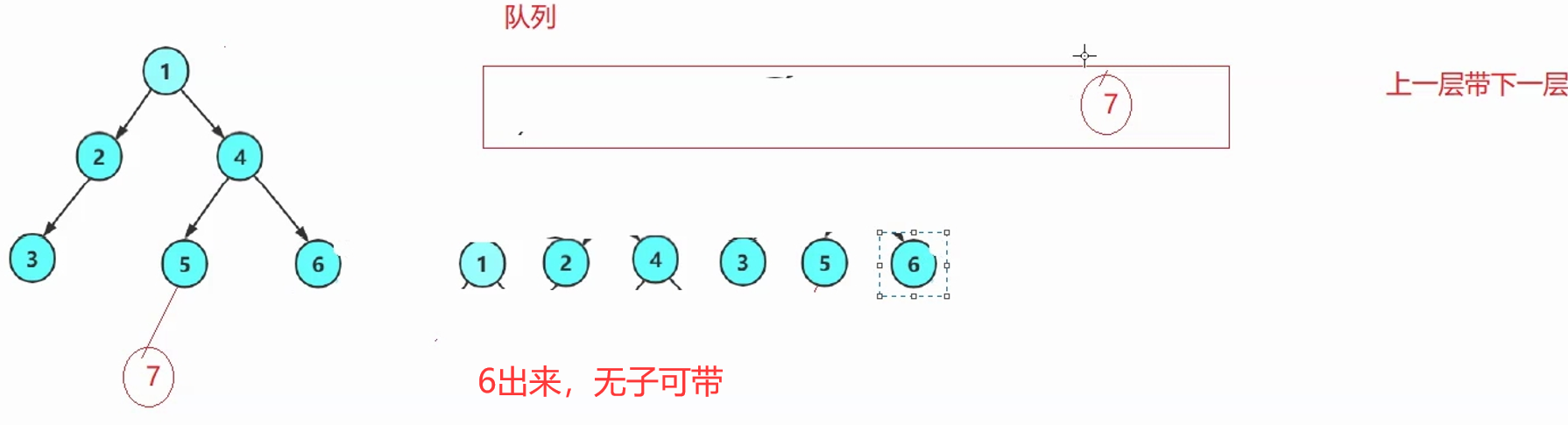
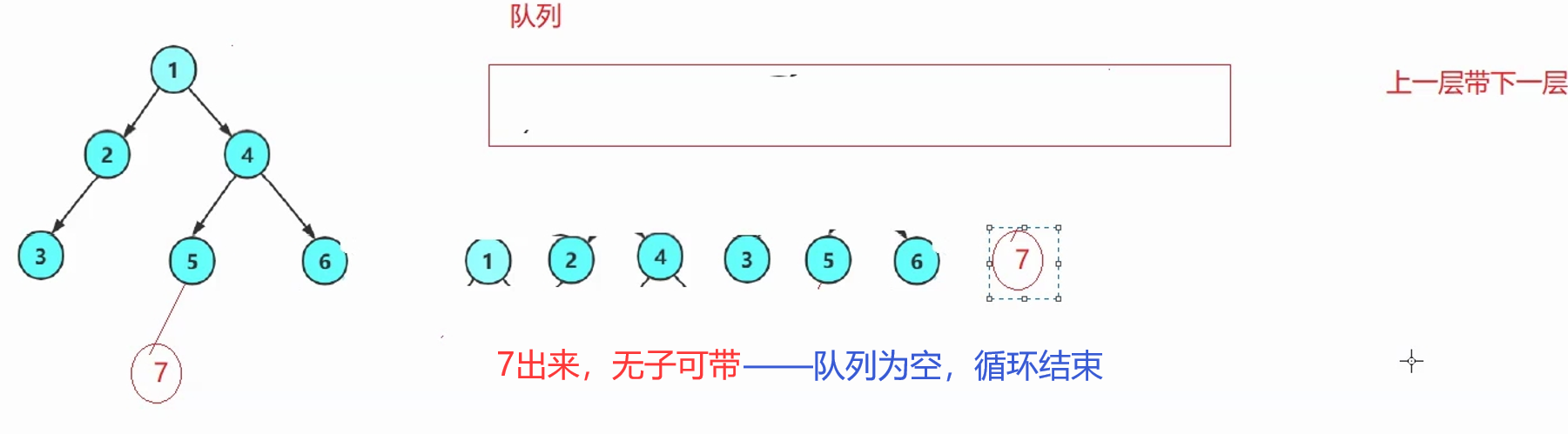
解释：每次循环，出队头结点，入队头结点的左右孩子。（空不入队列）

根作为种子一样，带入广大子孙。

插入队列的代码

把Queue.c、Queue.h拷贝到当前目录下。

修改队列的数据域，不再存储整型值，而是存储二叉树的节点，仅存值没法带入左右孩子。

存结点或结点的指针，优先选择存储结点的指针——越小越好。

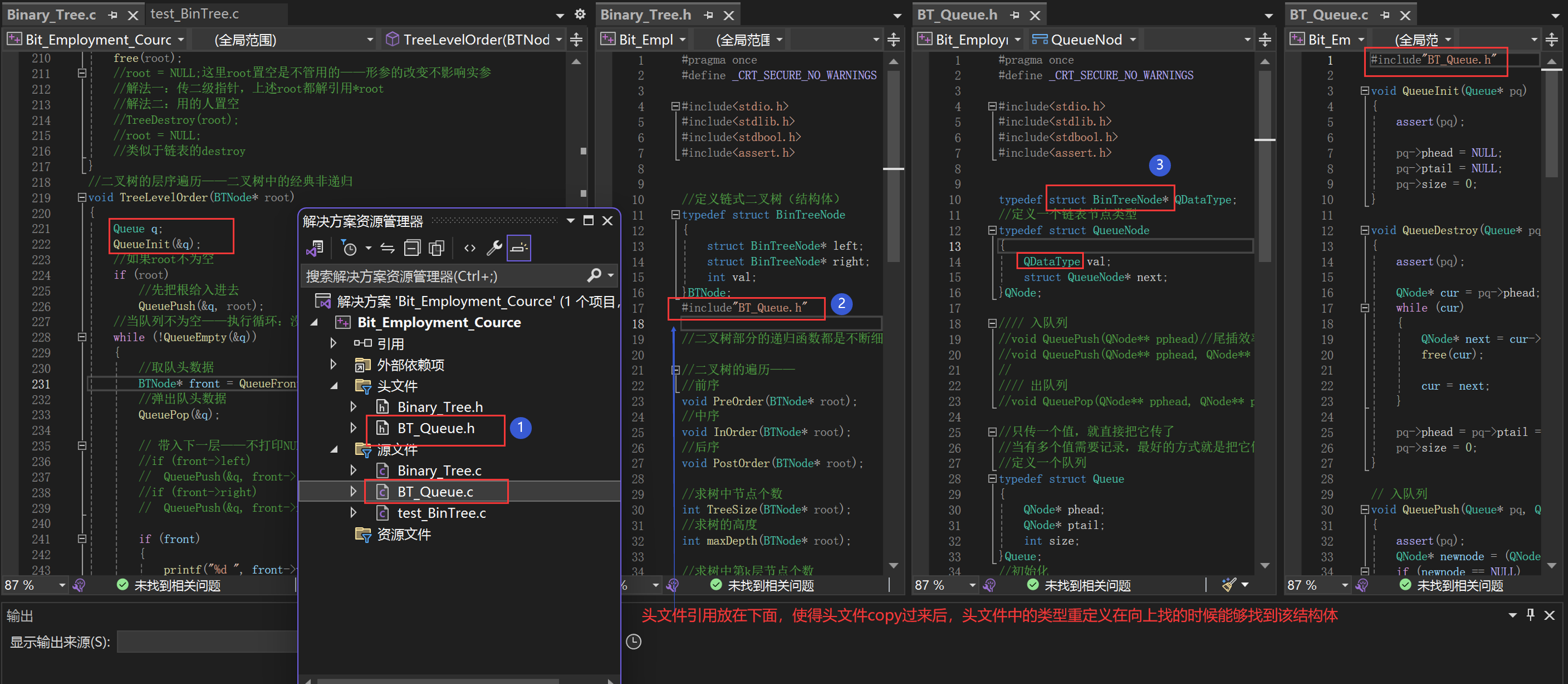
链接问题

不建议把函数实现放在.h头文件，而是选择声明和定义分离。

因为当把函数实现放在.h头文件，多个.c文件包含这个.h文件时会发生链接冲突。

error_LINK：xxx函数以在queue.obj中定义。（在tree.obj中也有）

头文件的嵌套包含的解决是在同一个.c文件包含多个头文件，头文件之间的嵌套包含。

层序遍历的代码。

// 二叉树的层序遍历
void TreeLevelOrder(BTNode* root)
{
    //创建队列、队列初始化
	Queue q;
	QueueInit(&q);

	//如果root不为空
	if (root)
		//先把根给入队列
		QueuePush(&q, root);

	//当队列不为空——执行循环：每次出一个，带入孩子
	while (!QueueEmpty(&q))
	{
		//取队头数据
		BTNode* front = QueueFront(&q);
		//弹出队头数据
            //pop会释放节点空间——释放的是队列节点
            //但是这个树结点本身还在，还能用地址front去访问、去打印
		QueuePop(&q);

        //队列不为空，才进循环，拿到队头front
        //不带NULL入队列，则拿到的front一定不为空
        //printf("%d ", front->val);  
        //  
		// 带入下一层——不打印NULL
		//if (front->left)
		//	QueuePush(&q, front->left);
		//if (front->right)
		//	QueuePush(&q, front->right);

        // 队头不是NULL
		if (front)
		{
			printf("%d ", front->val);

			// 带入下一层——空也进队列
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
        //队头是NULL
		else
		{
			printf("N ");
		}
	}
	printf("\n");

	QueueDestroy(&q);
}

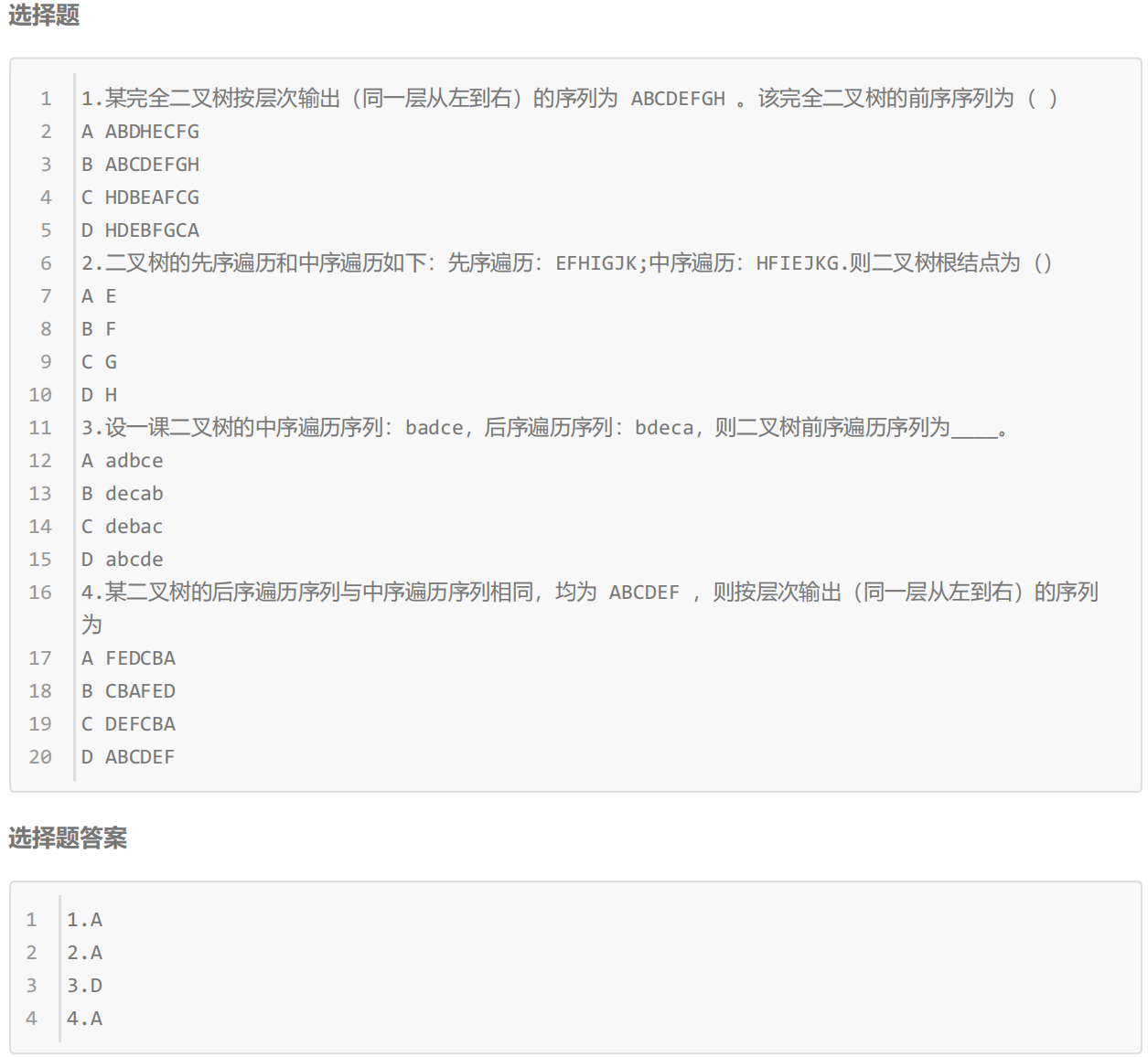
练习：请写出下面的前序/中序/后序/层序遍历

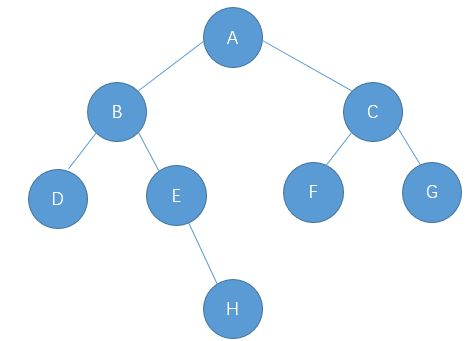
一般而言，二叉树遍历的结果都是不打印空的——打印能帮助更好地理解。

4.3 二叉树常用接口函数

节点个数、树的高度、……等

// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

x.6 二叉树的结点个数

思路1. 遍历一遍，用一个计数器

以链表的节点计数为例：

int Listsize(……)
{   
    int size = 0;          //计算链表的节点个数
    //……
}

只会有一个被调函数Listsize，局部变量size可以在这个函数内部随意使用。

二叉树的TreeSzie()会调用多个被调函数，而又希望每个被调函数都操作（++）同一个size变量。

注意

在递归函数内部定义计数器（变量），要定义成静态局部变量。

静态变量不在函数栈帧内部，在静态区。

静态成员变量只会被初始化一次。

int TreeSize0(BTNode* root)
{
    // 静态局部变量
	static int size = 0;     //此处的静态成员变量定义语句，只会被执行一次
	if (root == NULL)
		return 0;
	else
		++size;

	TreeSize0(root->left);
	TreeSize0(root->right);
	return size;
}

缺陷

调用一次printf("%d\n", TreeSize(root))返回6，调用两次返回12……调用n次返回6*n。

因为静态成员变量只会被初始化一次！！！

举例：

void func()
{
    static int x = 0;
    ++x;
}
//调试发现当第二次调用func函数时，黄色箭头直接跳过第一句，直接到达++x;
//静态成员变量只会被初始化一次

size在局部，只能初始化一次。

解决

把size定义语句移出函数内部，成为全局变量int size = 0;

或静态全局变量static int size = 0;

//计算二叉树结点数目
int size = 0;
int TreeSize1(BTNode* root)
{
    if (root == NULL)
        return 0;
    else
        ++size;

    TreeSize1(root->left);
    TreeSize1(root->right);
    return size;
}

那么就需要每次调用printf("%d\n", TreeSize(root))之前初始化一下size = 0;

void test()
{
    //……
    size = 0;
    printf("%d\n", TreeSize(root));
    size = 0;
    printf("%d\n", TreeSize(root));
    //……
}

缺陷

设置全局变量的方法有“线程安全”的风险——当TreeSize被多个线程调用，这个++size不是线程安全的。

更好的做法：执意要计数，还有一种方案——加传一个size的指针过来（只传size是拷贝），每次调用时“解引用”就都是这个局部变量。

//计算二叉树的结点个数
void TreeSize2(BTNode* root, int* psize)
{
	if (root == NULL)
		return 0;
	else
		++(*psize);

	TreeSize2(root->left, psize);
	TreeSize2(root->right, psize);
}

void test()
{
    //……
    int size = 0;
    TreeSize(root,&size)
    printf("%d\n", size);

    size = 0;
    TreeSize(root,&size)
    printf("%d\n", size);
    //……
}

局部变量在多线程之间就不会互相影响了，就是线程安全的了。

思路2——分治递归

最佳的解法——分治思想（递归）：分而治之。

类比：校长统计到校人数。

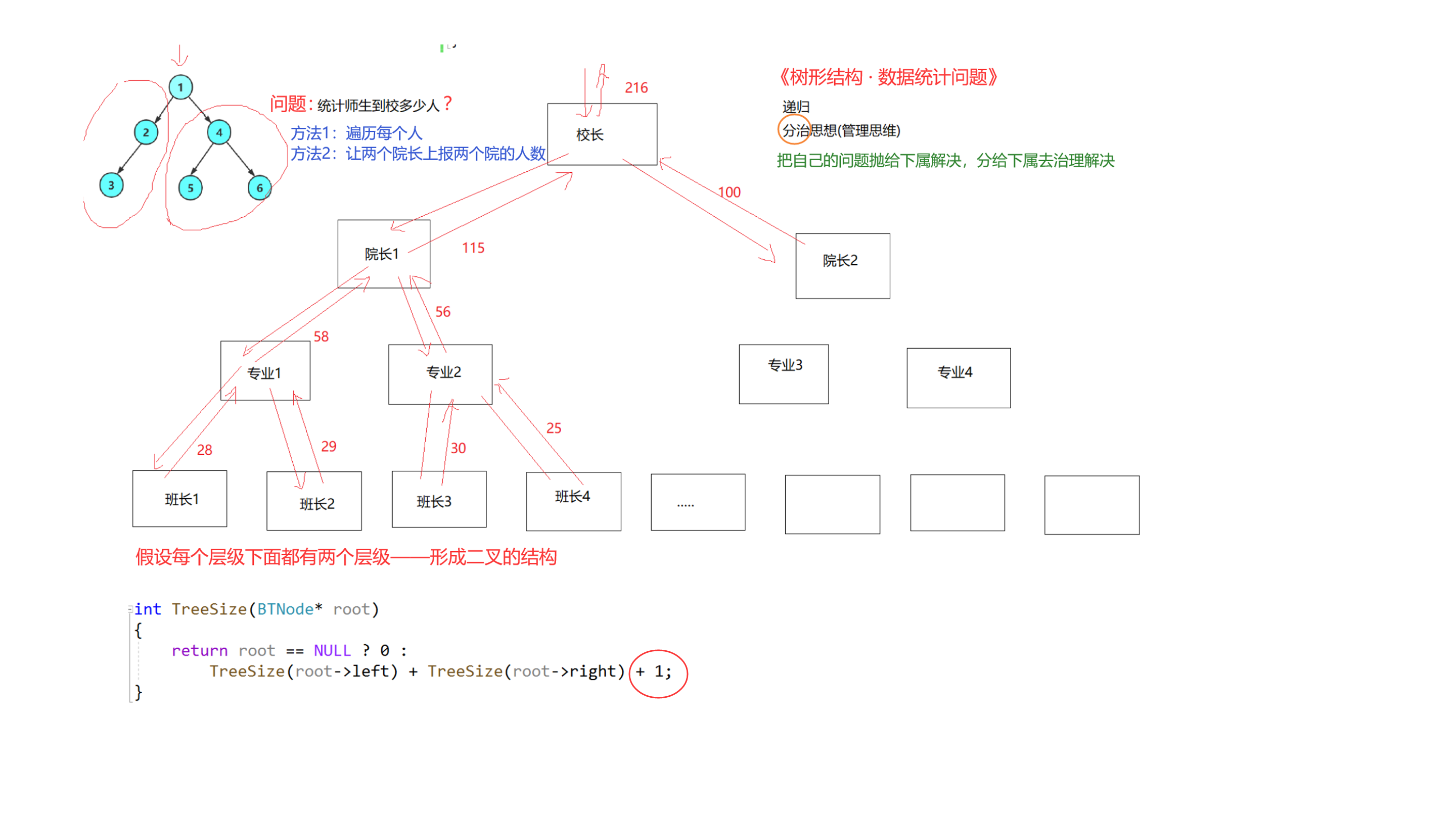
两要素

找出递归子问题、结束条件。

int TreeSize(BTNode* root)
{
    return root == NULL ? 0 :
        TreeSize(root->left) + TreeSize(root->right) + 1;
}

解释：是空树就返回0，不是空树就返回——左子树返回的节点个数 + 右子树返回的节点个数 + 1（自己这个节点）

左子树返回的节点个数 + 1 + 右子树返回的节点个数——不算中序。

1 + 左子树返回的节点个数 + 右子树返回的节点个数——不算前序。

还是需要把左右子树的节点个数算完，自己这个结点才能返回结点个数。

——经典后序（凡是求节点数、高度，都是后序——左树，右树走完才能算自己）。

x.7 二叉树的高度

求树的高度 == 层数 == 最长路径节点数 == 深度 == 最高（深）结点的高度（深度）。

类比：校长要调查学校最高的同学的身高。

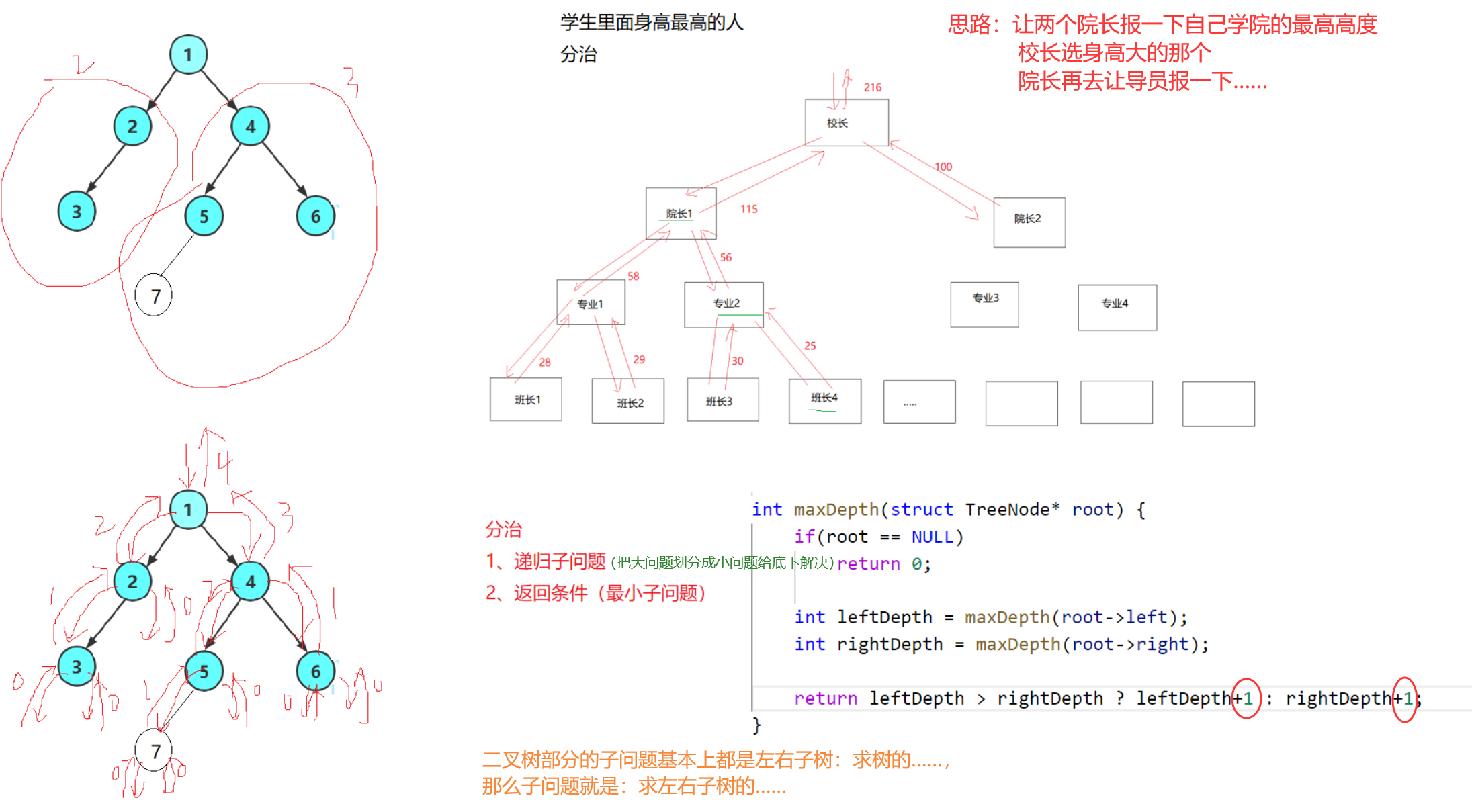
递归思路：从叶子开始，每个节点都返回自己节点开始的最长路径——经典后序。

求高度这里的最小子问题是什么：空 or 叶子？

如果把最小子问题定为叶子：

if (root->left == NULL && root->right == NULL) 
    return 1，

则不能包含所有子问题：

5不是叶子，就要去调左、右子树判断是不是叶子，调右子树判断是不是叶子会出现访问空指针。

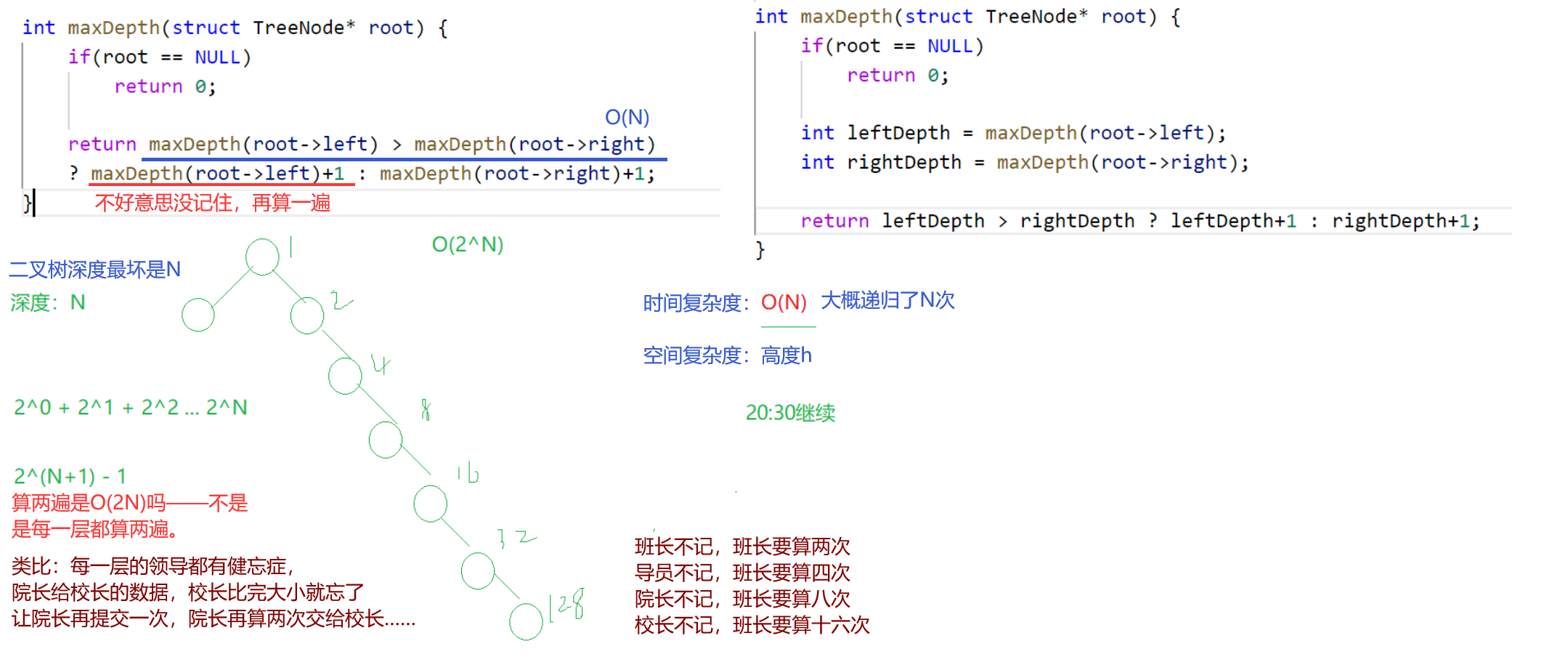
//二叉树的高度
int TreeHeight(BTNode* root)
{
	//最小子问题：叶子的左树和右树——空
	if (root == NULL)
		return 0;
	
    //1.求出左子树的高度
	int leftDepth = maxDepth(root->left); 
    //2.求出右子树的高度
	int rightDepth = maxDepth(root->right);
    //3.求出本节点的高度
	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
    
    //凡是比较后再使用变量值的，最好使用变量存储，而不是直接使用函数的返回值
    //这样可以减少一次函数调用
}

而且这里，只能使用变量存储。

~~因为是递归调用，每次函数调用不一样。~~

写法每次，力扣过不了因为性能没过——执行超时。

x.8 二叉树第k层节点数

递归思路

① 递归子问题：左子树的k层结点数 + 右子树的k层结点数。

② 结束条件：第k层结点，返回1。

二叉树部分的递归子问题基本上都是左右子树：

求树的........，那么子问题就是：求左右子树的........。

~~定义一个层数变量，每往下一层就自增1。~~

跟求结点个数一样，定义变量的方式在递归函数中不太好。

所以选择将层数变量设置成函数的参数。

递归子问题

当前树的第k层结点个数 = 左子树的第k-1层结点个数 + 右子树的第k-1层结点个数

结束条件

二叉树部分的最小子问题一般而言，空NULL都算一个最小子问题

这道题还有一个结束条件就是 k = 1

//求解1——二叉树k层节点
int TreeKLevel(BTNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	
	if (k == 1)
		return 1;

	// 不等于空 && k > 1
    // 说明第k层的节点在子树里面，转换成子问题求解
	// 
	//int left = TreeKLevel(root->left, k - 1);
	//int right = TreeKLevel(root->right, k - 1);
	//return left + right;

    //没有比较，直接使用函数返回值——没有二次调用，就不需要使用变量存储
	return TreeKLevel(root->left, k - 1)
		+ TreeKLevel(root->right, k - 1);
}

比较完不记录结果，就会有二次调用，对较上层的结点的函数调用2次，对较下层的结点的函数就要调用2的指数次。

（上头一句话，下头跑死马——层层加码）

不能交换两个判断的位置。

	if (k == 1)
		return 1;

	if (root == NULL)
		return 0;

例：对一个有左叶子、没有右叶子的节点（假设此时k=2），那么去调用这个结点的左子树（k=1）就返回1，调用右子树（k=1）也返回1，没有返回0。

x.9 查找

查找二叉树指定值的结点指针——查找第一个值为x的结点。（而后就能执行修改功能）

递归思路

递归子问题

当前结点不是我们要找的 => 左子树里面找 + （左子树没找到）右子树里面找

（前序思想）

结束条件

二叉树部分的最小子问题一般而言，空NULL都算一个最小子问题（找不到了）

这道题还有一个结束条件就是 val = x（找到了）

先走左树、先走右树没区别，因为你不知道数据在左树的概率大，还是在右树的概率大。

代码1——以递归的思路写代码

//查找x结点——代码1
BTNode* TreeFind(BTNode* root, int x)
{
	if (root == NULL)
		return NULL;

	if (root->val == x)
		return root;

	TreeFind(root->left, x)
    TreeFind(root->right, x);
}

错误点：主函数没有返回。

子树找到了root，返回root，最外面能拿到吗？一>不能

返回不是返回给最外面，而是返回给调用的地方，调用的地方没接收，返回值就丢了。

而这里上一层调用函数的地方没有接收——>值就丢了，然后继续去右边找。

无论在右边找到找不到，都是又不接收，丢了，实际上最外层函数没有返回值，返回的是随机值。

严格一点，会报警告（VS），甚至报错（力扣）。

代码2。

//查找x结点——代码2
bool TreeFind(BTNode* root, int x)
{
	if (root == NULL)
		return NULL;

	if (root->val == x)
		return true;

	return TreeFind(root->left, x)
        || TreeFind(root->right, x);
}

缺陷：只能查找有没有x这个值——查找在不在。（没法返回在哪里，无法执行修改）

代码3。

//查找x结点——代码3
BTNode* TreeFind(BTNode* root, int x)
{
	//本结点
	if (root == NULL)
		return NULL;

	if (root->val == x)
		return root;

	//if (TreeFind(root->left, x))
	//	return TreeFind(root->left, x);
	//找到了，不保存结果，就要找第二次——典型的二次调用
    //树形结构递归往下的二次调用的消耗是指数级的

	//左子树
	BTNode* ret1 = TreeFind(root->left, x);
	if (ret1)
		return ret1;
	//右子树
	BTNode* ret2 = TreeFind(root->right, x);
	if (ret2)
		return ret2;

	//本结点没找到 && 左右子树都没有找到
    //就返给上一层节点——表示上一层的 左 或 右子树 没有找到
	return NULL;
}

举例：查找3——递归展开图

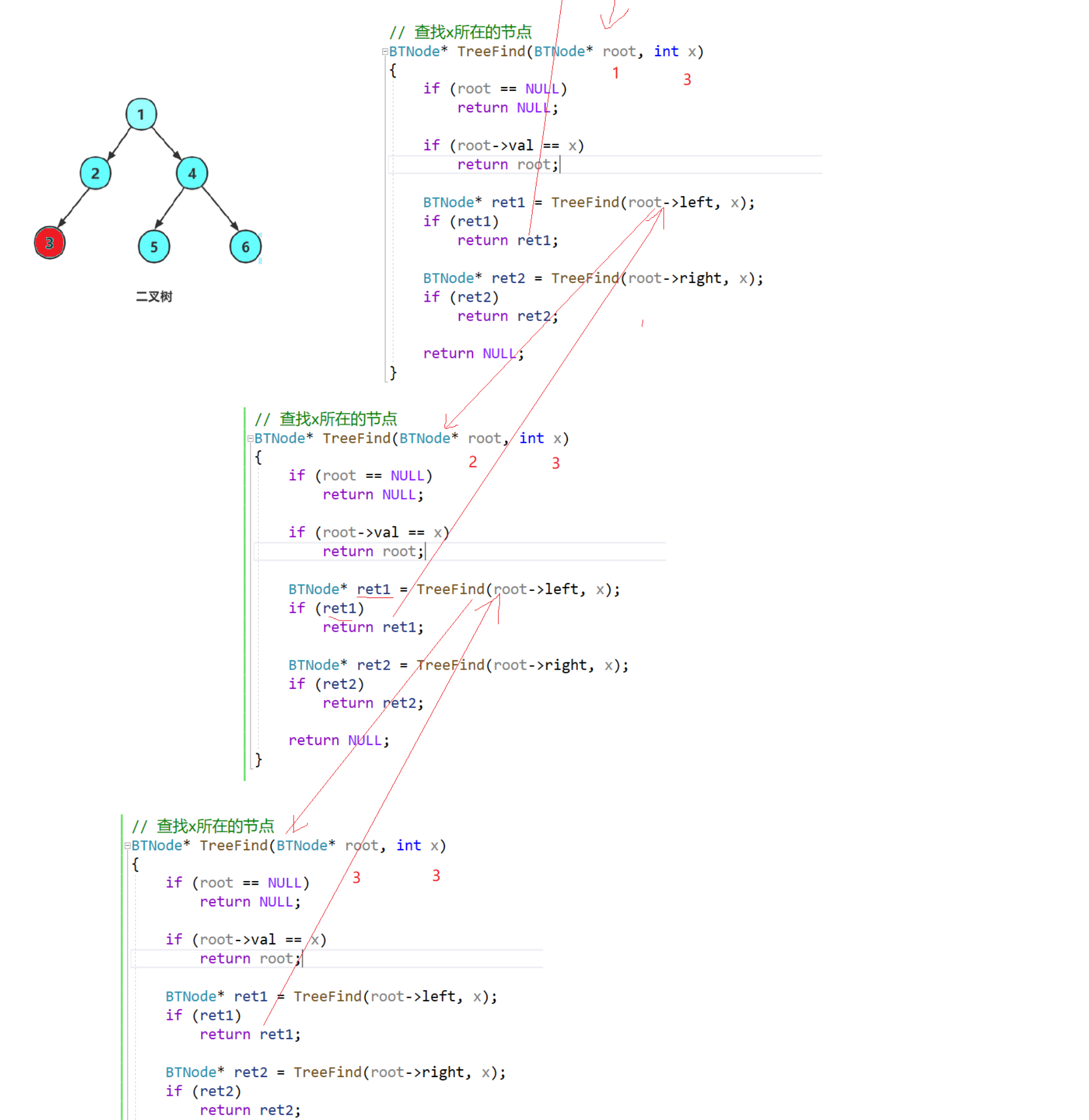
查找的返回值是层层往回返的，return是return给上一层的。

举例2：查找4——递归展开图

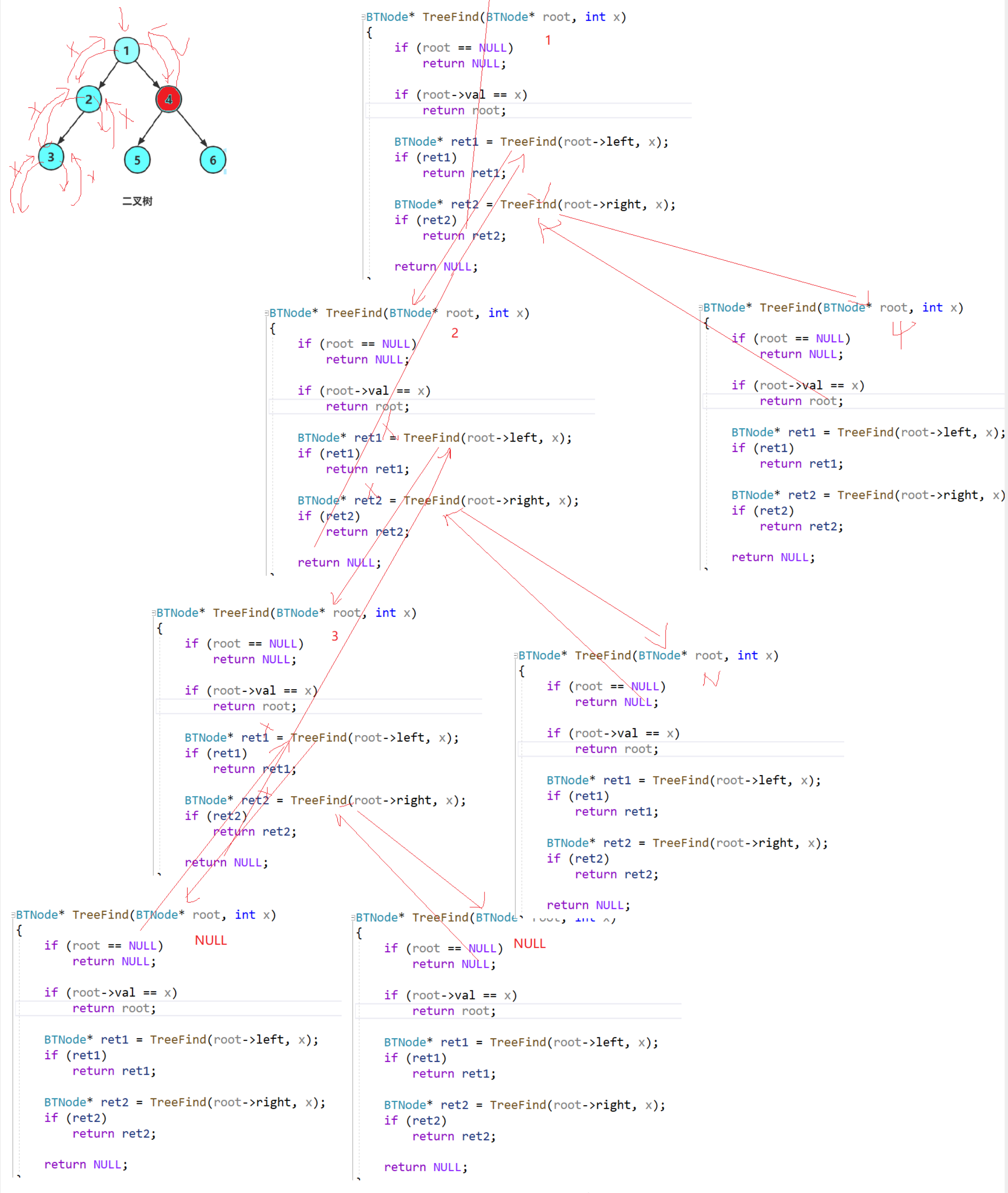
代码4——代码3的简化（可读性没代码3好）

//查找x结点——代码4
BTNode* TreeFind(BTNode* root, int x)
{
	if (root == NULL)
		return NULL;

	if (root->val == x)
		return root;

	BTNode* ret1 = TreeFind(root->left, x);
	if (ret1)
		return ret1;

	return TreeFind(root->right, x);
}

左子树找到了，就返回左根；

左子树没找到，那么不管右子树找到找不到，都返回右子树的查找结果。

类比：x & 1、x | 0，表达式的结果取决于x——与、或门的特点

数据结构初阶（9）二叉树链式结构的实现