题解：P11140 [APC001] E - Linear Map_双指针_dp优化_C++_算法竞赛

https://www.luogu.com.cn/problem/P11140

推销洛谷博客：https://www.luogu.com.cn/article/07909wbm

遇到计数题，不是排列组合就是 dp。这道题显然是 dp。

考虑如何设计状态，序列划分问题有通用状态：设当前位置、上一次的分割点、分的段数、最后一段的信息等。

对于本题，由于不考虑段数和其他信息，不妨先简单地设 $d{p}_i$ 表示前 $i$ 个位置的分段方案数。

定义若 $[j,i]$ 有趣，则 $\text{check}(j,i)$ 为真。

转移类似最长上升子序列，考虑枚举前一次的分段位置 $j(j<i)$，若 $[j,i]$“有趣”则可以转移：
$$f_i=\sum _{1\le j\le i}{f}_{j-1}\cdot [\text{check}(j,i)]$$
（从 $j-1$ 转移是因为我们把位置 $j$ 也算作当前段的一部分）。

这样加上判定时间复杂度是 $O(n^4)$ 的，其中 $\text{check}$ 函数的时间复杂度就占了 $O(n^2)$，考虑优化判定函数和 dp 转移。

先优化判定函数。

判定函数的关键就是用一个桶去重，优化思路大体应该是看看能不能在遇到每个新位置时利用一下旧的桶数组，从而减少运行次数。

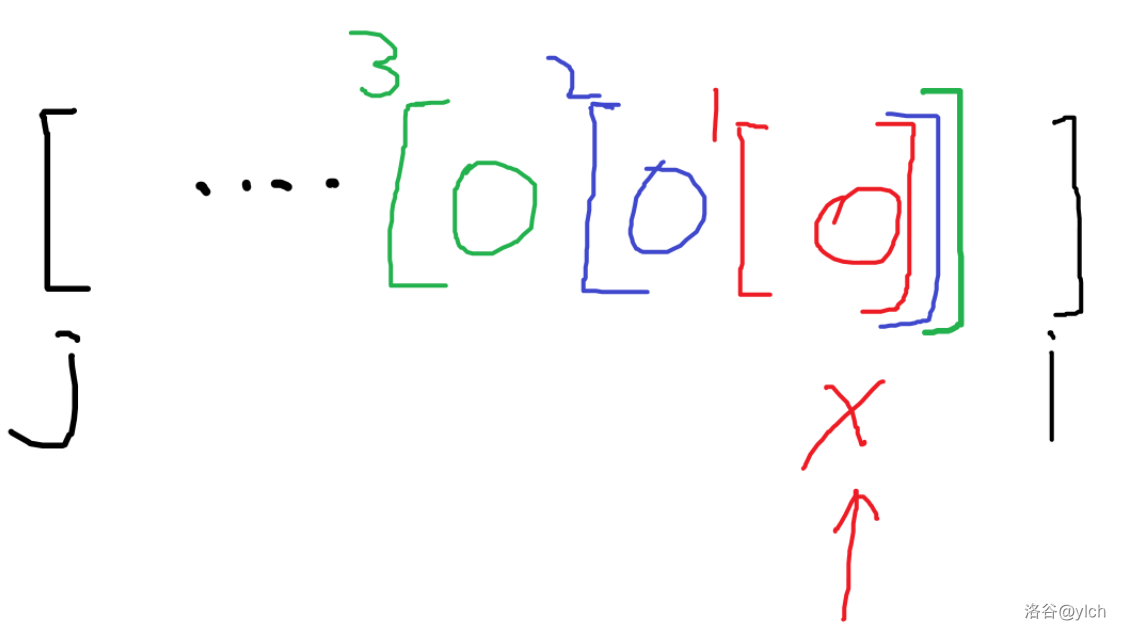
画个图，假设当前枚举到区间 $[j,i]$，发现每增加一个新位置 $x$，新出现的区间都是由这个新位置和其前面的一个连续区间 $[x-1,k]$ 拼成，那么我们不妨在转移时从后往前枚举 $k$，这样不就能利用之前的桶数组减少时间开销了吗？

注意题目中判定要求是“两段长度均 $>1$ 的不同区间”。

$\text{check}O(n)$，总时间复杂度 $O(n^3)$：

void solve()
{
	cin >> s; int n = s.size(); s=' '+s;
	for(int i = 1; i <= n; i ++){
		sum[i] = sum[i - 1] + (s[i] - '0');
	}
		
	dp[0] = 1; // 表示空串也是1个方案（用来转移[1,i]全选的状态）
	for(int i = 1; i <= n; i ++){
		unordered_set<ll> vis; // 桶数组，用来判重（放在这里便于复用）
		auto check = [&](int l, int r){
			if(l == r) return true;
			for(int k = l + 1; k <= r; k ++){ // 从l+1开始枚举是因为题目说长为1的段不算重复
				if(vis.count(sum[k] - sum[l - 1])) return false;
				vis.insert(sum[k] - sum[l - 1]);
			}
			return true;
		};
		
		for(int j = i; j >= 1; j --){ // 转移，倒叙枚举以减小复杂度
			if(check(j, i)){
				dp[i] = (dp[i] + dp[j - 1]) % mod;
			}
		}
	}
	cout << dp[n] << '\n';
}

下面优化 dp 转移。

想化简好像只能从 $\text{check}(j,i)$ 入手。

打印一下，我们惊奇地发现 $\text{check}(j,i)$ 竟然满足单调性！即对于一个固定的 $i$，存在一个分界点 $j$，使得 $1\sim j-1$ 之间的位置都满足 $\text{check}$ 为假，$j\sim i$ 之间的位置 $\text{check}$ 为真。

单调性证明：如果一个区间“无趣”，包含这个区间的大区间肯定也“无趣”，满足单调性。

既然这样，考虑用双指针，枚举每一个右端点 $r$（就是前文中的 $i$），并找到最小的使 $[l,r]$ 有趣的 $l$ 进行转移。

但因为端点的枚举逻辑变了，所以修改和撤销桶数组的方式也要变。

重新从左端点枚举到右端点肯定是来不及了，那么考虑每次从端点处向左右延申，这样就能匹配上双指针的操作了。（详见代码）

最后，由于 $l$ 单调不降，所以时间复杂度可以做到 $O(n^2)$。

最后的最后，根据其他题解通过爆搜可以得出“有趣”字符串的最大长度只有 $9$！所以我们转移时 $j$ 与 $i$ 的距离一定不会超过 $9$。常数忽略不计，时间复杂度就是线性 $O(n)$ 的了。

好题呀！！！

注：本题需要卡常。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1.5e7 + 7, mod = 998244353;

string s;
ll dp[maxn];

int vis[maxn + 1000]; // 桶数组，用来判重（不要用map）
int same = 0; // 存当前重复的段个数（是否有重复）

void solve()
{
	cin >> s; int n = s.size(); s=' '+s;
	
	dp[0] = 1; // 表示空串也是1个方案（用来转移[1,i]全选的状态）
	int l = 1; // 左端点
	for(int r = 1; r <= n; r ++){
		// 扩展左端点+撤销
		while(same && l < r){ 
			int cnt = s[l] - '0'; // 因为题目说和重复的段长度必须>1
			l ++;
			for(int k = l; k <= r; k ++){
				cnt += s[k] - '0';
				same -= ((vis[cnt]--) == 2); // 卡常
			}
		}
		
		// dp转移
		for(int k = r; k >= l; k --){ 
			dp[r] += dp[k - 1];
			if(dp[r] >= mod) dp[r] -= mod; // 卡常
		}
		if(r == n) break; // 防止后面的更新部分越界
		
		// 更新r+1
		int cnt = s[r + 1] - '0';
		for(int k = r; k >= l; k --){ 
			cnt += s[k] - '0';
			same += ((++vis[cnt]) == 2); // 卡常
		}
	}
	
	cout << dp[n] << '\n';
}

signed main()
{
	ios :: sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
	solve();
	return 0;
}