最后一天!!!
小明逛公园(Floyd算法精讲)
【题目描述】
小明喜欢去公园散步,公园内布置了许多的景点,相互之间通过小路连接,小明希望在观看景点的同时,能够节省体力,走最短的路径。
给定一个公园景点图,图中有 N 个景点(编号为 1 到 N),以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。
小明有 Q 个观景计划,每个计划都有一个起点 start 和一个终点 end,表示他想从景点 start 前往景点 end。由于小明希望节省体力,他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。
【输入描述】
第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。
接下来的 M 行,每行包含三个整数 u, v, w,表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。
接下里的一行包含一个整数 Q,表示观景计划的数量。
接下来的 Q 行,每行包含两个整数 start, end,表示一个观景计划的起点和终点。
【输出描述】
对于每个观景计划,输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径,则输出 -1。
【输入示例】
7 3
2 3 4
3 6 6
4 7 8
2
2 3
3 4
【输出示例】
4
-1
【提示信息】
从 2 到 3 的路径长度为 4,3 到 4 之间并没有道路。
1 <= N, M, Q <= 1000.
1 <= w <= 10000.
本题采用动态规划解决,单看代码是非常简单的,重点是理解原理。
1.确定dp数组及其下标的含义:
dp[i][j][k]=m表示节点i到节点j以[1...k]集合中的一个节点为中间节点的最短距离为m。
2.确定递推公式:
两种情况:
节点i到j的最短路径经过节点k:dp[i][j][k]=dp[i][k][k-1]+dp[k][j][k-1];
节点i到j的最短路径不经过节点k:dp[i][j][k]=dp[i][j][k-1]。
所以递推公式:dp[i][j][k] = min(dp[i][k][k - 1] + dp[k][j][k - 1], dp[i][j][k - 1])。
3.初始化:
对于输入的数据节点u,节点v,权值val,初始化dp[u][v][0]=val;
数组中其它元素的初始值为10001,因为题目给出边的最大距离为10000。
4.确定遍历顺序:
根据递推公式dp[i][j][k] = min(dp[i][k][k - 1] + dp[k][j][k - 1], dp[i][j][k - 1]),我们可以看出k是依赖于k-1的,而i和j并不依赖于i-1和j-1。
所以三维数组dp的遍历顺序是从底层一层一层往上的,也就是要先遍历k,i和j的遍历顺序无所谓。
空间优化:
我们可以发现,k只是依赖于k-1的状态,而不需要记录k-2,k-3等等这些状态。
也就是说,我们只要记录一个dp[i][j][0]和dp[i][j][1]就可以了,二者交替滚动。
再进一步想,就算在本层计算dp[i][j]用了本层中刚计算好的dp[i][j]会有什么问题吗?
如果 本层刚计算好的 dp[i][k] 比上一层 (即k-1层)计算的 dp[i][k] 小,说明确实有 i 到 k 的更短路径,那么基于 更小的 dp[i][k] 去计算 dp[i][j] 没有问题。
如果 本层刚计算好的 dp[i][k] 比上一层 (即k-1层)计算的 dp[i][k] 大, 这不可能,因为这样也不会做更新 dp[i][k]的操作。
所以在本层计算中,使用了本层计算过的 dp[i][k] 和 dp[k][j] 是没问题的。
所以递归公式可以写为:dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])。
代码如下:
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner in=new Scanner(System.in);
int n=in.nextInt();
int m=in.nextInt();
int[][] dp=new int[n+1][n+1];
for(int i=0;i<=n;i++){
for(int j=0;j<=n;j++){
dp[i][j]=10001;
}
}
for(int i=0;i<m;i++){
int u=in.nextInt();
int v=in.nextInt();
int w=in.nextInt();
dp[u][v]=w;
dp[v][u]=w;
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dp[i][j]=Math.min(dp[i][j],dp[i][k]+dp[k][j]);
}
}
}
int q=in.nextInt();
for(int i=0;i<q;i++){
int start=in.nextInt();
int end=in.nextInt();
if(dp[start][end]!=10001)System.out.println(dp[start][end]);
else System.out.println(-1);
}
}
}骑士的攻击(A*算法)
题目描述
在象棋中,马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标,要求根据骑士的移动规则,计算从起点到达目标点所需的最短步数。
骑士移动规则如图,红色是起始位置,黄色是骑士可以走的地方。
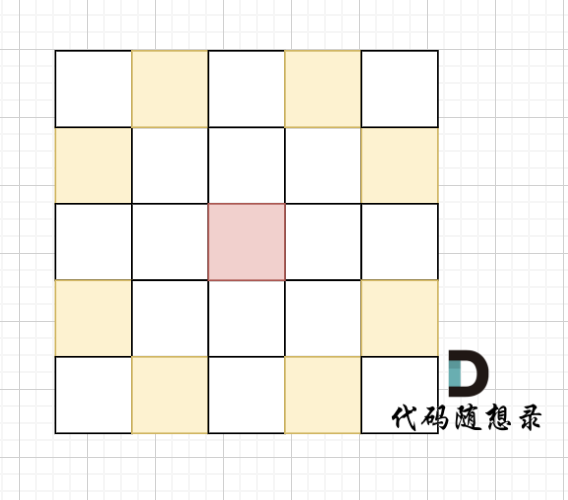
棋盘大小 1000 x 1000(棋盘的 x 和 y 坐标均在 [1, 1000] 区间内,包含边界)
输入描述
第一行包含一个整数 n,表示测试用例的数量。
接下来的 n 行,每行包含四个整数 a1, a2, b1, b2,分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。
输出描述
输出共 n 行,每行输出一个整数,表示骑士从起点到目标点的最短路径长度。
输入示例
6
5 2 5 4
1 1 2 2
1 1 8 8
1 1 8 7
2 1 3 3
4 6 4 6
输出示例
2
4
6
5
1
0
思路:
看到这个题目的第一想法就是广搜:
import java.util.*;
public class Main {
private static int[][] move=new int[1001][1001];
private static int[][] dir = {
{1, -2}, {-1, -2}, {-1, 2}, {1, 2}, {2, -1}, {-2, -1}, {-2, 1}, {2, 1}
};
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
for (int i = 0; i < n; i++) {
int a1 = in.nextInt();
int a2 = in.nextInt();
int b1 = in.nextInt();
int b2 = in.nextInt();
for(int j=0;j<=1000;j++){
for(int k=0;k<=1000;k++){
move[j][k]=0;
}
}
bfs(a1, a2, b1, b2);
System.out.println(move[b1][b2]);
}
}
public static void bfs(int x, int y, int x2, int y2) {
Queue<Integer> q = new LinkedList<>();
q.offer(x);
q.offer(y);
while (!q.isEmpty()) {
int curx=q.poll();
int cury=q.poll();
if(curx==x2&&cury==y2)break;
for (int i = 0; i < 8; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 1 || nexty < 1 || nextx > 1000 || nexty > 1000) continue;
if (move[nextx][nexty]==0) {
move[nextx][nexty] = move[curx][cury] + 1;
q.offer(nextx);
q.offer(nexty);
}
}
}
}
}但是这样写是超时的,因为本题棋盘很大1000*1000,这就可能导致我们有很多点都需要查询。所以我们要考虑怎么不去搜索一些没必要的节点。
我们可以使用优先队列,队列中的元素按照权值F从小到大去排序。
F是什么?
G表示起点到当前遍历节点的路径消耗;
H表示目前遍历节点到最终节点的预估消耗;(注意这里的区别)
F=G+H。
代码如下:
import java.util.*;
class Knight{
int x,y;
// F = G + H
// G = 从起点到该节点路径消耗
// H = 该节点到终点的预估消耗
int f,g,h;
public Knight(int x,int y,int g,int h){
this.x=x;
this.y=y;
this.f=g+h;
this.g=g;
this.h=h;
}
}
class MyComparison implements Comparator<Knight>{
public int compare(Knight k1,Knight k2){
return Integer.compare(k1.f,k2.f);
}
}
public class Main {
private static int[][] move=new int[1001][1001];
private static int[][] dir = {
{1, -2}, {-1, -2}, {-1, 2}, {1, 2}, {2, -1}, {-2, -1}, {-2, 1}, {2, 1}
};
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
for (int i = 0; i < n; i++) {
int a1 = in.nextInt();
int a2 = in.nextInt();
int b1 = in.nextInt();
int b2 = in.nextInt();
for(int j=0;j<=1000;j++){
for(int k=0;k<=1000;k++){
move[j][k]=0;
}
}
bfs(a1, a2, b1, b2);
System.out.println(move[b1][b2]);
}
}
public static void bfs(int x, int y, int x2, int y2) {
PriorityQueue<Knight> q = new PriorityQueue<>(new MyComparison());
int g=0;
int h=(x-x2)*(x-x2)+(y-y2)*(y-y2);
q.offer(new Knight(x,y,g,h));
while (!q.isEmpty()) {
Knight cur=q.poll();
if(cur.x==x2&&cur.y==y2)break;
for (int i = 0; i < 8; i++) {
int nextx = cur.x + dir[i][0];
int nexty = cur.y + dir[i][1];
if (nextx < 1 || nexty < 1 || nextx > 1000 || nexty > 1000) continue;
g=cur.g+5;
h=(nextx-x2)*(nextx-x2)+(nexty-y2)*(nexty-y2);
if (move[nextx][nexty]==0) {
move[nextx][nexty] = move[cur.x][cur.y] + 1;
q.offer(new Knight(nextx,nexty,g,h));
}
}
}
}
}
时间复杂度:
最坏情况:O(n*2),n是节点数量
最佳情况:从起点直接到终点,O(dlogd)(d表示起点到终点的深度)