一、训练速度慢——更快的优化器
训练一个非常大的深度神经网络可能会非常缓慢。
目前接触过4种加快训练速度的方法:对连接权重应用良好的初始化策略,使用良好的激活函数,使用批量归一化,以及重用建立在辅助任务或无监督学习获得的预训练网络。
现在提出另一种加速训练的方式,对梯度下降做改进:优化器。将介绍流行的优化算法:动量优化,Nesterov加速梯度,AdaGrad,RMSProp,以及Adam及其变体
1、动量优化——SGD中的参数
其核心思想来自物理中的动量:想象一个球从斜坡上滚下,刚开始速度很慢,但速度会越来越快,直到达到最终速度(假设有摩擦力+空气阻力,速度不能无限增长),这就是动量优化背后的核心思想。
常规梯度下降法会在坡度平缓时采取小步,而在坡度大时采取大步,但永远不会关心之前的梯度是什么,永远不会加快速度,如果局部梯度很小,则它会下降得非常缓慢。
动量优化把梯度看成力的方向/加速度的方向,会累积之前的梯度:在每次迭代时,都会从动量向量(速度)m 减去 学习率乘以局部梯度(加速度),并通过加上该动量来更新权重。
为了模拟摩擦力,防止动量(速度)变得过大,该算法引入了一个新的超参数β,0代表高摩擦,退化为之前的梯度下降,1表示没有摩擦,β会设置为0-1之间的某个值,典型的β值是0.9。
动量优化公式:
可以轻松验证,如果梯度保持恒定,则最终速度(即权重更新的最大大小)等于该梯度乘以学习率 再乘以
(忽略符号)。例如,如果
,则最终速度等于梯度乘以学习率的10倍,因此动量优化最终比梯度下降快10倍!这使动量优化比梯度下降要更快地从"平台"逃脱。
在讨论线性回归的梯度下降时,当输入的尺寸差别非常巨大,代价函数将看起来像一个拉长的碗。梯度下降相当快地沿着陡峭的"斜坡"下降,但是沿着"山谷"下降需要很长时间。相反,动量优化将沿着"山谷"滚动得越来越快,直到达到"谷底"(最优解)。在不使用批量归一化的深度神经网络中,上面的层通常会得到尺寸差别较大的输入,因此使用动量优化可以在梯度方向改变频繁的维度上抑制震荡,使路径更加平滑,从而更快受凉并绕过局部优化问题。
# 在Keras中实现动量优化:只需要使用SGD优化器并设置其momentum超参数即可
optimizer_momentum = tf.keras.optimizers.SGD(learning_rate=0.001, momentum=0.9)
动量值取0.9通常在实践中效果很好,几乎总是比常规的梯度下降法更快。有时也会用到0.99,表示保留更多的历史动量,加速效果更强,但是可能需要更小的学习率。
2、Nesterov加速梯度——SGD中的参数
动量优化公式:
它是动量优化的一个小变体,会比常规动量优化快。Nesterov加速梯度(NAG)方法也称为Nesterov动量优化,它不是在局部位置 ,而是在动量方向稍前方
处测量代价函数的梯度。 这种小的调整之所以有效是因为通常动量向量会指向正确的方向(即朝向最优值),因此使用在该方向上更远处而不是原始位置测得的梯度会稍微准确一些。
如下图所示(其中 代表在起点
处测量的代价函数的梯度,
代表
点的梯度)。
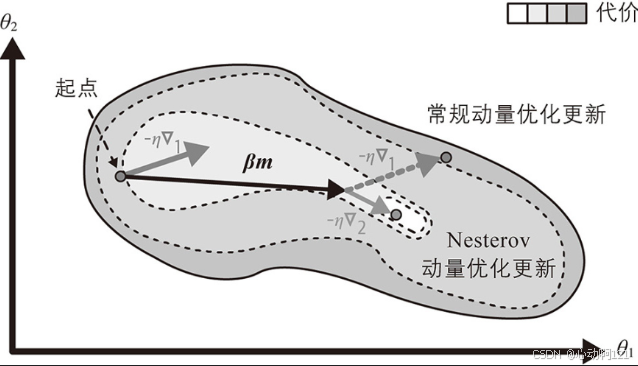
Nesterov动量优化更新最终稍微接近最优解。一段时间后,这些小的改进累积起来,NAG就比常规的动量优化要快得多。此外,请注意,当动量势头推动权重跨越谷底时,∇1继续推动越过谷底,而∇2则推回谷底。这有助于减少振荡,因此NAG收敛速度更快。
# 要使用NAG,只需在创建SGD优化器时设置nesterov=True即可
optimizer_nesterov = tf.keras.optimizers.SGD(learning_rate=0.001, momentum=0.9, nesterov=True)更加直观的比喻,想象一个球从山上滚下来:
标准梯度下降:球只看自己脚下的坡度来决定往哪里滚。
动量法:球有一个速度。它根据脚下的坡度和当前速度来决定滚动。但因为它只看脚下,快到谷底时可能会因为速度太快而冲过谷底。
NAG:这是一个“聪明”的球。它先根据自己当前的速度预测一下自己下一秒会在什么位置,然后它提前看了一眼那个预测位置的坡度。如果预测位置的坡度已经向上(说明前面是谷底另一边),它就会提前减速;如果预测位置坡度依然向下,它就会放心地加速。这使得它的行为更加“未雨绸缪”。
3、AdaGrad算法——Adagrad优化器
AdaGrad(自适应梯度)算法的核心思想是:为模型中的每个参数自适应地调整学习率,也就是根据参数地历史梯度平方和来调整当前参数地学习率。这种自适应能力使其特别适合处理稀疏数据(即很多特征出现次数很少的数据)。
- 对于频繁更新(梯度大)的参数:它的学习率会变得较小,因为其历史梯度平方和较大。这使得参数的更新步伐更稳健,避免震荡。
- 对于不频繁更新(梯度小)的参数:它的学习率会变得相对较大,因为其历史梯度平方和较小。这使得参数的更新步伐更大,加速学习。
每次迭代的更新规则:
- 计算当前批次的梯度:
- 累计历史梯度的平方:
,
表示按元素相乘
- 计算参数更新量:
,
表示学习率因子
- 更新参数:
optimizer_adagrad = tf.keras.optimizers.Adagrad(learning_rate=0.001)4、RMSProp算法(AdaGrad的改进)——SMSProp优化器
RMSProp(Root Mean Square Propagation,均方根传播)完全是为了解决 AdaGrad 学习率过早衰减 的问题而设计的。
该算法的核心思想是:不再无脑地累加全部历史梯度平方,而是引入一个衰减率,让很久之前的梯度贡献逐渐减小,从而专注于最近一段时间的梯度规模。 这样,累积值 就不会无限增大,学习率也就不会最终降为零。
每次迭代的更新规则:
- 计算当前批次的梯度:
- 累计历史梯度的平方:
,
表示按元素相乘,
是衰减率(动量),通常设置为0.9或0.99
- 计算参数更新量:
,
表示学习率因子
- 更新参数:
optimizer_rmsprop = tf.keras.optimizers.RMSprop(learning_rate=0.001, rho=0.9)| 优点 | 缺点 |
|---|---|
| 解决AdaGrad的致命缺陷:学习率不会单调下降至零,使得模型在训练后期也能有效学习 | 引入一个新的超参数衰减率 不过这个参数通常很稳定,设置为0.9、0.99在大多数情况下都能很好的工作 |
| 继承了AdaGrad的优点:仍然为每个参数自适应调整学习率,在非平稳目标和稀疏梯度上表现良好 | 学习率的调整仍然依赖于历史的梯度平方,这意味着符号信息被丢失了(正负梯度一样对待),导致调整可能不够精确 |
5、Adam算法(动量+RMSProp)—— Adam优化器
结合了上边两种优化算法思想:动量和RMSProp。像动量优化一样,跟踪过去梯度的指数衰减平均值,就像RMSProp一样,它跟踪过去平方梯度的指数衰减平均值,相当于对梯度的均值和方差(不减平均值)估计。
初始化的时候 都是初始化为0,之后的更新规则:
,
表示时间步计数器
- 计算当前小批量梯度:
- 更新有偏一阶矩阵估计(动量):
,
就是动量优化中的
,
是一阶矩阵向量(类似动量中的速度变量)
- 更新有偏二阶矩阵估计(梯度平方):
,
是RMSProp中的
,
是二阶矩阵向量(存储梯度平方的移动平均)。这里如果突然出现一个巨大梯度,那么
会因为这个巨大梯度而瞬间飙升,但又可能因为后续的小梯度而快速下降。
- 计算一阶矩的偏差矫正:
- 计算二阶矩的偏差矫正:
- 更新参数:
学习率(Learning Rate):这是最重要的超参数,通常需要尝试设置,如0.001, 0.0003等。Adam对初始学习率不那么敏感,但仍然需要设置。由于Adam是一种自适应学习率算法,像AdaGrad和RMSProp一样,因此几乎很少需要对学习率超参数进行调整。通常可以使用默认值0.001,这使得Adam甚至比梯度下降更易于使用。
:一阶矩的衰减率,通常设置为 0.9。控制动量部分的记忆程度。