目录
目标:设计一个BP网络,逼近非线性函数
代码:先画出要逼近的函数,再用没有训练的神经网络去逼近
clear all
clc
k=2;
p=[-1:0.05:9];
t=1+sin(k*pi/2*p);
%%%%开始建立一个网络结构%%%%
n=5;
net=newff(minmax(p),[n,1],{'tansig','purelin'},'trainlm');
y1=sim(net,p);%用sim 观察网络的输出
figure;
plot(p,t,'-',p,y1,':');
title('没有训练的输出结果');
xlabel('时间');
ylabel('仿真输出--原函数--');观察效果,逼近的效果不好

用训练过的神经网络逼近非线性函数
clear all
clc
k=2;
p=[-1:0.05:9];
t=1+sin(k*pi/2*p);
%%%%开始建立一个网络结构%%%%
n=3;
net=newff(minmax(p),[n,1],{'tansig','purelin'},'trainlm');
y1=sim(net,p);%用sim 观察网络的输出
%%%先训练网络,再仿真%%%
net.trainParam.epochs=200;
net.trainParam.goal=0.2;
net=train(net,p,t);
y2=sim(net,p);
figure;
plot(p,t,'-',p,y1,':',p,y2,'--');
title('训练的输出结果');
xlabel('时间');
ylabel('仿真输出');':' 是没有训练的, '--' 是训练过的

训练过的神经网络逼近效果明显好于未训练的。
下一步:增大n值(神经网络隐藏层的数量)
n=5时:
clear all
clc
k=2;
p=[-1:0.05:9];
t=1+sin(k*pi/2*p);
%%%%开始建立一个网络结构%%%%
n=5;
net=newff(minmax(p),[n,1],{'tansig','purelin'},'trainlm');
y1=sim(net,p);%用sim 观察网络的输出
%%%先训练网络,再仿真%%%
net.trainParam.epochs=200;
net.trainParam.goal=0.2;
net=train(net,p,t);
y2=sim(net,p);
figure;
plot(p,t,'-',p,y1,':',p,y2,'--');
title('训练的输出结果');
xlabel('时间');
ylabel('仿真输出');
逼近效果好于n=3

n=20
clear all
clc
k=2;
p=[-1:0.05:9];
t=1+sin(k*pi/2*p);
%%%%开始建立一个网络结构%%%%
n=20;
net=newff(minmax(p),[n,1],{'tansig','purelin'},'trainlm');
y1=sim(net,p);%用sim 观察网络的输出
%%%先训练网络,再仿真%%%
net.trainParam.epochs=200;
net.trainParam.goal=0.2;
net=train(net,p,t);
y2=sim(net,p);
figure;
plot(p,t,'-',p,y1,':',p,y2,'--');
title('训练的输出结果');
xlabel('时间');
ylabel('仿真输出');
说明增大n(隐藏层的数量),可以增加BP神经网络预测的准确值。
下面改变频率参数k:
k=2,n=3 和 k=2,n=10
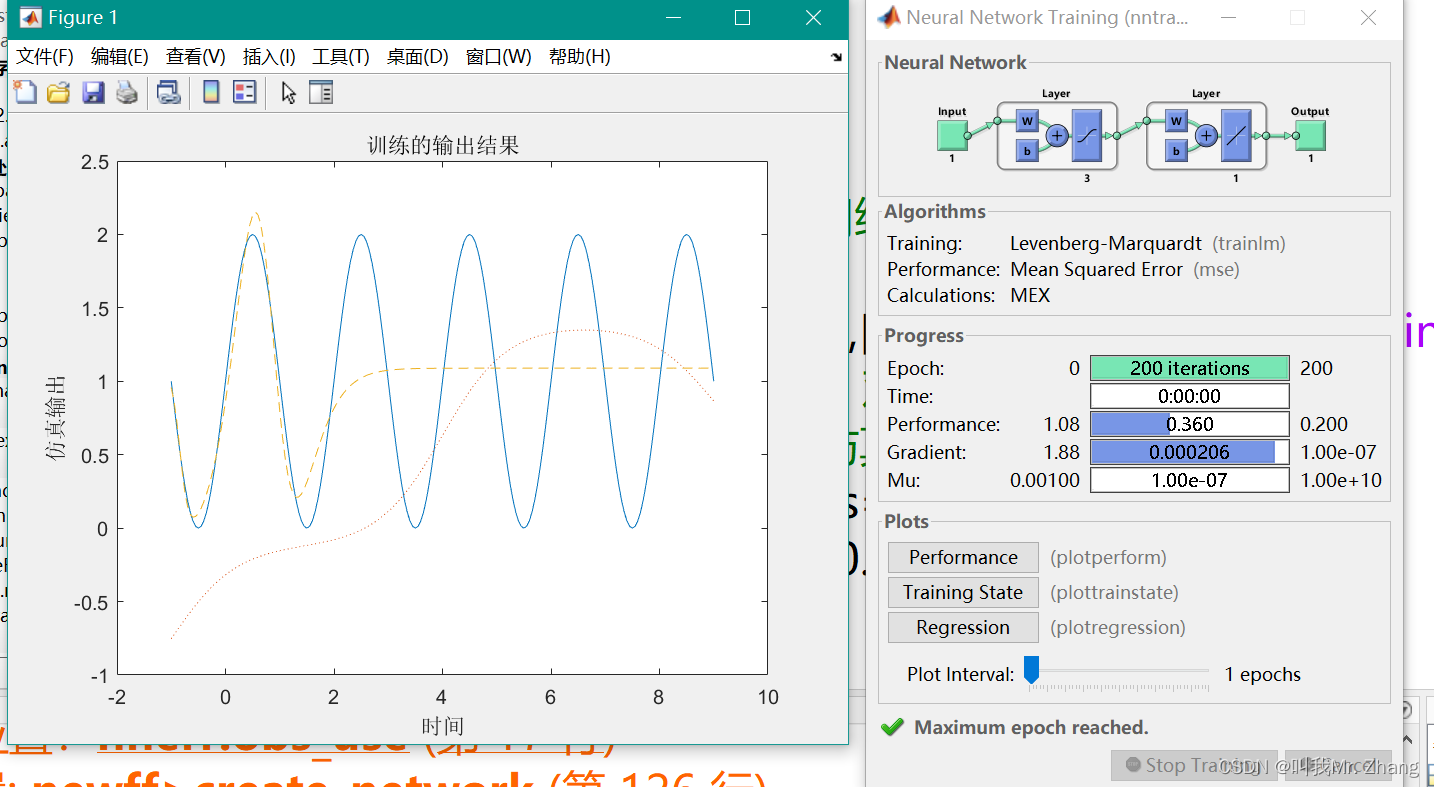
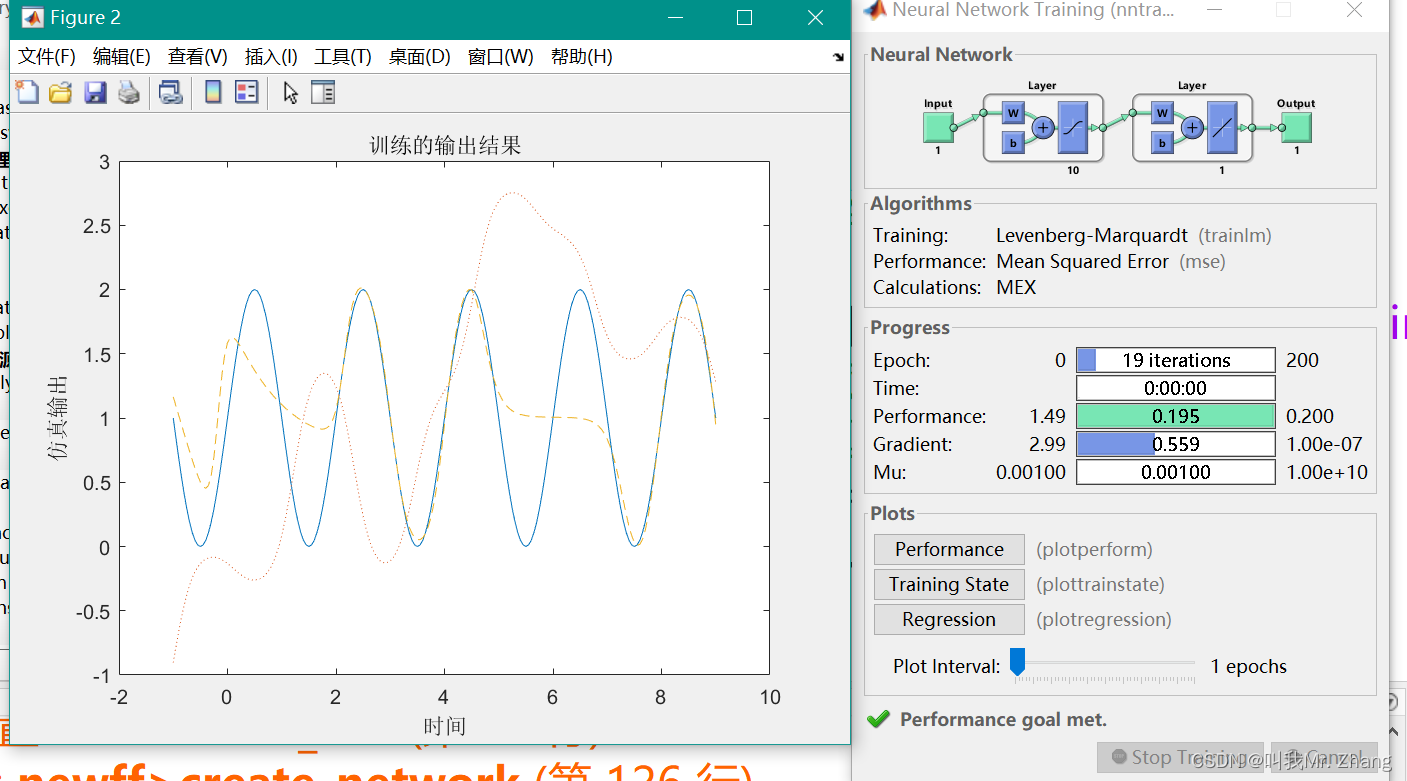
k=3,n=3 和 k=3,n=10
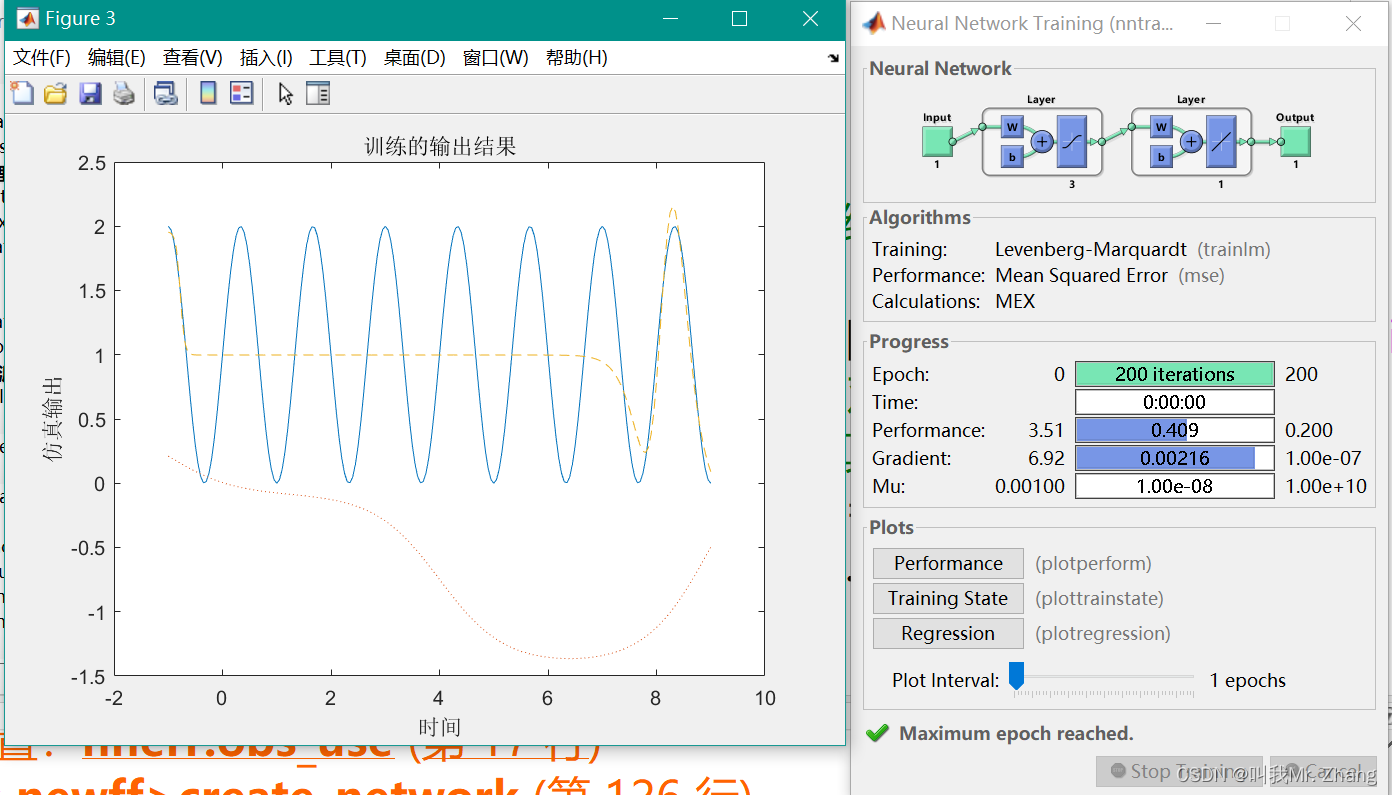
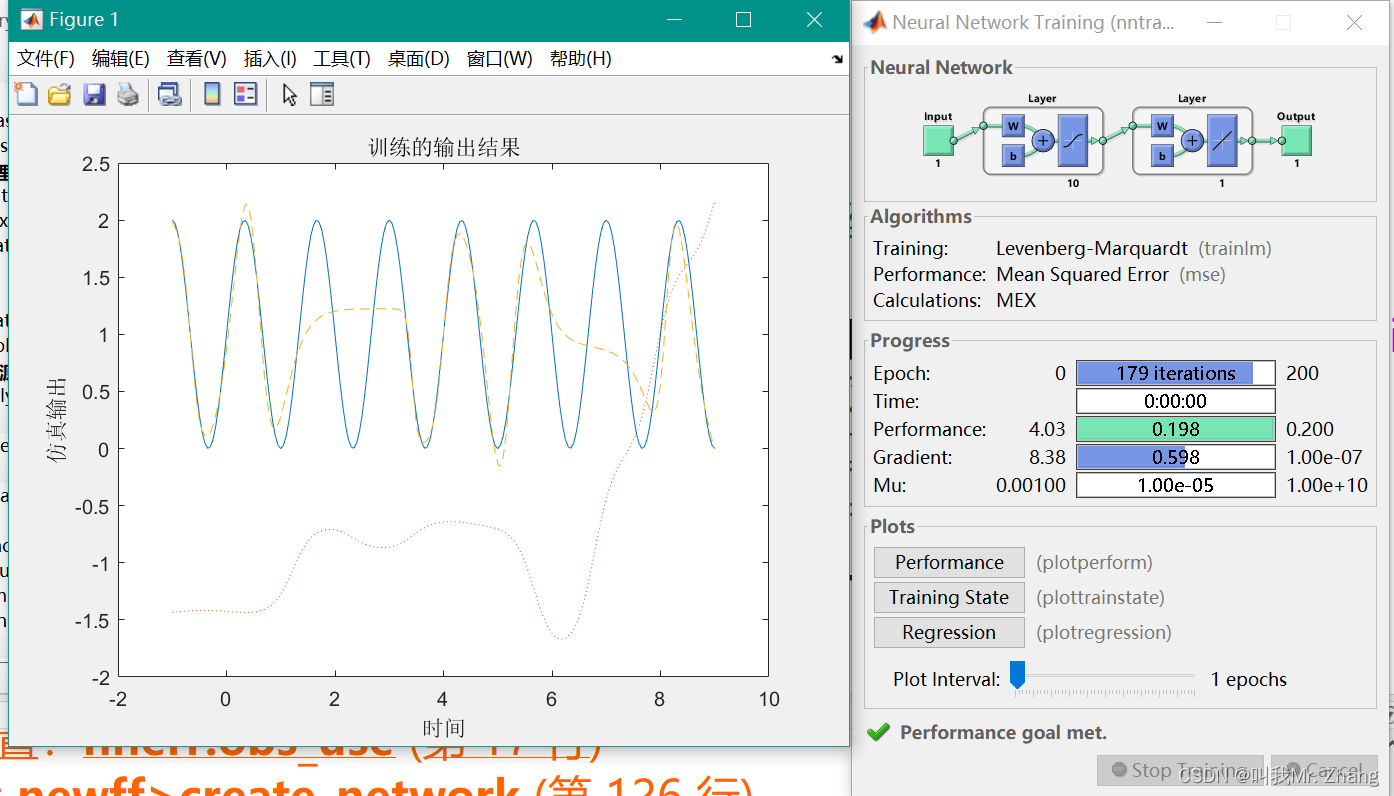
k=6,n=3 和 k=6,n=10

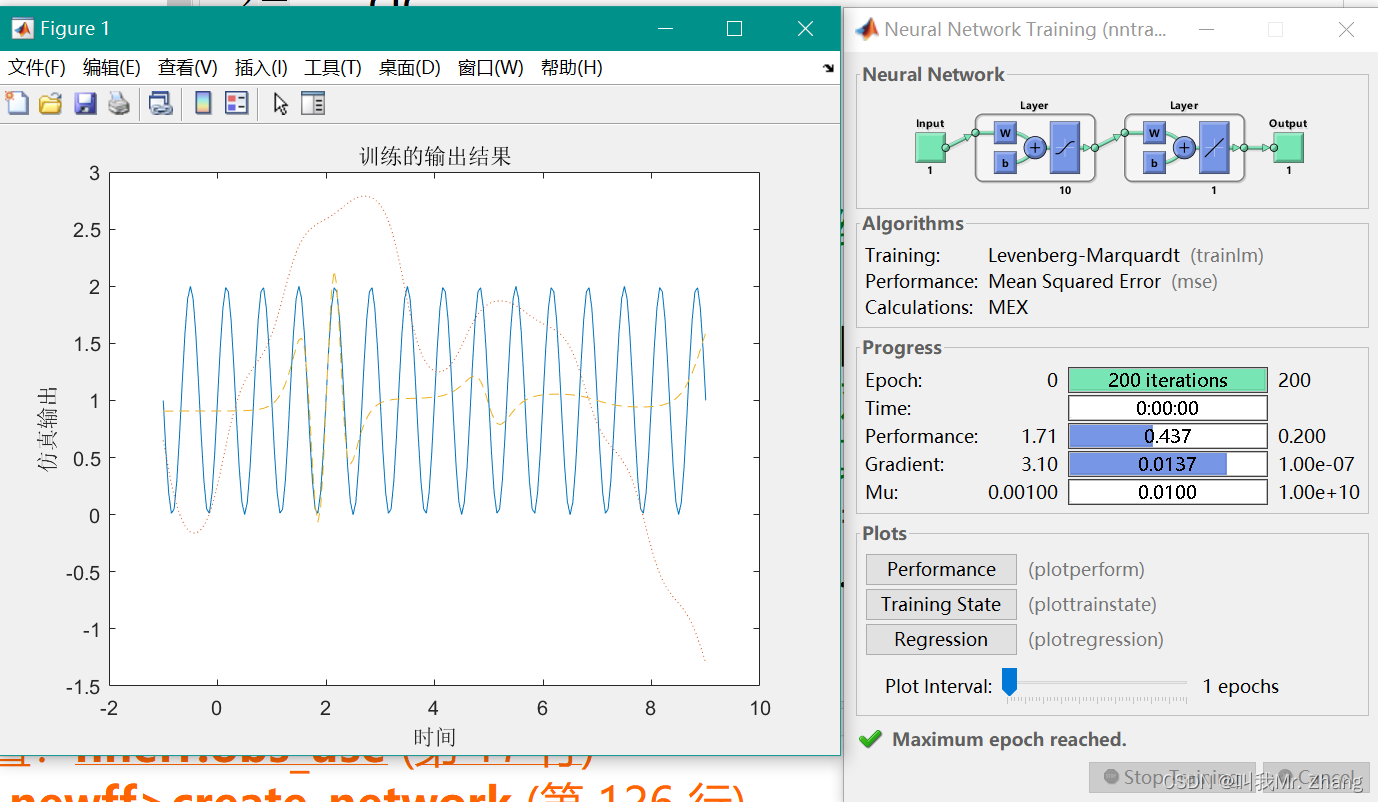 说明不同频率下均存在,增大隐藏层,增大BP神经网络的逼近效果。
说明不同频率下均存在,增大隐藏层,增大BP神经网络的逼近效果。
本文含有隐藏内容,请 开通VIP 后查看