math_函数图像的变换&坐标系平移变换&奇偶函数之间组合与复合后的奇偶性/周期函数的性质

坐标系平移

这部分内容是本人主观看法

• 正确性有待验证

• $设坐标系C_0上有一点p_0^0(m,n)$

• $坐标系C_1上有一点p_0^1(0,0);该点是由p_0^0经过相应的平移映射而来$

• $$\begin{gathered} 即,假设平移规则为:c_0坐标的原点移动到c_0的(m,n)位置, \\ 以该位置作为新坐标系c_1的坐标原点(0,0{)}_{c_1} \end{gathered}$$

  • $$\begin{gathered} (m,n{)}_{c_0}\to (0,0{)}_{c_1} \\ 则(0,0{)}_{c_0}\to (-m,-n{)}_{c1} \\ 则(x,y{)}_{c_0}\to (x-m,y-n{)}_{c1} \end{gathered}$$

  • $$\begin{gathered} 记c_0坐标上的点为(x_0,y_0) \\ {c}_1坐标上点为(x_1,y_1) \\ \{\begin{array}{l}{x}_1=X(x_0)=x_0-m\\ y_1=Y(y_0)=y_0-n\end{array} \end{gathered}$$

  • $$\begin{gathered} 对于c_0上的曲线方程B_0:\frac{x_0^2}{a}+\frac{y_0^2}{b}=1 \\ 对于c_1上的曲线方程B_1:\frac{x_1^2}{a}+\frac{y_1^2}{b}=1 \\ 由上述映射关系(参数方程) \\ {B}_1在c_0上的方程为:\frac{(x_0-m{)}^2}{a}+\frac{(y_0-n{)}^2}{b}=1 \end{gathered}$$

  • $$\begin{gathered} 同理,可以得到B_0在c_1坐标系上的方程为:\frac{(x_0+m{)}^2}{a}+\frac{(y_0+n{)}^2}{b}=1 \\ 还比如,可以用容易验证的圆方程R:x_1^2+y_1^2=r^2(C_1上) \\ (x_0-m{)}^2+(y_0-n{)}^2=r^2(c_0坐标系投影到C_0上) \end{gathered}$$

  • 更一般的,有
    $$\begin{gathered} c_1坐标系(层)上的曲线B(x_1,y_1)=0 \\ 在c_0坐标系上可以这样描述B(x_0-m,y_0-n)=0 \end{gathered}$$

$$

$$

函数的左右平移

• 中学的时候,有句关于函数平移的话:

  • 我们记平移前的函数为f(x),平移后的函数为g(x)

    平移的距离记为d

    $$f(x)\stackrel{平移操作(距离为d)}{\Rightarrow }g(x)$$

  • 左加右减

    • $f(x)向左平移,g(x)=f(x+d)$
    • $f(x)向右平移,g(x)=f(x-d)$

  • 上加下减

    • $f(x)向上平移,g(x)=f(x)+d$
    • $f(x)向下平移,g(x)=f(x)-d$

  • 

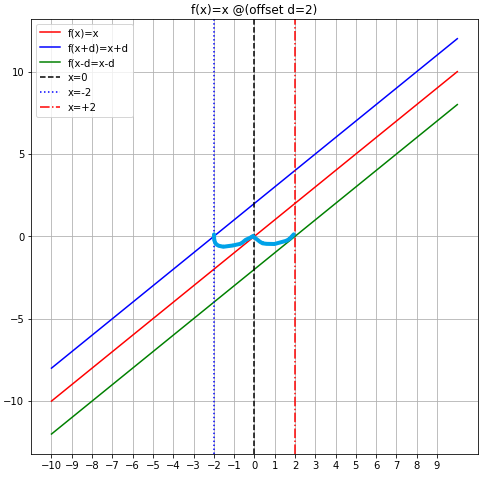
  • 函数图像平移可以理解为,函数图像上的所有点沿着同一个方向平移相同的距离

  • 假设这个距离为d

对于右平移

从代数坐标角度来看

• 取图像上的任意一点$A(x_0,f(x_0))$,经过平移后的点$B(x_1,g(x_1))$

  • $$\begin{gathered} x_1=x_0+d \\ 则坐标:B(x_1,g(x_1))=(x_0+d,g(x_0+d)) \end{gathered}$$

  • 又因为仅仅是水平平移(左/右平移是水平平移),平移前后两个点的纵坐标保持相等

    • $$\begin{gathered} f(x_0)=g(x_1)=g(x_0+d) \\ 即g(x_0+d)=f(x_0) \end{gathered}$$

  • 这个过程,不失一般性,则

    $$g(x+d)=f(x)$$

​

• 下面对该式$g(x+d)=f(x)$进行变形

  • 配凑法

    • $$\begin{gathered} 令h(x)=x-d \\ 取x=h(x)带入到g(x+d)=f(x),得到g(x-d+d)=f(x-d),从而: \\ g(x)=f(x-d) \end{gathered}$$

  • 换元法

    • $$\begin{gathered} 不妨令t=x+d,则 \\ x=t-d \end{gathered}$$

    • 将t,x分别替换

    • $$g(t)=f(t-d)$$

    • 我们将自变量t改写为x,

    • 则
      $$g(x)=f(x-d)$$

• 这就是右减的含义

整理:从图像的角度(图像点坐标回退/前进)

图像的角度,更确切的说,是图像上的点的平移的角度来看

• f(x)图像向右平移距离d,得到的图像是函数g(x)的图像

• $g(x)在x=x_0处的坐标A^{\prime }(x_0,g(x_0))与平移之前的该点本应该处在的位置坐标:A(x_0-d,f(x_0-d))满足如下关系:$

  • $A^{\prime }和A的纵坐标相等$,即
    $$g(x_0)=f(x_0-d)$$

• 该条件是不失一般性的,所以,可以用一般性的x代替具体的$x_0$,从而:

• $$g(x)=f(x-d)$$

左平移

• 类似右平移的分析

翻折变换(对称变换😀)

$f(-x)\&f(x)关于y轴对称$

• 我们像研究其他图像在坐标系上的变换那样,研究点来间接研究线(图像变换)

$$\begin{gathered} 在x=a处的 \\ 可以取函数f(x)上的点A(a,f(a)) \\ 对于f(-x),点B(-a,f(a)) \\ 由于a的一般性(任意性),所以对定义域内所有x对应的点(x,f(x))和(x,f(-x))关于y轴对称 \\ 所以f(-x)和f(x)关于y轴对称 \end{gathered}$$

The graph of $f(-x)$ is the mirror image of the graph of $f(x)$ with respect to the vertical axis.
The graph of $-f(x)$ is the mirror image of the graph of $f(x)$ with respect to the horizontal axis.

A function is called even if $f(-x)=f(x)$ for all x (For example, cos(x)).
A function is called odd if $f(-x)=-f(x)$ for all x (For example, sin(x)).

$-f(x)\&f(x)关于x轴对称$

和上面的分析类似,取点分析
$$\begin{gathered} A(a,f(a))和B(a,-f(a)) \\ 显然两点关于x周对称,故而可以知道-f(x)和f(x)关于x轴对称 \end{gathered}$$

$关于x=u对称$

• $如果f(x)关于x=u对称$

  • $定义域自然也得关于x=u对称$

  • $如果f(x_1)=f(x_2),x_1+x_2=2u$

    • $f(x_1)=f(2u-x_1)$
    • 即$f(x)=f(2u-x)$

  • 例如$y(x)=(x-1{)}^2;y(2-x)=((2-x)-1{)}^2=(1-x{)}^2=(x-1{)}^2$

    • $y(x)=y(2-x),对称轴为u=\frac{1}{2}\cdot 2=1$

    • $特别的,偶函数关于x=0对称$

      • $f(x)=f(-x),对称轴x=u=0:x+(-x)=2u=0;u=0$

奇偶性

推导方法

• 均可以通过奇偶函数的定义来直白推导

函数记号声明

• 设函数

  • $O(x)为奇函数(odd(x));$

    • $o(-x)=-o(x)$
      • $o_i(x);o_j(x)表式任意两个偶函数$

  • $E(x)为偶函数(even(x))$;

    • $e(-x)=e(x)$
      • $e_i(x);e_j(x)表式任意两个奇函数$

和差

• $设h_1(x)=o_1(x)+o_2(x)$
  • $h_1(-x)=o_1(-x)+o_2(-x)=-o_1(x)-o_2(x)=-(o_1(x)+o_2(x))=-h_1(x)$
  • $若设h_1(x)=o_1(x)-o_2(x)$
    • $h_1(-x)=o_1(-x)-o_2(-x)=-o_1(x)+o_2(x)=-h_1(x)$
  • 可见,奇函数相加减,得到的新函数还是奇函数
• $h_2(x)=e_1(x)\pm e_2(x)$
  • $h_2(-x)=e_1(-x)\pm e_2(-x)=(e_1(x)\pm (e_2(x))=h_2(x)$
  • $可见h_2是奇函数,偶函数相加减得到的新函数仍为偶函数$
• 奇函数$\pm$偶函数的结果没有一般性的定论

乘积

• $h_1(x)=o(x)e(x)$
  • $h_1(-x)=o(-x)e(-x)=-o(x)e(x)=-h_1(x)$
  • $可见h_1是奇函数$
• $h_2(x)=o_1(x)o_2(x)$
  • $h_2(-x)=o_1(-x)o_2(-x)=(-o_1(x))(-o_2(x))=o_1(x)o_2(x)=h_2(x)$
  • $可见h_2是偶函数$
• $h_3(x)=e_1(x)e_2(x)$
  • $h_3(-x)=e_1(-x)e_2(-x)=e_1(x)e_2(x)=h_3(x)$
  • $可见h_3是偶函数$

商

• 推导方法类似于乘积部分
• $y(x)=\frac{f(x)}{g(x)}$
• $y(-x)=\frac{f(-x)}{g(-x)}$
• $利用f(x)和g(x)的奇偶性,将y(-x)表示为\pm \frac{f(x)}{g(x)}(即\pm y(x))$
• 或者利用复合性结论,转化为乘法
  • $y(x)=\frac{o(x)}{e(x)}=o(x)\cdot \frac{1}{e(x)}$

奇偶函数间复合函数的奇偶性

• $y=f(u);u=g(x)$
  • $y(x)=f_g(x)=f(g(x))的奇偶性$
    • $例如,f(u)=\frac{1}{u};u=g(x)=x^2$
    • $显然f(u)是个奇函数(反比例函数);g(x)是偶函数$
    • $y(x)=\frac{1}{x^2}则是偶函数$

讨论具体情况:

• 为了便于提高推导效率,$沿用前面的o(x),e(x)的含义$

$y_1(x)=o(e(x))$

• $y(-x)=o(e(-x))=o(e(x))=y(x)$
• $可见y_1(x)是偶函数$
• 特例助记:$y(u)=u;u=x^2;y(x)=x^2(偶函数)$

$y_2(x)=o_1(o_2(x))$

• $$y_2(-x)=o_1(o_2(-x))=o_1(-o_2(x))=-o_1(o_2(x))=-y_2(x)$$

$y_3(x)=e_1(e_2(x))$

• $y_3(-x)=e_1(e_2(-x))=e_1(e_2(x))=y_3(x)$
  • $其中,记u=e_2(x);e_1(-e_2(x))=e_1(-u)=e_1(u)=e_1(e_2(x))$

$y_4(x)=e(o(x))$

• $y_4(-x)=e(o(-x))=e(-o(x))=e(o(x))=y_4(x)$

奇偶性小结

和差小结

• $奇函数\pm 奇函数=奇函数$
• $偶函数\pm 偶函数=偶函数$
• $奇函数\pm 偶函数(没有通用定论)$

乘积和商小结

• 乘法和除法运算得到的新函数的奇偶性判定方式十分一致
  • 奇偶性相同的函数乘积或商的奇偶性是偶函数
  • 奇偶性不同的函数乘积或商的奇偶性是奇函数
  • 类似与异或运算

奇偶函数复合小结

• 仅在奇函数相互复合的情况下才得到奇函数
• 而对于奇偶函数复合的其他情况中,复合函数中无论是外层还是内层,只要由一个是偶函数,那么复合结果就是偶函数
• 类似于复合与运算

推广

• 利用类似的推导方式
• 或者反复使用上述已经得到的结论,可以得到
  • $y(x)=\prod _{i=1}^n{f}_i(x)的奇偶性$
  • …

定义域对称于原点的函数与奇偶函数间的关系

$对于定义在对称于原点的数集X上的函数f(x),可以分解为一个奇函数+偶函数之和$

倍乘非零常数不改变奇偶性

• $设k为非零常数,t(x)=kf(x);t(-x)=kf(-x),容易通过奇偶性定义验证,t(x)的奇偶性和f(x)一致;$

  • 可见,$对f(x)乘以一个常数k(k\ne 0),新函数的奇偶性与f(x)奇偶性一致$

• $h(x)=f(x)-f(-x)$

  • $h(-x)=f(-x)-f(x)=-h(x)$
  • $h(x)(以及k\cdot h(x)都是奇函数;$

• $g(x)=f(x)+f(-x)$

  • $g(-x)=f(-x)+f(x)=g(x)$
  • $g(x)(以及k\cdot g(x)都是偶函数;$

• $由于f(x)=\frac{1}{2}h(x)+\frac{1}{2}g(x),所以结论正确$

周期性

• $设f(x+t_0)=f(x),则f(x)是以t_0为周期的周期函数$

• $$\begin{gathered} 设y(x)=f(u(x)),则y(x+t_1)=f(u(x+t_1)) \\ 若y(x+t_1)=y(x),那么y(x)就是以t_1为周期的周期函数 \\ ★并且,约定t_0和t_1分别是f(x)和y(x)的最小正周期(如果存在的话)★ \\ 设f(x)上有一点A(p,f(a)),B(p+t_0,f(p+t_0)=f(p)) \\ y(x)上有一点M(p,y(p)),N(p+t_1,y(p+t_1)) \\ 设u(x)=ax+b \\ \{\begin{array}{l}y(p)=f(ap+b);\\ y(p+t_1)=f(a(p+t_1)+b)=f(ap+a{t}_1+b)=f(ap+b+a{t}_1)\end{array} \\ 记u_0=ap+b \\ 另一方面,由于设定的周期函数f的特点:f(u_0+t_0)=f(u_0) \\ 根据周期函数的定义(性质),可以比较花括号两个等式的右侧, \\ 可以看出t_0和t_1间的联系:n\times t_0=a\cdot t_1,(n\in \mathbb{Z}) \\ 即对于f(u)(或者说f(x)也一样)来说,a{t}_1是f(x)的最小正周期t_0的整数倍 \\ 由于我们取t_1是最小正周期所以:t_1=\frac{n{t}_0}{a};an取其最小绝对值|a|,(n=1) \\ 则t_1=\frac{t_0}{|a|} \end{gathered}$$

  上述结论在三角函数上用的很多,$例如sin\omega x的周期是sinx周期t_0=2\pi 的\frac{1}{|\omega |}倍:即\frac{2\pi }{|\omega |};sin(3x)的周期为\frac{2\pi }{3}$

周期函数间的组合

不同周期函数值和构成的新函数的周期?

• 明白这一点很重要,在傅里叶级数中,会用到这一点

• 不同周期函数 t i ( x ) 的和函数 s ( x ) = ∑ i = 1 n t i 的周期是这些周期 t i ( x ) 周期的最小公倍数 l c m ( { t i } ) 不同周期函数t_i(x)的和函数s(x)=\sum\limits_{i=1}^{n}t_i的周期是这些周期t_i(x)周期的最小公倍数lcm(\{t_i\}) 不同周期函数ti​(x)的和函数s(x)=i=1∑n​ti​的周期是这些周期ti​(x)周期的最小公倍数lcm({ti​})

• f ( x + t 0 ) = f ( x ) g ( x + t 1 ) = g ( x ) 记 h ( x ) = f ( x ) + g ( x ) ; l c m = k 0 t 0 = k 1 t 1 更一般的 , 我们记小周期函数 t i ( x ) 的最小公倍数 : l c m = l c m { t i } = k i t i , ( i = 1 , 2 , 3 , . . . ) ; ( l c m { t i } = k 0 t 0 = k 1 t 1 = . . . ) h ( x + l c m ) = f ( x + l c m ) + g ( x + l c m ) = f ( x + k i 0 t 0 ) + g ( x + k i 1 t 1 ) = 周期函数的性质 f ( x ) + g ( x ) 更一般的 s ( x ) = ∑ k = 1 n f k ( x ) 则 s ( x + l c m ) = ∑ k = 1 n f k ( x ) = s ( x ) f(x+t_0)=f(x) \\ g(x+t_1)=g(x) \\记h(x)=f(x)+g(x); \\lcm=k_0t_0=k_1t_1 \\更一般的,我们记小周期函数t_i(x)的最小公倍数: \\lcm=lcm{\{t_i\}}=k_it_i,(i=1,2,3,...); \\(lcm{\{t_i\}}=k_0t_0=k_1t_1=...) \\h(x+lcm)=f(x+lcm)+g(x+lcm) \\=f(x+k_{i_0}t_0)+g(x+k_{i_1}t_1)\xlongequal{周期函数的性质} f(x)+g(x) \\更一般的s(x)=\sum\limits_{k=1}^{n}f_k(x) \\则s(x+lcm)=\sum\limits_{k=1}^{n}f_k(x)=s(x) f(x+t0​)=f(x)g(x+t1​)=g(x)记h(x)=f(x)+g(x);lcm=k0​t0​=k1​t1​更一般的,我们记小周期函数ti​(x)的最小公倍数:lcm=lcm{ti​}=ki​ti​,(i=1,2,3,...);(lcm{ti​}=k0​t0​=k1​t1​=...)h(x+lcm)=f(x+lcm)+g(x+lcm)=f(x+ki0​​t0​)+g(x+ki1​​t1​)周期函数的性质 f(x)+g(x)更一般的s(x)=k=1∑n​fk​(x)则s(x+lcm)=k=1∑n​fk​(x)=s(x)

• $$\begin{gathered} y(x)=f(x)+c \\ y(x+t)=f(x+t)+c=f(x)+c \\ 可见,y(x+t)=y(x),周期函数加上一个常数得到的新函数周期和f(x)一致 \\ 容易验证,乘以一个非零常数有类似的规律: \\ y(x)=kf(x) \\ y(x+t)=kf(x+t)=kf(x) \end{gathered}$$

• 对于

  • 设 s ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s ( n x ) + b n s i n ( n x ) ) 该和函数的各个周周期函数的周期的最小公倍数为 2 π 这些函数的周期分别是 { 2 π n } = 2 π 1 , 2 π 2 , 2 π 3 , . . . 事实上 , 2 π ( 2 π n ) = n , 而 n = 1 , 2 , 3 , . . . 可见 , 2 π 就是他们的最小公倍数 因此 : s ( x + 2 π ) = s ( x ) 设s(x)=\frac{a_0}{2}+\sum\limits_{n=1}^{\infin}(a_ncos(nx)+b_nsin(nx)) \\该和函数的各个周周期函数的周期的最小公倍数为2\pi \\这些函数的周期分别是\{\frac{2\pi}{n}\}=\frac{2\pi}{1},\frac{2\pi}{2},\frac{2\pi}{3},... \\事实上,\frac{2\pi}{(\frac{2\pi}{n})}=n,而n=1,2,3,... \\可见,2\pi就是他们的最小公倍数 \\因此:s(x+2\pi)=s(x) 设s(x)=2a0​​+n=1∑∞​(an​cos(nx)+bn​sin(nx))该和函数的各个周周期函数的周期的最小公倍数为2π这些函数的周期分别是{n2π​}=12π​,22π​,32π​,...事实上,(n2π​)2π​=n,而n=1,2,3,...可见,2π就是他们的最小公倍数因此:s(x+2π)=s(x)