高数——必背秘籍

一、等价无穷小

当x—>0，有：

(1)

• $x\sim sinx\sim tanx\sim arcsinx\sim arctanx\sim ln(x+1)\sim ln(x+\sqrt{1+x^2})\sim e^x-1$
• $\frac{x}{n}\sim \sqrt[n]{x+1}-1$
• $nx\sim (1+x{)}^n-1$
• $1-cosx\sim \frac{x^2}{2}$
• $a^x-1\sim xlna$

(2)

• $x-\sin x\sim \frac{x^3}{6}$
• $\arcsin x-x\sim \frac{x^3}{6}$
• $x-\ln (1+x)\sim \frac{x^2}{2}$
• $\tan x-x\sim \frac{x^3}{3}$
• $x-\arctan x\sim \frac{x^3}{3}$

二、积分中值定理

极值定理

假设m,M是区间[a,b]上的最小最大值，则有
$$m(b-a)\le {\int }_a^{b}f(x)dx\le M(b-a)$$
图文解说：

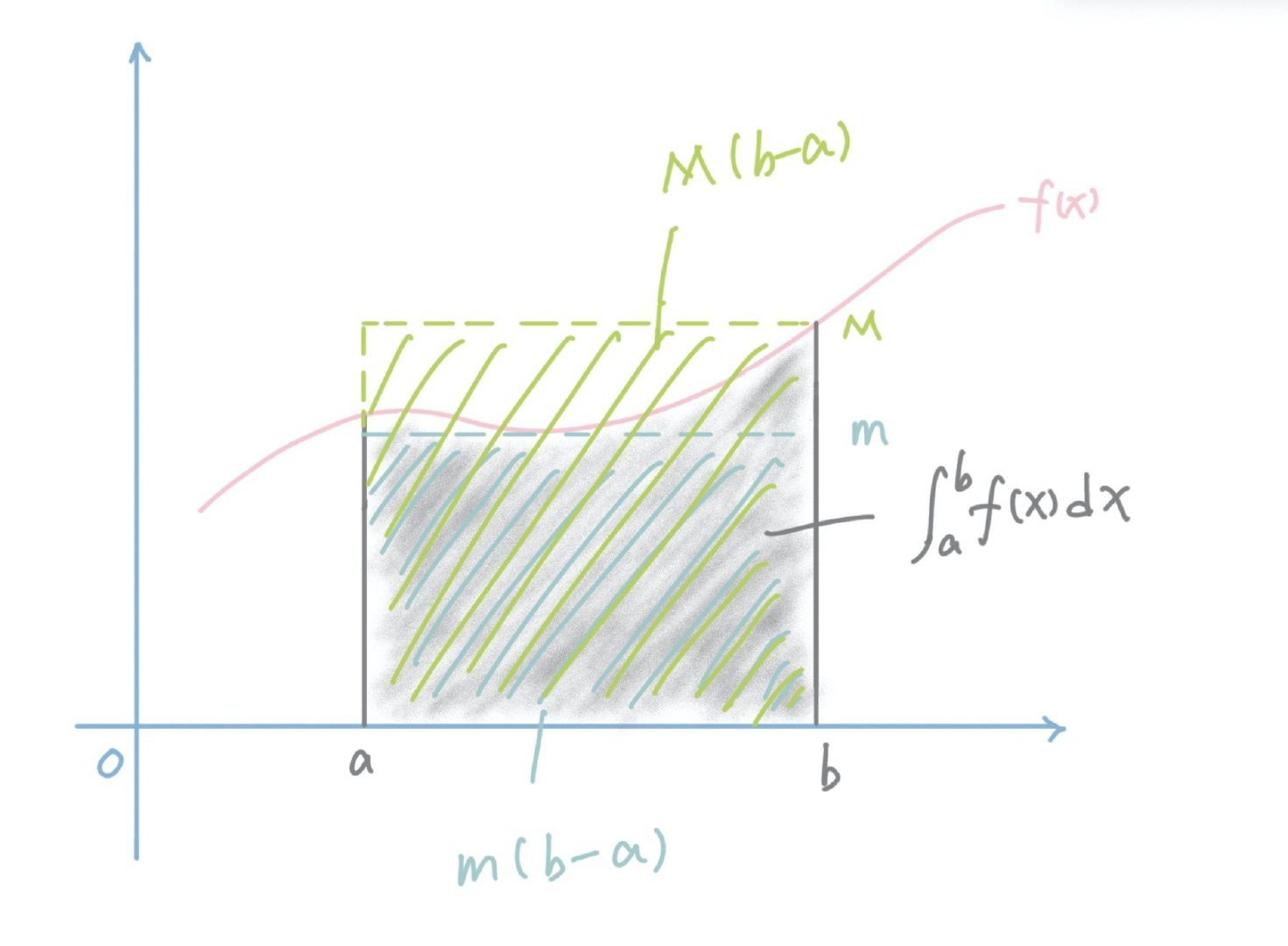
连续函数的介值定理

连续函数的介值定理，它的含义是说对于一个在区间[a, b]上连续的函数，对于任一在其最大值和最小值之间的常数，我们必然可以在区间[a, b]上找到一点，使得该点的函数值等于这个常数。

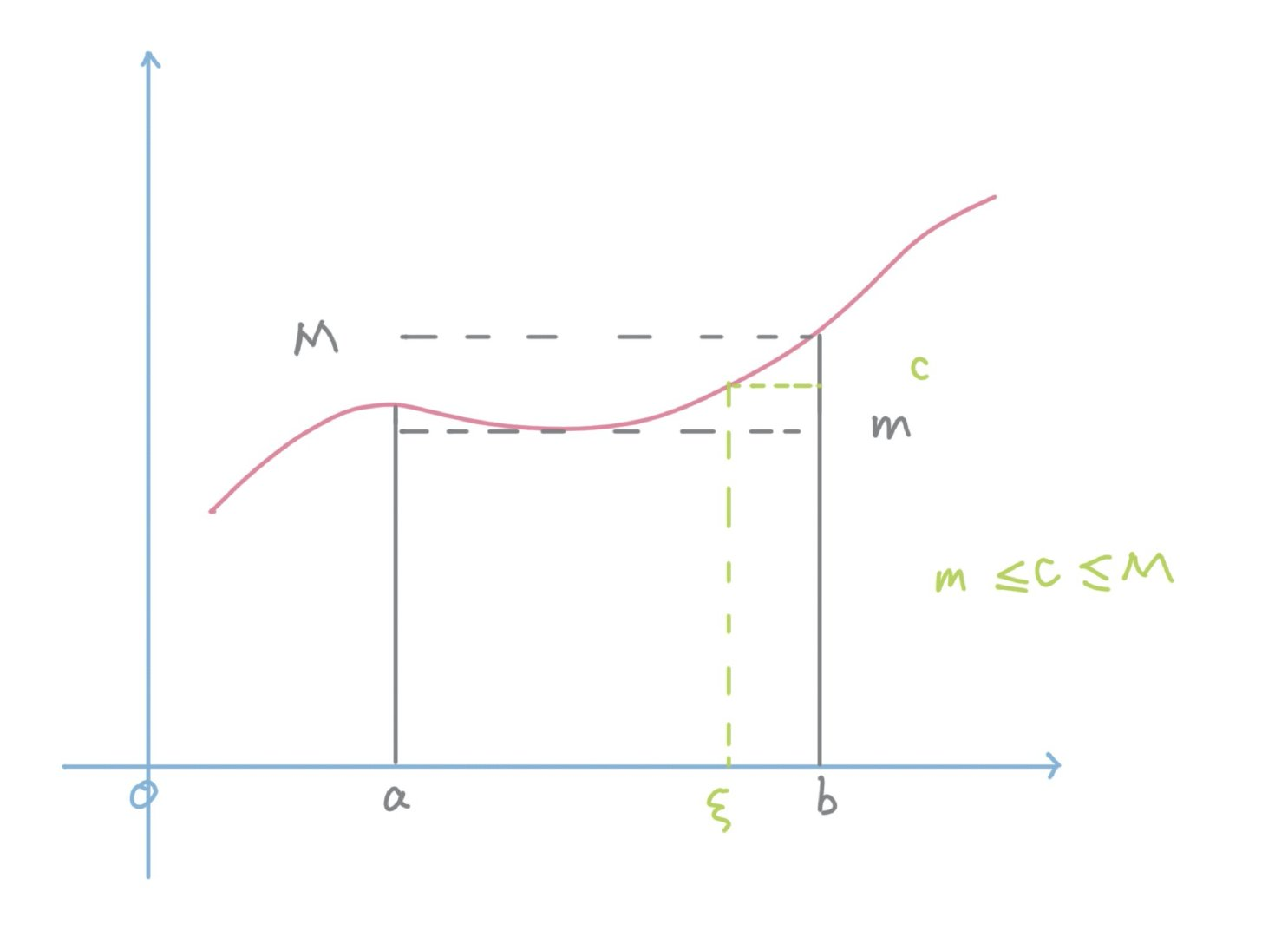
积分中值定理

在极值定理中除以$b-a$ $（b-a\ge 0）$,则有
$$m\le \frac{1}{b-a}{\int }_a^{b}f(x)dx\le M$$,
在$\xi \in [a,b],有$
$$\frac{1}{b-a}{\int }_a^{b}f(x)dx=f(\xi )$$
在乘以$b-a$ $（b-a\ge 0）$,则有
$${\int }_a^{b}f(x)dx=f(\xi )(b-a)$$
图文解说

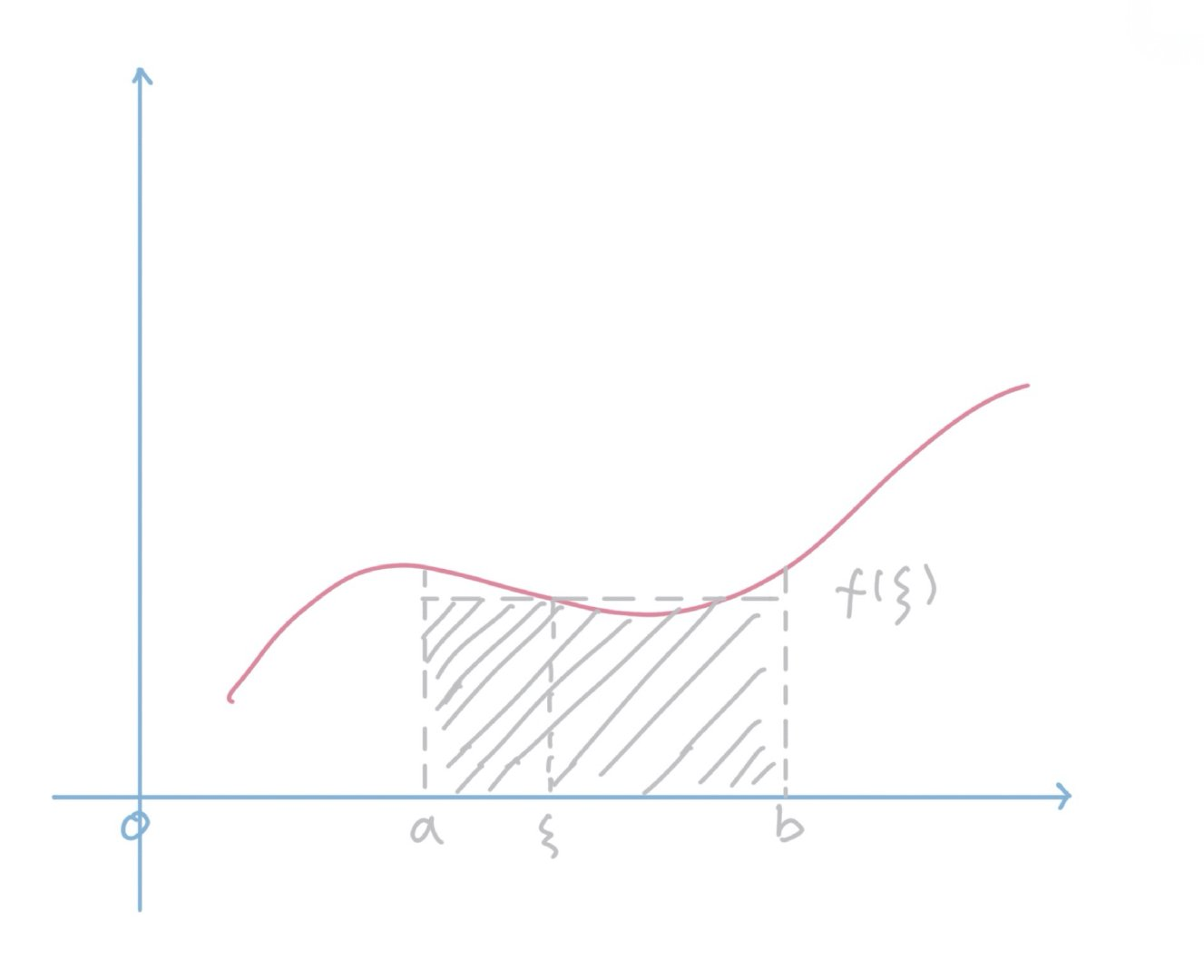
三、连续、可导关系

可导一定连续，连续不一定可导

可导：

• 导数存在
• 左导 = 右导
  $$f_{\Delta x\to 0}^{’}(x)=\frac{f(x)-f(x+\Delta x)}{\Delta x}$$

连续：

• 左极限 = 右极限 = 该点函数值
  $$\underset{\Delta x\to 0}{\lim }f(x+\Delta x)-f(x)=f(x)$$

反例就是$f(x）=|x|$

四、两个重要极限及推导过程

两个重要极限

1. $$\underset{x\to 0}{\lim }\frac{\sin x}{x}=1$$
2. $$\underset{x\to \infty }{\lim }(1+\frac{1}{x}{)}^x=e$$

具体推理过程：两个重要极限

五、常见求导公式

1. $(C{)}^{{}^{\prime }}=0$
2. $(x^a{)}^{{}^{\prime }}=a{x}^{a-1}$
3. $(a^x{)}^{{}^{\prime }}=a^x\ln a$
4. $(e^x{)}^{{}^{\prime }}=e^x$
5. $({\log }_a^x{)}^{{}^{\prime }}=\frac{1}{x\ln a}$
6. $(\ln |x|{)}^{{}^{\prime }}=\frac{1}{x}$
7. $(\sin x{)}^{{}^{\prime }}=\cos x$
8. $(\cos x{)}^{{}^{\prime }}=-\sin x$
9. $(\tan x{)}^{{}^{\prime }}={\sec }^{2}x$
10. $(\cot x{)}^{{}^{\prime }}=-{\csc }^{2}x$
11. $(\sec x{)}^{{}^{\prime }}=\sec x\tan x$
12. $(\csc x{)}^{{}^{\prime }}=\csc x\cot x$
13. $(\arcsin x{)}^{{}^{\prime }}=\frac{1}{\sqrt{1-x^2}}$
14. $(\arccos x{)}^{{}^{\prime }}=-\frac{1}{\sqrt{1-x^2}}$
15. $(\arctan x{)}^{{}^{\prime }}=\frac{1}{1+x^2}$
16. $(arccotx{)}^{{}^{\prime }}=-\frac{1}{1+x^2}$

六、常见奇偶性

奇函数

1. $f(x)=\ln (x+\frac{x}{1+x^2})$

偶函数