目录
1 模型的加载和保存
1.1 保存
- joblib.dump(rf,"test.pkl")
1.2 加载
- estimator=joblib.load("test.pkl")
1.3 代码实现
- fit之后再进行模型的保存
- 加载的模型也有.predict函数也可以进行预测
#正规方程求解方程式预测结果
lr=LinearRegression()
lr.fit(x_train,y_train)
print("这里是回归系数:",lr.coef_)
#保存训练好的模型
joblib.dump(lr,"./tmp/test.pkl")
#预测房价结构或
model=oblib.load("./tmp/test.pkl")
y_predict=std_y.inverse_transform(model.predict(x_test))
print("保存的模型的预测结果:",y_prerdict)2 逻辑回归
2.1 特点
- 线性回归的式子作为输入
- 二分类
- 能获得出概率值
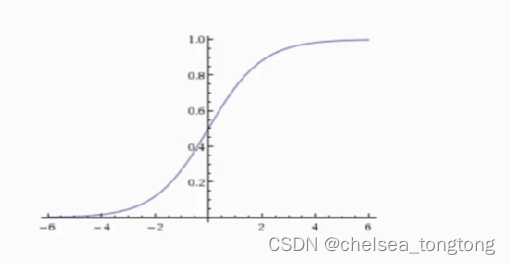
- sigmoid函数输出[0,1]区间的概率值,默认0.5作为阀值(>0.5看成1,<0.5看成0)
2.2 损失函数、优化
2.2.1 损失函数计算

2.2.2对数似然损失计算
真实二分类值:[1,0,0,1]
阈值:0.5
属于1的概率:[0.6,0.1,0.51,0.7]
判断的二分类值:[1,0,1,1]
损失值:1log(0.6)+0log(0.1)+0log(0.51)+1log(0.7)
2.2.3 梯度下降法优化
- 均方误差的损失函数只有一个最小值,而对数似然函数的最小值有多个,所以有局部最小值
- 这是目前解决不了的问题
- 优化的方法是梯度下降法
- 尽量改善的方法:1、多次随机初始化,多次比较最小结果 2、求解过程中,调整学习率
- 尽管没有全局最低点,但是机器学习的效果还是很好的
3 逻辑回归API
sklearn.linear_model.LogisticRegression("penalty"=12,C=1.0)
Logistic:回归分类器
coef_:回归系数
4 逻辑回归预测癌症案例
4.1 数据介绍
数据来源:sIndex of /ml/machine-learning-databases/breast-cancer-wisconsin

数据描述
(1)699条样本,共11列数据,第一列用语检索的id,后9列分别是与肿瘤相关的医学特征,最后一列表示肿瘤类型的数值。
(2)包含16个缺失值,用”?”标出。
4.2 处理数据
- 数据没有列明,所以要把列名加上。
- 列名在breast-cancer-wisdom.names里面找到的,如下
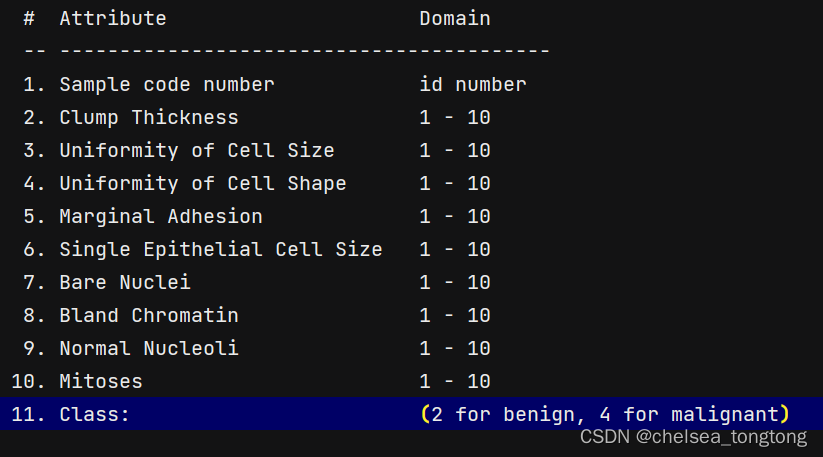
- 增加列名的方法(names=colum_names)

- 目标值不需要标准化处理
- 本来缺失值用?表示,现在用replace函数进行替换,用np.nan替换?
- dropna()用来删除数据中所有的缺失值
#构造列标签名字
column=['Sample code number','Clump Thickness','Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion','Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']
# pd读取数据
data= pd.read_csv("D:\\Download\\breast-cancer-wisconsin.data")
print(data)
#缺失值进行处理
data=data.replace(to_replace="?",value=np.nan)
data= data.dropna()
#进行数据的分割
x_train,x_test,y_train,y_test=train_test_split(data[column[1:10]],data[column[10]],test_size=0.25)
#标准化处理
std=StandardScaler()
x_train=std.fit_transfrom(x_train)
x_test=std.transfrom(x_test)4.3 建立模型
#逻辑回归预测
lg=LogisticRegression(C=1.0)#C=1说明是正则化
lg.fit(x_train,y_train)
print(lg.coef_)4.4 运行结果和准确率及召回率
对于召回率介绍:机器学习笔记--classification_report&精确度/召回率/F1值_阿卡蒂奥的博客-CSDN博客_classification report
- classfication_report()计算召回率
- labels=[2,4]对应着target_names=["良性","恶性"]
y_predict=lg.predict(x_test)
print("模型准确率:",lg.score(x_test,y_test))
print("模型召回率:",classfication_report(y_test,y_predict,labels=[2,4],target_names=["良性","恶性"]))运行结果(准确率):

运行结果(召回率):

准确率不能反映什么,但是看恶性肿瘤的召回率是0.95,说明有5个人被错误得判断成了是恶行肿瘤啦。
5 总结
应用:广告点击率、是否患病、金融诈骗、是否为虚假账号
5.1 优点
适合需要得到一个分类概率的场景,简单,速度快
5.2 缺点
不好处理多分类问题
6 逻辑回归和朴素贝叶斯的区别
| 逻辑回归 | 朴素贝叶斯 | |
| 解决问题 | 二分类 | 多分类 |
| 应用场景 | 二分类需要概率 | 文本分类 |
| 参数 | 正则化力度 | 没有 |
| 相同 | 得出的结果都有概率 | |
| 模型类型 | 判别模型 | 生成模型 |
| 原因 | 没有先验概率 | 有先验概率 |
判别模型:k-近邻、决策树、随机森林、神经网络
生成模型:隐马尔可夫模型
本文含有隐藏内容,请 开通VIP 后查看