目录
原码
1.原码是将数字转换为二进制。
2.原码必须符合八位,如果不满足八位就从右向左补0。(从右往左的最末尾位是符号位根据正负再判断补0或是补1)
3.原码的从右往左的最末尾位是符号位,正数为0,负数为1。
| 数值1 | 数值-1 | 1-1 | |
|---|---|---|---|
| 原码 | 0000 0001 | 1000 0001 | 1000 0010 |
1 - 1 =0000 0001 + 1000 0001 = (1000 0010)2 (二进制,逢二进一)=(-2)10(十进制的-2)
1 - 1 按照常理应该为0,但是此处得出不为0,代表着原码间不可做运算。
反码
1.正数的反码还是原码。
2.负数的反码符号位不变。
2.负数的反码(除符号位)按位取反。
| 数值1 | 数值-1 | 1-1 | |
|---|---|---|---|
| 原码 | 0000 0001 | 1000 0001 | 1000 0010 |
| 反码 | 0000 0001 | 1111 1110 | 1111 1111 |
1 - 1 进行反码运算为1111 1111,对其进行取反(跟取反码操作一致)就可知道其原码是(1000 0000)2 = (-0)10(就为-0)这在一定程度上来说反码间是可以进行运算的,但是0为负来说用反码来进行运算又不太准确。
补码
1.正数的补码还是原码
2.负数的补码= 反码+1
| 数值1 | 数值-1 | 1-1 | |
|---|---|---|---|
| 原码 | 0000 0001 | 1000 0001 | 1000 0010 |
| 反码 | 0000 0001 | 1111 1110 | 1111 1111 |
| 补码 | 0000 0001 | 1111 1111 | 0000 0000 |
这时的1-1便是十进制的 0,代表着补码进行运算是比较准确的。
移码
将符号位转变(正数为1,负数为0)
这是因为在正常逻辑观念里,正数应该比负数大,这样在数轴上面也能更好的表示。也不难发现,这很好的解开了反码间的运算导致0出现负数的情况。
| 数值1 | 数值-1 | 1-1 | |
|---|---|---|---|
| 原码 | 0000 0001 | 1000 0001 | 1000 0010 |
| 反码 | 0000 0001 | 1111 1110 | 1111 1111 |
| 补码 | 0000 0001 | 1111 1111 | 0000 0000 |
| 移码 | 1000 0001 | 0111 1111 | 1000 0000 |
移码间可以进行正常的运算。
表示的范围
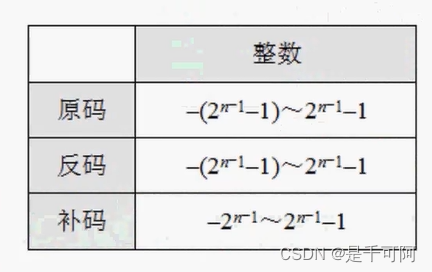
为什么补码会比原码、反码少一位?
| 二进制 | 十进制 | 二进制 | 十进制 | |
|---|---|---|---|---|
| 原码 | 0000 0000 | 0 | 1000 0000 | -0 |
| 反码 | 0000 0000 | 0 | 1111 1111 | -0 |
| 补码 | 0000 0000 | 0 | 0000 0000 | -0 |
原码与反码的0与-0表示不同,而补码的0与-0表示相同,这就是补码比原码、反码少一位的原因。
本文含有隐藏内容,请 开通VIP 后查看