导言: 本文主要使用Pytorch 和 Numpy 实现图的 Adjacency Matrix 与 COO稀疏矩阵(edge_index, 和edge_w)相互转化
1. 图的两种表示方式
1.1 普通邻接矩阵 AdjacencyMatrix
本文所指的图是指Undirected graph G(V, E),并且Adjacency Matrix 如下图F所示。
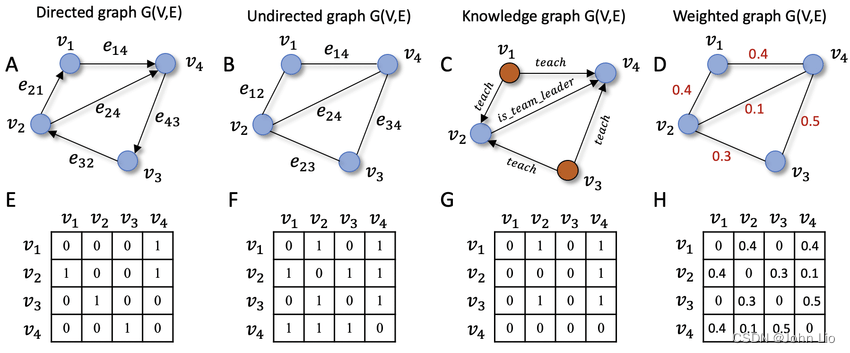
1.2 图的边的连接度和连接权重 edge_index, edge_w,即COO稀疏矩阵
图还可以使用edge_index 和 edge_w 表示,edge_index 为 2*n 的矩阵, edge_w 为 1 * n 的矩阵。
2.实现代码
import torch
import scipy.sparse as sp
import numpy as np
#定义edge_index 和edge_w表示的图
edge_index = torch.tensor([[0, 0, 0, 1, 1, 2, 2, 2, 3, 3],
[1, 2, 3, 0, 2, 0, 1, 3, 0, 2]])
edge_w = torch.rand(10)
#将edge_index 和edge_w扩展成3维的张量,实做中第0维就是表示batch,这里batch_size = 64
big_edge_index = edge_index.unsqueeze(dim = 0)
big_edge_index = big_edge_index.repeat_interleave(64, dim=0)
big_edge_w = torch.rand(64, 10)
n = 64
#将edge_index 和edge_w表示的图 转化成 邻接矩阵表示的图
adj = torch.zeros(64, 4, 4)
for i in range(n):
adj_matrix = sp.coo_matrix(arg1=(big_edge_w[i, :], (big_edge_index[i,0,:], big_edge_index[i,1,:])), shape=(4,4))
adj_matrix = adj_matrix.todense()
adj[i] = torch.from_numpy(adj_matrix)
#邻接矩阵表示的图转化为edge_index 和edge_w表示的图
for j in range(n):
tmp_index = torch.nonzero(adj[j]).T
tmp_data= adj[j][tmp_index[0], tmp_index[1]]
tmp_index = tmp_index.unsqueeze(dim=0)
tmp_data = tmp_data.unsqueeze(dim=0)
if j == 0:
index = tmp_index
data = tmp_data
else:
index = torch.cat([index, tmp_index], dim=0)
data = torch.cat([data, tmp_data], dim=0)
new_edge_index = index
new_edge_w = data
*如有问题和错误请在下方留言。转载请标明出处
参考文章:
本文含有隐藏内容,请 开通VIP 后查看