一、建模
参考资料:https://zhuanlan.zhihu.com/p/137960186
1、三维模型和连杆、关节定义
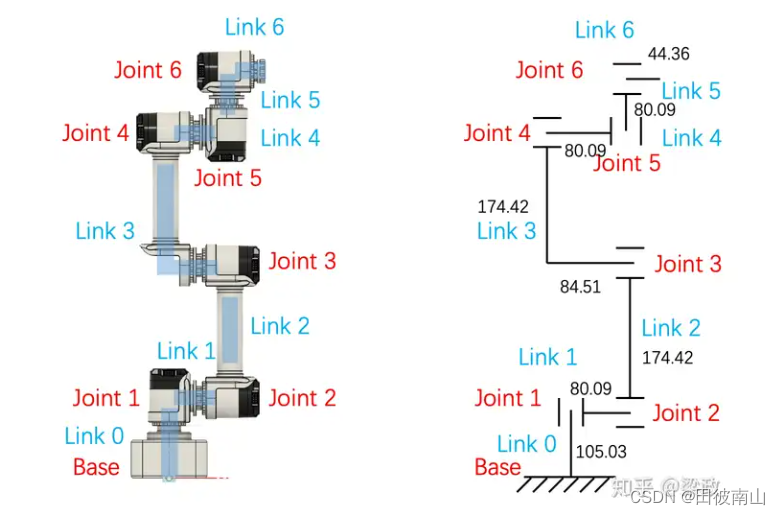
2、设置z轴
- SDH和MDH会不一样,主要的区别在于SDH中坐标系在连杆末端,MDH中坐标系在连杆首端。虽然这里只是给出z轴,但是由于后面原点位置不同,所以二者z轴也不同。

2、设置原点和x轴
| 方法 | SDH | MDH |
|---|---|---|
| 原点 | i和i-1的交线是i原点,如果不想交用公垂线与i交点 | i和i+1的交线是i原点,如果不想交用公垂线与i交点 |
| x轴 | 指向i-1 | 指向i+1原点 |
| 添加 | 0坐标系 | 6坐标系 |
| y轴 | 右手定则 | 右手定则 |
- 关于原点这块我的理解和资料上不同,不知道谁写错了


3、确定dh参数
- SDH和MDH都是由前一坐标系移动到下一坐标系,写i行就是{i-1}到{i}
- 所有角度符合右手螺旋定则的是正方向
- theta是绕z轴转使得x轴重合的角度,d是沿着z轴运动使得x轴重合的距离
(1)SDH
- θ → d → α → a \theta\rightarrow d\rightarrow\alpha\rightarrow a θ→d→α→a

(2)MDH
- α → a → θ → d \alpha\rightarrow a\rightarrow\theta\rightarrow d α→a→θ→d

(3)几何参数

二、正运动学
- 资料:https://blog.csdn.net/subtitle_/article/details/130982929
1、齐次变换矩阵
可以以此计算所有的T,左上的3×3是三个轴,右侧是三维向量是原点坐标
标准DH的齐次变换矩阵

改进dh法的齐次变换矩阵

三、逆运动学
- 资料: https://blog.csdn.net/wh_STUDY/article/details/126862627
- 常用的方法有几何解法、代数解法和数值解法
1、pieper准则
- 如果一个机械臂的结构满足pieper准则,则有封闭解,即可以获得用公式表达的解
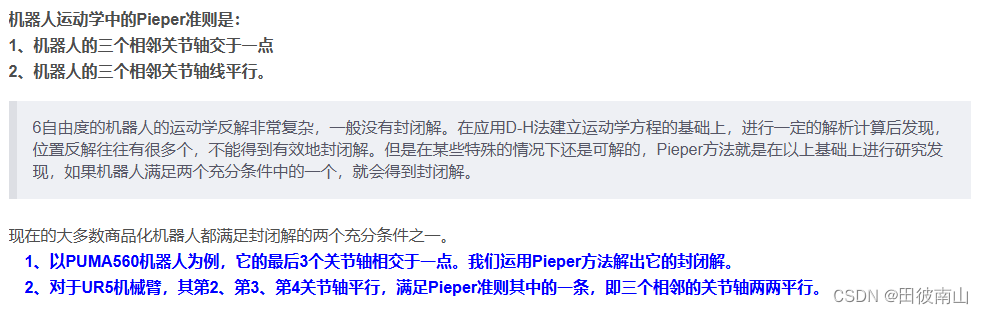
2、几何解
- 几何解直接看参考连接中举得案例,一般很少使用
3、代数解
- 参考资料:工业用六轴机械臂的建模与仿真_卢锐
3.1 改进dh建模


3.2 求代数逆解
- 利用的就是齐次变换矩阵的相乘(一般是在左侧的上下标)
A 6 0 = A 1 0 A 2 1 A 3 2 A 4 3 A 5 4 A 6 5 A^0_6 = A^0_1A^1_2A^2_3A^3_4A^4_5A^5_6 A60=A10A21A32A43A54A65 - 求 θ 1 \theta_1 θ1
A 1 0 − 1 A 6 0 = A 2 1 A 3 2 A 4 3 A 5 4 A 6 5 {A^0_1}^{-1}A^0_6 = A^1_2A^2_3A^3_4A^4_5A^5_6 A10−1A60=A21A32A43A54A65
令两侧的(1,4)和(2,4)分别相等,依次求解其他角度,最终会有8组解