一些sklearn的库的使用:
1. 半监督学习: SelfTrainingClassifier、Label Propagation
2. 特征选择与稀疏学习:
sklearn.feature_selection中 过滤式选择SelectKBest, chi2
包裹式选择SelectFromModel
sklearn.linear_model 中的正则化回归 Lasso, Ridge
3. 聚类:
sklearn.cluster 中的 KMeans 和 DBSCAN
sklearn.mixture 中的 GaussianMixture
4. sklearn.neighbors 中的(KNN) KNeighborsClassifier
5. PCA 以及sparse版本 kernel版本
目录
1.1 SelfTrainingClassifier 自监督训练分类
1. 半监督学习
下例为 先对digits数据中 0~9 每个类别只选 10%的数据保留(模拟少量标记数据情形)
from sklearn.datasets import load_digits
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import numpy as np
# 加载数据
X, y = load_digits(return_X_y=True)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 划分训练集和测试集(保持类别比例)
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42, stratify=y)
# 创建未标注数据(更合理的生成方式)
def create_unlabeled_data(y, unlabeled_ratio=0.9, random_state=42):
#每个类别中的0.9 标记为未标注样本
np.random.seed(random_state)
unlabeled_mask = np.zeros(len(y), dtype=bool)
for class_label in np.unique(y):
class_indices = np.where(y == class_label)[0]
n_unlabeled = int(unlabeled_ratio * len(class_indices))
unlabeled_mask[np.random.choice(class_indices, n_unlabeled, replace=False)] = True
return unlabeled_mask
unlabeled_mask = create_unlabeled_data(y_train, unlabeled_ratio=0.9)
y_train_semi = y_train.copy()
y_train_semi[unlabeled_mask] = -1 # 标记未标注样本
print(f"标注样本数: {sum(y_train_semi != -1)}")
print(f"未标注样本数: {sum(y_train_semi == -1)}")1.1 SelfTrainingClassifier 自监督训练分类
在基础模型的基础上 加上SelfTrainingClassifier 进行数据标注 重新训练模型

SVC(支持向量分类)外套着SelfTrainingClassifier; 不断增添伪标记
from sklearn.semi_supervised import SelfTrainingClassifier
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, classification_report
# 创建并训练自训练分类器
base_svm = SVC(
kernel='rbf',
probability=True, # 必须支持概率预测
class_weight='balanced', # 处理可能的类别不平衡
random_state=42
)
self_training = SelfTrainingClassifier(
base_svm,
threshold=0.75, # 高置信度阈值,减少错误传播
criterion='threshold',
max_iter=50,
verbose=True # 显示训练过程
)
self_training.fit(X_train, y_train_semi)
# 评估模型
y_pred = self_training.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("\n测试集准确率: {:.4f}".format(accuracy))
print(classification_report(y_test, y_pred))
# 查看自训练过程信息
print("\n自训练过程统计:")
print(f"最终迭代次数: {self_training.n_iter_}")
print(f"终止条件: {self_training.termination_condition_}")
print(f"新增伪标签样本数: {sum(self_training.labeled_iter_ > 0)}")1.2 Label Propagation 标签传播
(1)构建数据样本之间的相似图
RBF核:生成全连接图(密集矩阵) KNN核:生成稀疏图(仅保留k个最近邻连接)
(2)标签传播过程
LabelPropagation:完全信任初始标签(alpha=1)
LabelSpreading:多一个参数 通过alpha控制标签可信度(默认0.8表示保留80%初始标签权重)
from sklearn.semi_supervised import LabelSpreading
from sklearn.metrics import accuracy_score, classification_report
label_spread = LabelSpreading(
kernel='knn', # 使用K近邻构建相似图(比RBF更适合数字数据)
n_neighbors=7, # 增加近邻数提高稳定性
alpha=0.8, # 标签保留强度(0.8=80%信任原始标签)
max_iter=30, # 增加迭代次数确保收敛
tol=1e-3, # 早停容忍度
)
label_spread.fit(X_train, y_train_semi)
# 评估模型
y_pred = label_spread.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("\n测试集准确率: {:.4f}".format(accuracy))
print("分类报告:\n", classification_report(y_test, y_pred))
# 查看标签传播效果
print("\n标签传播统计:")
print(f"实际使用的标注样本数: {sum(label_spread.label_distributions_[:, -1] == 0)}")
print(f"模型迭代次数: {label_spread.n_iter_}")2. 特征选择与稀疏学习
周志华《机器学习导论》第11章 特征选择与稀疏学习-CSDN博客
2.1 过滤式选择特征 挑k个特征
SelectKBest — scikit-learn 1.7.1 documentation
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest, chi2
# 加载数据集
X, y = load_iris(return_X_y=True)
# 创建SelectKBest实例
selector = SelectKBest(chi2, k=2)
# 进⾏过滤式特征选择
X_new = selector.fit_transform(X, y)
# 获取所选特征的索引
selected_features = selector.get_support(indices=True)
print("Selected features:", selected_features)2.2 包裹式选择 确定模型后选择
SelectFromModel — scikit-learn 1.7.1 documentation
下例为 先确定一个L1逻辑回归 再对clf包裹式选择特征
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
# 加载数据集
X, y = load_iris(return_X_y=True)
# 创建Logistic回归模型实例
clf = LogisticRegression(solver='liblinear', penalty='l1', C=0.5)
# 创建SelectFromModel实例
selector = SelectFromModel(clf, threshold='mean')
# 进⾏包裹式特征选择
X_new = selector.fit_transform(X, y)
# 获取所选特征的索引
selected_features = selector.get_support(indices=True)
print("Selected features:", selected_features)2.3 嵌入式选择与L1正则化
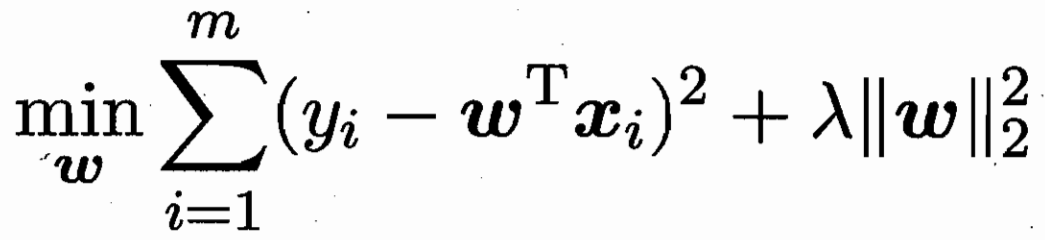
Lasso L1 稀疏解 Ridge L2 模型中(alpha)为正则化前的系数
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso, Ridge
# 加载数据集
X, y = load_iris(return_X_y=True)
X_train, test_x, y_train, test_lab = train_test_split(X,y,test_size = 0.4,random_state = 42)
# 创建Lasso和ridge回归模型
lasso = Lasso(alpha=0.1)
ridge = Ridge(alpha=1.0)
# 进⾏嵌⼊式特征选择
lasso.fit(X_train, y_train)
ridge.fit(X_train, y_train)
# 输出所选特征的系数
coef = lasso.coef_
print("Feature coefficients:", coef)
coef1 = ridge.coef_
print("Feature coefficients:", coef1)
#预测
lasso_pred = lasso.predict(test_x)
ridge_pred = ridge.predict(test_x)
# 计算并打印评分(R²分数)
print("\nModel Performance:")
print(f"Lasso R² score: {lasso.score(test_x, test_lab):.4f}")
print(f"Ridge R² score: {ridge.score(test_x, test_lab):.4f}")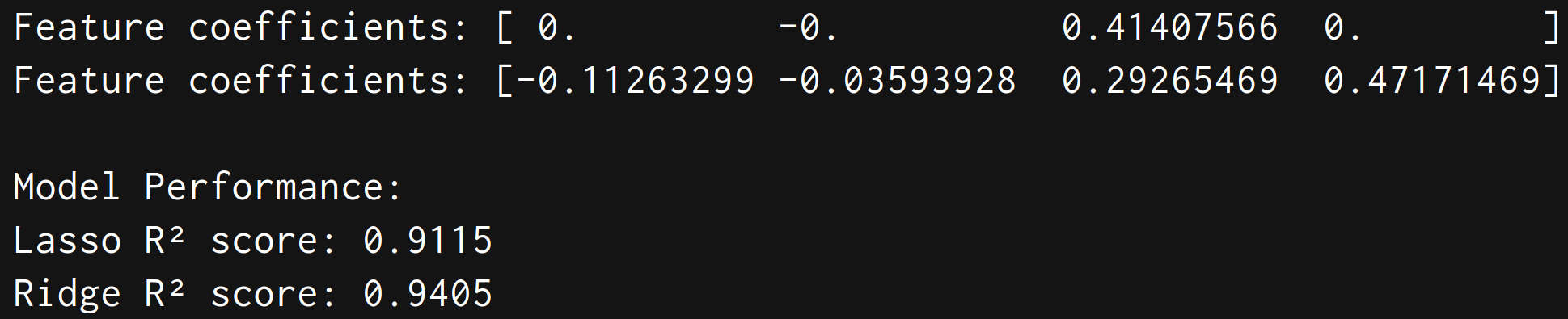
3. 聚类
3.1 K-means
k_means — scikit-learn 1.7.1 documentation

输入参数:
n_clusters: 要形成的簇数量,也是要生成的中心点数量
init: 初始化方法
'k-means++' (默认): 智能初始化,加速收敛
'random': 随机选择初始中心点
也可以直接传入初始中心点坐标
n_init: 运行算法的次数(使用不同初始种子),最终选择最佳结果
'auto': 根据init自动选择(随机初始化运行10次,k-means++运行1次)
max_iter: 单次运行的最大迭代次数(默认300)
tol: 收敛阈值(连续两次迭代中心点变化的Frobenius范数)
输出:
cluster_centers_: 簇中心坐标
labels_: 每个样本的簇标签
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
# 加载数据集
X = load_iris().data
# 数据预处理
X_scaled = StandardScaler().fit_transform(X)
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X_scaled)
# 获取聚类结果
print("Cluster labels:", kmeans.labels_)3.2 DBSCAN
DBSCAN — scikit-learn 1.7.1 documentation
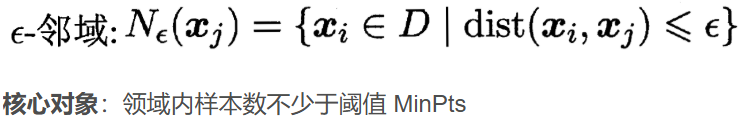
输入参数:
eps邻域半径阈值,决定样本邻域范围min_samples核心点所需邻域内最少样本数metric距离度量方式,可选:- 'euclidean'(欧氏距离)- 'precomputed'(预计算距离矩阵)
输出:
- core_sample_indices_ 核心样本的索引 [n_core_samples]
- components_ 核心样本的特征值 [n_core_samples, n_features]
- labels_ 样本的簇标签(噪声点标记为-1) [n_samples]
from sklearn.cluster import DBSCAN
import numpy as np
X = np.array([[1, 2], [2, 2], [2, 3],
[8, 7], [8, 8], [25, 80]])
clustering = DBSCAN(eps=3, min_samples=2).fit(X)
print(clustering.labels_) # 输出: [ 0 0 0 1 1 -1]3.3 GMM 高斯混合聚类
GaussianMixture — scikit-learn 1.7.1 documentation
输入参数:
- n_components 高斯混合成分数量
- covariance_type 协方差矩阵类型: - 'full': 每个成分有自己的完全协方差矩阵 - 'tied': 所有成分共享相同协方差矩阵 - 'diag': 每个成分有对角协方差矩阵 - 'spherical': 每个成分有单一方差
- tol EM算法的收敛阈值
- reg_covar 协方差对角线的正则化项
- max_iter 最大迭代次数
- n_init 初始化次数
输出:
- weights_ 每个混合成分的权重 [n_components]
- means_ 每个成分的均值 [n_components, n_features]
- covariances_ 协方差矩阵(形状取决于covariance_type)
- predict(X) 预测样本所属成分
- predict_proba(X) 预测样本属于各成分的概率
import numpy as np
from sklearn.mixture import GaussianMixture
X = np.array([[1, 2], [1, 4], [1, 0], [10, 2], [10, 4], [10, 0]])
gm = GaussianMixture(n_components=2, random_state=0).fit(X)
print(gm.means_)
print(gm.predict([[0, 0], [12, 3]]))
print(gm.predict_proba([[0, 0], [12, 3]]))4. sklearn.neighbors 邻居算法
sklearn.neighbors — scikit-learn 1.7.1 documentation
4.1 找最近的邻居
KDTree 递归地将 k维空间 沿数据方差最大的维度(坐标轴)进行二分,形成超矩形区域
BallTree 递归地将空间划分为 超球体(Hypersphere),每个节点代表一个球体区域。
4.2 KNN 最近k个邻居投票
KNeighborsClassifier — scikit-learn 1.7.1 documentation
- n_neighbors 参与投票的最近邻居数量(K值)。
- weights 权重设定 -'uniform':所有邻居权重相等。 - 'distance':权重为距离的倒数(越近影响越大)。- 自定义函数:输入距离数组,返回权重数组。
- algorithm 邻居搜索算法: - 'ball_tree'/'kd_tree':基于树结构,适合高维数据。 - 'brute':暴力搜索,适合小数据集。 - 'auto':自动选择最优算法。
- metric 距离度量标准。常见选项: - 'euclidean'(L2)、'manhattan'(L1)。
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
#加载数据集
data, target = load_digits(return_data_target=True)
#将数据集拆分为训练集(75%)和测试集(25%):
train_x, test_x, train_y, test_y = train_test_split(data, target, test_size=0.25, random_state=33)
knn = KNeighborsClassifier()
knn.fit(train_x, train_y)
predict_y = knn.predict(test_x)
#计算模型准确度
score = accuracy_score(test_y, predict_y)
print(score)5. PCA 主成分分析
先用make_blobs 生成几个簇集合
pca = PCA(n_components=k) 可以指定维度k (≥1的话)
pca = PCA(n_components=0.95) 也可以指定解释的 方差比例之和至少解释多少 (<1的话)
pca = PCA(n_components=‘mle’) 基于最大似然估计自动选择维度
n_components_ 降维后的维度
explained_variance_ 降维后每个维度解释的方差
explained_variance_ratio_ 降维后每个维度解释的比例
from sklearn.datasets import make_blobs
# X为样本特征,Y为样本簇类别, 共10000个样本,每个样本3个特征,共4个簇
X, y = make_blobs(n_samples=10000, n_features=3, centers=
[[3,3, 3], [0,0,0], [1,1,1], [2,2,2]], cluster_std=[0.2, 0.1, 0.2, 0.2], random_state =9)
#我们先不降维,只对数据进行投影,看看投影后的三个维度的方差分布,代码如下:
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
#现在我们来进行降维,从三维降到2维,代码如下:
pca = PCA(n_components=2)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
#现在我们看看不直接指定降维的维度,而指定降维后的主成分方差和比例。
print('n_components=0.95')
pca = PCA(n_components=0.95)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
print(pca.n_components_)
print('n_components=0.99')
pca = PCA(n_components=0.99)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
print(pca.n_components_)
print('n_components=mle')
pca = PCA(n_components='mle')
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
print(pca.n_components_)核化PCA降维 KernelPCA fit_transform(X)
稀疏 SparsePCA 选每个成分的时候 只有部分特征有贡献
from sklearn.decomposition import KernelPCA
from sklearn.datasets import load_iris
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 创建KernelPCA实例
kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
# 进⾏核化线性降维
X_kpca = kpca.fit_transform(X)
from sklearn.decomposition import SparsePCA
spca = SparsePCA(n_components=2, alpha=1, random_state=42)
spca.fit(X)
print("稀疏主成分:\n", spca.components_)
X_spca = spca.transform(X) 