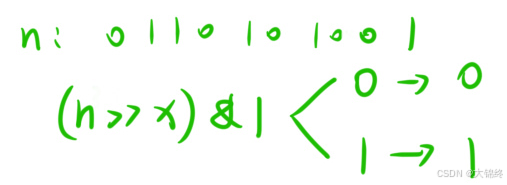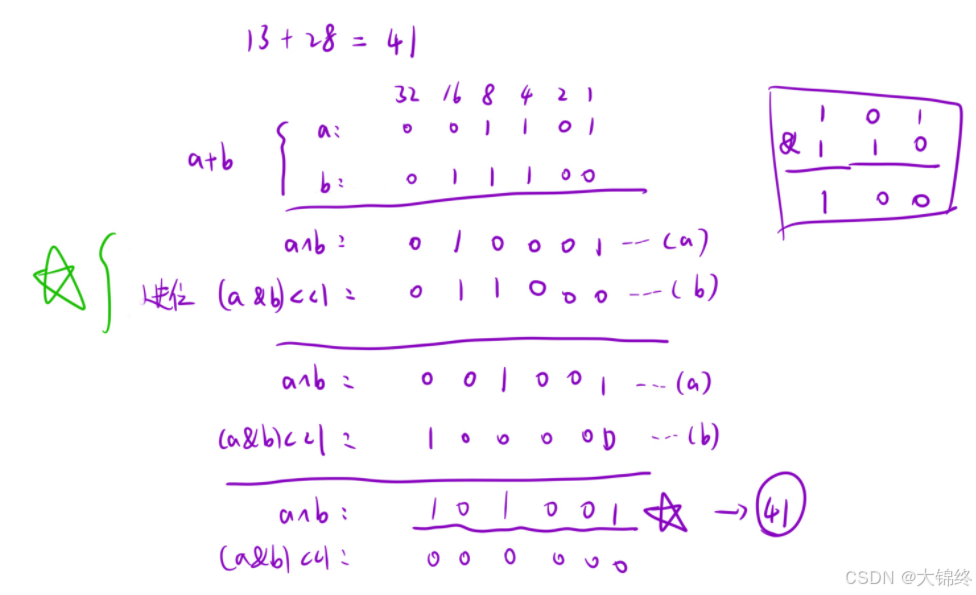1.常见位运算总结
1.1基础位运算
左移(<<)
规则:
将二进制位整体向左移动 n 位,高位溢出丢弃,低位补 0。
公式:a << n 等价于 a * 2^n(无溢出时)。
示例:
5 << 2(二进制:101 << 2 = 10100),结果为 20(5 × 2² = 20)。
用途:
快速乘法(乘以 2 的幂);
构建位掩码(如 1 << 3 生成 0b1000)
右移(>>)
规则:
逻辑右移:无符号数,向右移动 n 位,高位补 0,低位丢弃。
算术右移:有符号数,向右移动 n 位,高位补符号位(保持正负不变),低位丢弃。
公式:a >> n 等价于 a / 2^n(向下取整,无溢出时)。
示例:
无符号数 8 >> 2(1000 >> 2 = 0010),结果为 2;
有符号数 -8 >> 2(假设 8 位补码 11111000 >> 2 = 11111110),结果为 -2。
有符号数以补码形式存储,8 位有符号数的范围是 -128 ~ 127。
正数的补码 = 原码(二进制本身);
负数的补码 = 原码(符号位不变)取反 + 1(末位加 1)。
用途:
快速除法(除以 2 的幂);
提取高位数据(如 (num >> 4) & 0x0F 提取高 4 位)。
按位与(&)运算
规则:两个对应位都为 1 时,结果位为 1;否则为 0。
示例:5 & 3 的计算(二进制:101 & 011 = 001),结果为 1。
记忆口诀:有0就是0
按位或(|)运算
规则:两个对应位中至少有一个为 1 时,结果位为 1;否则为 0。
示例:5 | 3 的计算(二进制:101 | 011 = 111),结果为 7。
记忆口诀:有1就是1
按位异或(^)
规则:两个对应位不同时,结果位为 1;相同则为 0。
示例:5 ^ 3 的计算(二进制:101 ^ 011 = 110),结果为 6。
记忆口诀:
1.相同为0,相异为1
2.无进位相加:
将二进制数对应位按加法规则相加,结果超出1 产生进位就不进位并且将当前位置0,简单说就是出现两次的数相消为0,决定了异或运算具有交换律(本质是出现偶数次的数相消,奇数次保留)
按位取反(~)
规则:将二进制位 0 变为 1,1 变为 0(单目运算)。
示例:~5 的计算(假设为 8 位:~00000101 = 11111010),结果为 -6(补码表示)。
1.2确定数n二进制表示中的第x位是0还是1
既可以将原数右移,也可以将计算数左移再进行位运算
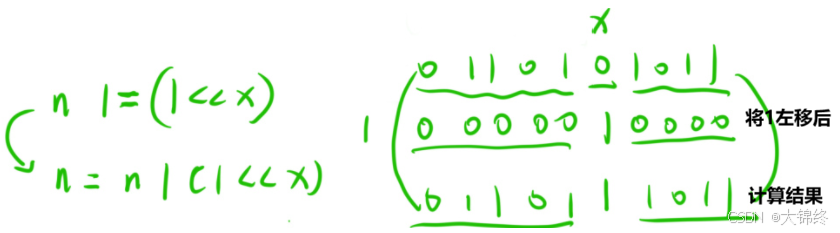
1.3将数n的二进制表示的第x位修改成1
1.因为只能将第x位修改其他位置保持不变,所以移动操作数来计算,原数不动
2.或运算规则有1则为1,操作数不会影响原数,计算结果由原数决定
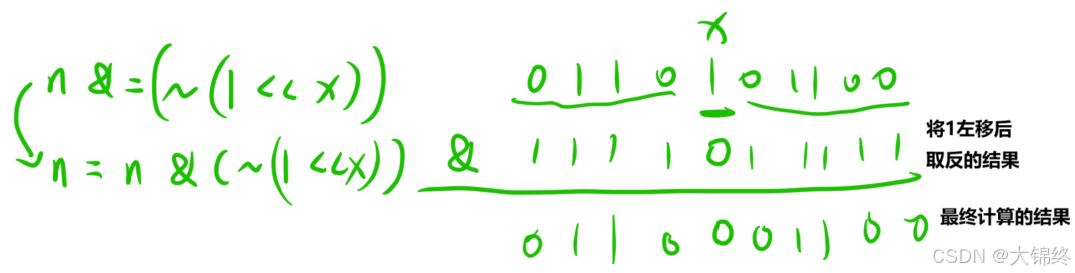
1.4将数n的二进制表示的第x位修改成0
分析过程与上题一模一样
1.5位图的思想
位图(BitMap)思想是一种利用二进制位(bit)的 0/1 状态来标记数据存在性、属性或状态的高效数据结构。它的核心是用 1 个 bit 位表示 1 个数据的状态(如 “存在” 或 “不存在”),结合位运算(与、或、异或、移位等)实现高效的查询、插入、删除等操作。
空间映射:
将一个整数 x 映射到位图中的某个 bit 位。例如,用第 x 位的 1 表示 x 存在,0 表示 x 不存在。
空间效率:
1 个字节(8bit)可表示 8 个整数的状态,相比用数组存储整数,空间效率提升约 32 倍(32 位整数)或 64 倍(64 位整数)
假设需要处理范围为 0~N-1 的整数,位图可通过一个整数数组实现(数组元素为 unsigned int,每个元素占 32bit):
- 核心映射关系
对于整数 x,它在数组中的索引为:index = x / 32(每个 unsigned int 管理 32 个 bit)。
它在该索引元素中的位位置为:bit_pos = x % 32(0~31)
解决位运算问题
类型 1:数组去重(保留唯一元素)
场景:给定一个整数数组(元素范围 0~1000),去除重复元素,保留所有出现过的数。
位图解法:用位图标记元素是否出现过,出现过的元素只保留一次
类型 2:查找数组中只出现一次的元素
场景:数组中除一个元素只出现一次外,其余元素均出现两次,找出该元素。
位图解法:利用异或的性质(xx=0,x0=x),结合位图记录状态。
类型 3:统计范围内的整数个数
场景:统计 [a, b] 区间内出现过的整数个数(已知所有整数范围 0~N)。
位图解法:遍历位图中 a~b 对应的 bit 位,统计为 1 的个数。
类型 4:快速判断两个集合的交集
场景:判断两个整数集合 A 和 B 是否有交集(元素范围 0~1000)。
位图解法:用两个位图分别标记 A 和 B 的元素,通过位与(&) 操作判断是否有同时为 1 的位(即交集)。
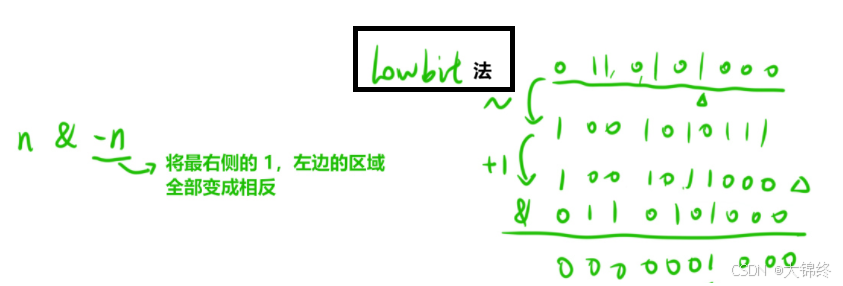
1.6提取数n二进制表示中的最右侧的1
1.7干掉数n二进制表示中的最右侧的1
1.8位运算的优先级
位运算的优先级较低,低于算术运算(如 +、*)和关系运算(如 <、==)
能加括号就加括号,方便省事不用记忆绝不出错
2. (191.)位1的个数
法1:循环检查二进制位
直接循环检查给定整数 n 的二进制位的每一位是否为 1。具体代码中,当检查第 i 位时,我们可以让 n 与 2^i进行与运算,当且仅当 n 的第 i 位为 1 时,运算结果不为 0。
class Solution {
public:
int hammingWeight(uint32_t n) {
int ret = 0;
for (int i = 0; i < 32; i++) {
if (n & (1 << i)) {
ret++;
}
}
return ret;
}
};
法2:位运算优化
运用1.7中总结的公式,将数n最低位的1依次变为0,位1的个数可等价转为执行该公式多少次
class Solution {
public:
int hammingWeight(int n) {
int ret=0;
while(n)
{
n&=n-1;
ret++;
}
return ret;
}
};
3. (338.)比特位计数

同样采取1.7中不断去除最低位1,通过计算次数来确定一个数的二进制位有多少个1,该题给定一个连续数的范围,在计算的外围还要套一层循环来表示数的范围来一次进行计算
class Solution {
public:
vector<int> countBits(int n) {
vector<int> ret(n+1);
for(int i=0;i<=n;i++)
{
int num=0;
//用临时变量来替代i计算,避免i被修改
int x=i;
while(x)
{
x&=x-1;
num++;
}
ret[i]=num;
}
return ret;
}
};
4. (461.汉明距离)
目标是求两数的二进制位有多少位是不同的,可以先用异或运算进行转化,相同为0相异为1,最终再运用1.7中公式计算这个数中有多少位是1就代表原两数中有多少位不同
class Solution {
public:
int hammingDistance(int x, int y) {
x^=y;
int ret=0;
while(x) x&=x-1,ret++;
return ret;
}
};
5. (260.)只出现一次的数字III

1.因为数组其他元素均出现两次,异或后会相互抵消,剩下结果就是两个目标元素的异或结果
2.int x=(sum==INT_MIN?INT_MIN:sum&(-sum));
该运算能保留最低位的1,其余位变为0,因为a、b异或结果不为0在这一位上必然一个为0一个为1,所以可以用这一位作为分组依据;该表达式还有防溢出的作用,对 INT_MIN 取负数 的操作上就是补码取反再加1,INT_MIN 是 int 能表示的最小负数:-2147483648(二进制补码为 10000000 00000000 00000000 00000000),在 C++ 中,对 INT_MIN 取负会导致 有符号整数溢出,这属于 “未定义行为”,因为整数取值范围为左闭右开,所以等于 INT_MIN 取负结果就溢出,所以当 sum 是 INT_MIN 时,直接将 x 赋值为 INT_MIN(无需计算 -sum,避免溢出)
3.用x(最低位的 1)对所有元素分组,最终结果会被分到不同组
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
int sum=0;
for(auto e:nums) sum^=e;
//位的分组表示+防止溢出
int x=(sum==INT_MIN?INT_MIN:sum&(-sum));
//分组遍历找到不同的两个数
int num1=0,num2=0;
for(auto e:nums)
{
if(e&x) num1^=e;
else num2^=e;
}
return {num1,num2};
}
};
5. (260.)只出现一次的数字II

class Solution {
public:
int singleNumber(vector<int>& nums) {
int ret=0;
for(int i=0;i<=31;i++)//处理32位整数的每一位
{
int total=0;//统计第i位的总大小
for(auto num:nums)
{
total+=((num>>i)&1);
}
if(total%3==1)
{
ret|=(1<<i);
}
}
return ret;
}
};
思路:
对于数组中出现三次的元素,它们的每个二进制位(0 或 1)也会出现三次;而唯一出现一次的元素,其二进制位会让对应位置的总计数 “无法被 3 整除”。通过统计每个二进制位(0~31 位,对应 32 位整数)的出现次数,若某一位的总次数模 3 余 1,则说明该位是目标元素的二进制中为 1 的位。
也可以用哈希表但空间复杂度为O(N)
6. ⾯试题 01.01. 判定字符是否唯⼀

算法思路:
利⽤位图的思想,每⼀个⽐特位代表⼀个字符,⼀个 int 类型的变量的 32 位⾜够表⽰所有的⼩写字⺟。⽐特位⾥⾯如果是 0 ,表⽰这个字符没有出现过。⽐特位⾥⾯的值是 1 ,表⽰该字符出现过。那么我们就可以⽤⼀个整数来充当哈希表。
class Solution
{
public:
bool isUnique(string astr)
{
// 利⽤鸽巢原理来做的优化
if(astr.size() > 26) return false;
int bitMap = 0;
for(auto ch : astr)
{
int i = ch - 'a';
// 先判断字符是否已经出现过
if(((bitMap >> i) & 1) == 1) return false;
// 把当前字符加⼊到位图中
bitMap |= 1 << i;
}
return true;
}
};
7. (268.) 丢失的数字

如果我们把数组中的所有数,以及 [0, n] 中的所有数全部异或在⼀起,那么根据异或运算的「消消乐」规律,最终的异或结果应该就是缺失的数
class Solution {
public:
int missingNumber(vector<int>& nums) {
int ret=0;
for(auto num:nums) ret^=num;
for(int i=0;i<=nums.size();i++) ret^=i;
return ret;
}
};
也可以用高斯公式公式计算((nums.size())*(nums.size()+1))/2-sum;
8. (371.)两整数之和

异或 ^ 运算本质是⽆进位加法;按位与 & 操作能够得到进位;然后⼀直循环进⾏,直到进位变成 0 为⽌。
由于计算的是进位,所以结果要左移一位,同时要将类型强转为无符号整型,因为如果操作数是负数(即符号位为 1),其行为是未定义的
class Solution {
public:
int getSum(int a, int b) {
while(b)
{
int sum=a^b;//算出无进位相加的结果
b=(unsigned int)((a&b)<<1);//算出进位的结果
a=sum;
}
return a;
}
};
9. ⾯试题 17.19. 消失的两个数字

本题就是 268. 丢失的数字 + 260. 只出现⼀次的数字 III 组合起来的题。
先将数组中的数和 [1, n + 2] 区间内的所有数异或在⼀起,问题就变成了:有两个数出现了⼀次,其余所有的数出现了两次。进⽽变成了该题
class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
//异或所有元素,找出消失的两个数字的异或结果
int sum=0;
for(auto num:nums) sum^=num;
for(int i=1;i<=nums.size()+2;i++) sum^=i;
//设定比特位标志来分组
int x=(sum==INT_MIN?INT_MIN:sum&(-sum));
int num1=0,num2=0;
//分组计算异或结果
for(auto num:nums)
{
if(x&num) num1^=num;
else num2^=num;
}
for(int i=1;i<=nums.size()+2;i++)
{
if(x&i) num1^=i;
else num2^=i;
}
return {num1,num2};
}
};