关于多脉冲(相干&非相干)积累问题探讨--仿真和实测数据实践-易微帮

说明

积累这两个字往宽泛了说，它在信号处理中有诸多相关的应用：比如在采样的过程中，采样率不变的前提下增加采样点数(采样时间)是一种积累，由此我们可以获得更高的频率分辨率；在DOA估计中，多帧的采集是一种积累，由此我们可以估计得到更准确的协方差矩阵以更好地使用各类多快拍超分辨率测角算法；本文试图讨论的多脉冲积累则是信号处理中讨论更广泛的概念。

我很早前在博文[1]: 毫米波雷达信号处理中的通道间相干与非相干积累问题-CSDN博客中对该话题有过一些探讨，那篇博文讨论的是雷达通道之间的积累，通道间的积累问题算是多脉冲积累的一个延伸，两者之间无本质差别。现在回过头去看那篇博文是存在一些问题的，最近的工作刚好涉及到脉冲积累，我们采集了一些数据做验证，于是借此机会对脉冲积累问题做一些梳理(从仿真和实测数据两个角度)，同时对博文[1]存在的一些问题做一些解释。

Blog

2024.4.19 博文第一次撰写

一、多脉冲积累综述&问题明确

绝大多数情况下，我们是无法从雷达单脉冲下的目标回波数据中检测到目标的，所以我们需要收发多个脉冲进行积累以提高SNR，才能让我们能够检测到目标。SNR的抬升是多脉冲积累的核心目标，也是后文的仿真和实测数据想要验证和量化的东西。

在进入后续的讨论之前，首先明确一下SNR的定义：我在博文[1]中很粗心地把SNR理解成目标幅值和噪声幅值的比，但SNR的定义实际为目标功率和信号功率的比值！我们一般取10倍的lg:

(1-1)

当然，功率为幅值的平方，所以上式也可以写成幅值A的表达式：

(1-2)

收发多脉冲只是我们获取多脉冲数据的手段，我们如何进行积累(如何利用这些多脉冲下的数据)？基于我们是否利用多脉冲之间的相位信息可以将脉冲积累分相干(参)积累和非相干积累。其实对于单脉冲信号做距离压缩也是一种相干积累[3](比如在车载毫米波雷达中我们对去斜解调后的chirp回波做FFT可以使得目标对应距离的频点出现波峰)。

具体地[2]，相干(参)积累是指：将同一距离门上的回波脉冲序列的幅值和相位进行叠加，这种方法称为相参积累。进行相参积累时必须要保证回波脉冲之间的高频相位具有相互确定的关系，即回波脉冲信号是相参的，在这种情况下，接收信号在发射信号解调后，经过一定处理就可以得到准确的多普勒频移。因为零中频信号保留了信号的相位和幅度信息，所以相参积累一般是在零中频对信号复包络进行的。非相干积累是指：在非相参积累中，每个采样的时间和幅度不一定相同，因此不需要考虑采样点之间的相位关系。也叫“检波后累积”，或者“视频累积”（Video Integration），比检波前累积更容易完成，因为不需要保存回波的相位，只需要将脉冲的包络对准就可以相加。在操作上，可以直接对信号取幅值后累加，或者像[1]中那样，取平方后累加。

理论上，N个脉冲下相干(参)积累下的SNR可以提升N倍，而非相干积累对SNR没有提高！(不过当SNR大于0dB时，可以拉开信号与噪声之间的幅值差)。参考资料[2]中有一些证明，我截取了部分放在这里：

对于相干积累，我们假设有N个脉冲信号，每个信号内含目标回波、噪声等信号，噪声信号的相位分布是随机的，且各脉冲信号之间的噪声也满足统计独立的条件，因此，噪声积累的效果是平均功率之和，也即N个脉冲积累后噪声功率是单个脉冲噪声功率的N倍。而对于信号而言，各脉冲信号是严格按照相位关系进行同相相加的，因此积累的结果是信号电压提升了N倍，功率则提升N^2，于是由SNR的定义可知，积累后的SNR提升了N倍：

(1-3)

(1-4)

后文将从仿真和实测数据两个方面对相干和非相干积累对SNR提高的效果进行量化。

二、仿真方案以及仿真结果

2.1 相干&非相干积累下噪声幅值和功率的变化

本节仿真单独验证噪声幅值和平均功率随积累的变化：我们随机生成10000个长度为256的高斯白噪声复数信号脉冲(均值为0，方差为1)，然后分别通过：直接相加、取模后相加、取平方后相加的方式，分别累加100个、1000个和10000个脉冲，看看噪声幅值以及平均功率的变化。

仿真得到的结果如下：

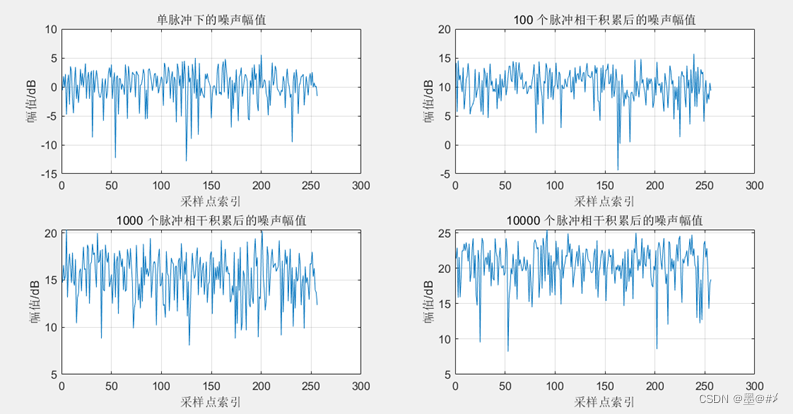
图2.1 不同数量脉冲相干积累下噪声幅值的变化

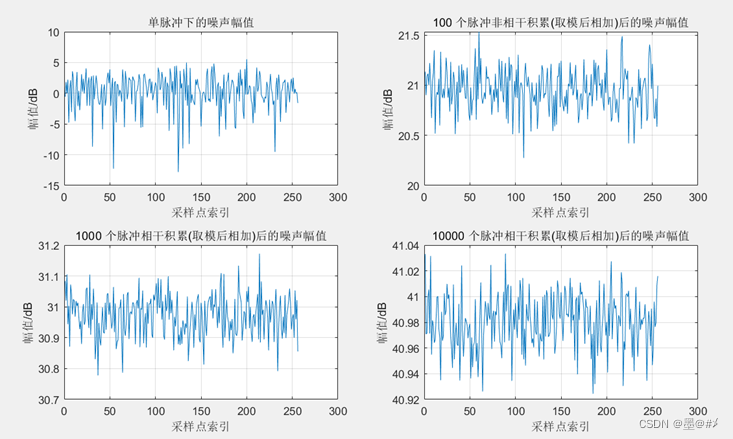
图2.2 不同数量脉冲非相干积累(取模后累加)下噪声幅值的变化

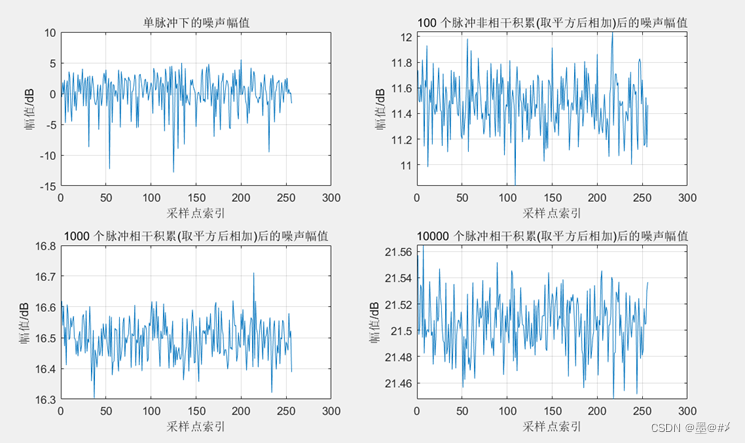
图2.3 不同数量脉冲非相干积累(求平方后累加)下噪声幅值的变化

并求得噪声的平均功率：

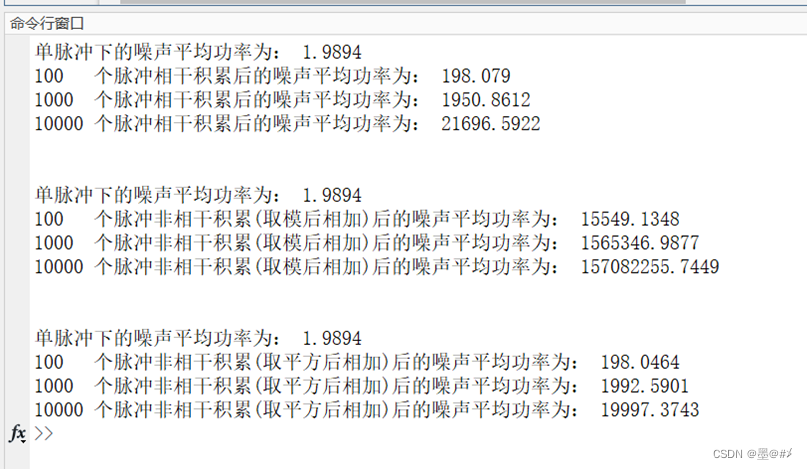
图2.4 不同数量脉冲相干&非相干积累下噪声功率的变化

从仿真的结果可知：

1. 相干(参)积累下，噪声的幅值有约sqrt(N)倍的提升(也即噪声的功率有N倍的提升，N为积累的脉冲数量)。

2. 以直接取模后相加的方式进行的非相干积累下，噪声的幅值有约N倍的提升(也即噪声的功率有N^2倍的提升，N为积累的脉冲数量)。

3. 以求平方后相加的方式进行的非相干积累下，噪声的幅值有约sqrt(N)倍的提升(也即噪声的功率有N倍的提升，N为积累的脉冲数量)。

后两种非相干积累下噪声的提升关系是符合预期的：因为各脉冲下都为白噪声，且相对独立，假设单脉冲下的幅值为a，功率为a^2，则N次累加下：

取模后相加时，其幅值变成：N*a，功率变成：N^2*a^2;

求平方后相加时，其功率变成：N*a^2，幅值变成：sqrt(N*a^2) = sqrt(N)*a。

2.2 相干&非相干积累下SNR的变化

在2.1的基础上，本节在原有噪声的基础上，在索引值为100处增加一个幅值为5的信号点(可以理解成该信号骑在噪底上)。同样地，分别通过：直接相加、取模后相加、取平方后相加的方式，分别累加100个、1000个和10000个脉冲，看看信号功率、以及SNR的变化。

仿真的结果如下：

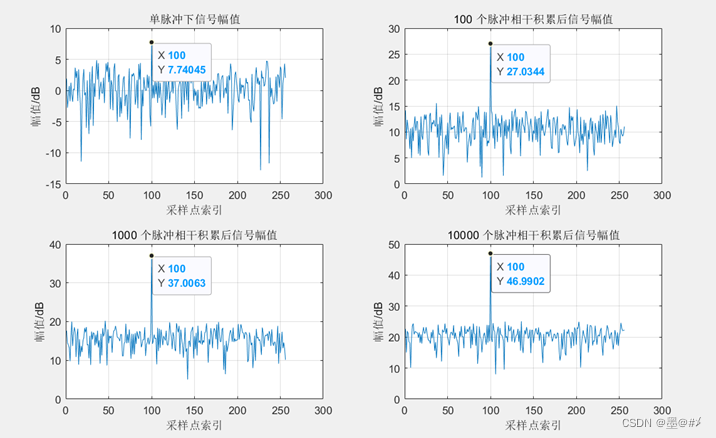
图2.5 不同数量脉冲相干积累下信后幅值的变化

图2.6 不同数量脉冲非相干积累(取模后累加)下信号幅值的变化

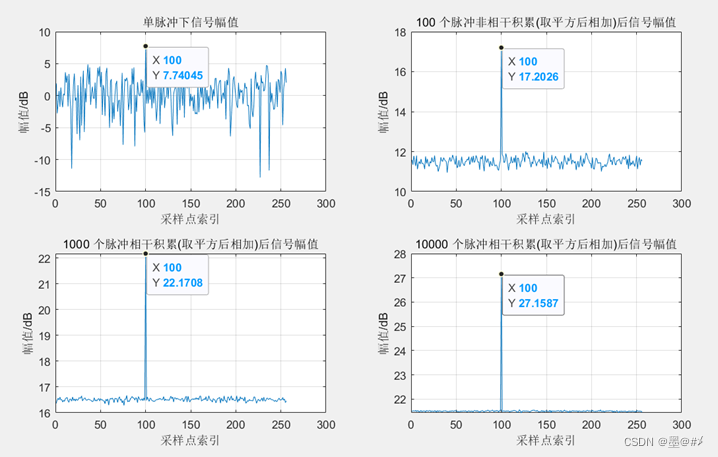
图2.7 不同数量脉冲非相干积累(求平方后累加)下噪声幅值的变化

在得到的信号功率和噪声均值功率（这里的噪声功率我用的2.1节中得到的噪声功率，虽然本节的噪声信号我是重新随机生成的，但都是白噪声，所以区别不是很大）的基础上，基于公式(1-1)求得SNR:

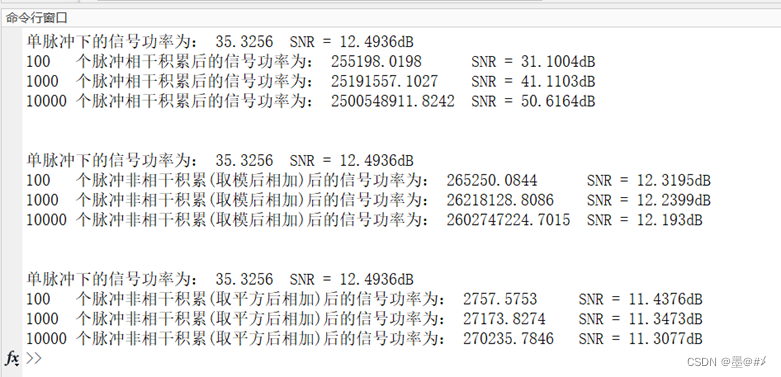
图2.8 不同数量脉冲相干&非相干积累下信号功率&SNR的变化

从仿真的结果来看：

1. 相干(参)积累下，信号的幅值有约N倍的提升(也即功率有约N^2倍的提升，N为脉冲积累的个数)，结合2.1节的噪声提升幅度，可知SNR有约N倍的提升，仿真结果显示，单脉冲下的SNR为12.4936dB,100个脉冲相干积累后，SNR提升了约20dB到31.1004dB，也即提高了约100倍，1000个和10000个脉冲相干积累后结论类似。

2. 以直接取模后相加的方式进行的非相干积累下，信号的幅值有约N倍的提升(也即功率有约N^2倍的提升，N为脉冲积累的个数)，但同时2.1节的仿真结果告诉我们噪声的提升幅度和信号的提升幅度一样，所以可以看到SNR并没有随积累数量的增加而增加。

3. 以求平方后相加的方式进行的非相干积累下，信号的幅值有约sqrt(N)倍的提升(也即信号的功率有N倍的提升，N为积累的脉冲数量)，同样地，2.1节的仿真结果告诉我们噪声的提升幅度和信号的提升幅度一样，所以SNR并不会随着脉冲积累而增加。

4. 一个有意思的现象是：随着积累数量的增加，噪声会变得更平坦，而且非相干积累时的趋势更显著，这是可以被解释的：经过一定数量的累加后(特别是取模或者取平方后累加)，会抹平各脉冲之间噪声幅值的随机性，从而使得各个采样点(或距离门)下的幅值趋于一致。

5. 因为图中纵坐标是取10*lg后的结果，还有一点可能无法在图中直观表示出来：在非相干积累中，虽然SNR没有随脉冲数的增加而改善，但是信号和噪声之间的幅值差值是在增加的！

5. 4和5，似乎对CFAR检测有一些帮助。

7. 仿真2.1和2.2的仿真结果验证了第一章中结论的正确性：N个脉冲下相干(参)积累下的SNR可以提升N倍，而非相干积累对SNR没有提高！

2.3 单脉冲下信号幅值低于噪底的信号在相干&非相干积累后的表现

在前面两节的基础上，本节仿真：单脉冲时信号低于噪底的情况下，随着脉冲积累数量的增加，我们是否可以基于相干积累把信号找出来，并与前两节得到的结论做相互验证。

因为随着脉冲数量的增加，数据量会急剧增加，本节的仿真中，我们设置单脉冲的点数为64个点，生成1e6个脉冲，设置两个信号：信号1的索引值为20，该信号在单脉冲下的幅值大于噪底，信号2的索引值为40，该信号在单脉冲下的幅值约为噪底的1/100(也即SNR约为 -40dB)。分别积累100次、10000次和1e6次。

首先基于2.1的结论分析理论结果：我们至少需要10000个脉冲的相干积累才能使得SNR回到0(此时信号幅值和噪声幅值一样，不过考虑到噪底的随机性，此时信号还是可能会淹没在噪声中)，而经过1e6次积累后，SNR变成20dB，此时我们应该可以看到一个比较明显的信号波峰。

仿真的结果如下：

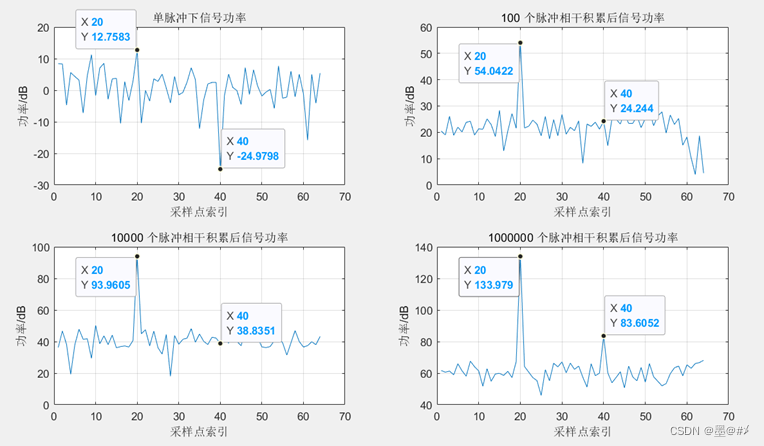
图2.9 不同脉冲数相干积累下信号功率变化

图2.10 不同脉冲数非相干积累下信号功率变化

由仿真的结果可知：

1. 相干积累下，信号2在单脉冲、积累100个、积累10000个脉冲下都会被淹没在噪声中，而积累1e6个脉冲后，该信号出现了！且从10000个到1e6个，脉冲数量增加了100倍，可以看到其功率增加了约40dB，SNR约有20dB的提升，结果符合预期。

2. 非相干积累下，因为SNR没有提高，单脉冲下淹没在噪底的信号会一直淹没在噪底中，结果符合预期。

2.4 本章小结

本章对多脉冲下的积累问题进行了较为详尽的仿真，可以得到如下有益结论：

1.不同积累方式下的幅值、功率以及SNR变化的相对关系如下(积累N个脉冲)：

表2.1 不同积累方式下的幅值、功率以及SNR变化关系列表

积累方式	噪声幅值	噪声功率	信号幅值	信号功率	SNR
相干积累	sqrt(N)倍	N倍	N倍	N^2倍	N倍
非相干积累(取幅值后累加)	N倍	N^2倍	N倍	N^2倍	不变
非相干积累(取平方后累加)	sqrt(N)倍	N倍	sqrt(N)倍	N倍	不变

2.单脉冲下淹没在噪底的信号可以通过相干积累的方式重新检测出。

3. 随着积累数量的增加，噪声会变得更平坦，而且非相干积累时的趋势更显著,当信号幅值大于噪底时，随着脉冲积累数量的增加，信号与幅值之间的差值会显著扩大(虽然SNR没有提高)。这两点可能对于CFAR检测有所帮助。

三、实测方案以及实测数据结果

第二章的仿真都是在很理想的情况下进行的：单距离门下只有一个目标、噪底也只有理想的高斯白噪声、没有考虑杂波干扰等等。所以有必要使用实测数据做进一步的实测分析和验证。

3.1 实验方案说明

本章我们基于Ti的AWR2944开发板进行实测数据采集，并探讨实测数据下相干以及非相干积累的效果（本章中的非相干积累只采用了取平方后累加这一种方式）。关于AWR2944开发板的介绍和使用说明读者可以去Ti的官网查看相关资料，我在之前的诸多博文中也使用了Ti的各开发板做过很多次实验，读者也可以找相关的博文及其所附的数据和代码参考。

本节只给出本章试验所用参数和试验方案说明。我们设计了室内和室外两组实验，室内下，将角反位于雷达正前方约2.5m处，如下图所示：

图3.1 室内试验现场图

表3.1 室内实验雷达参数列表

参数	值
收发天线数量	1T4R
起始频点	76GHz
发射脉宽	42us
Chirp调频斜率（AWR2944最高可到250MHz/us）	100MHz/us
Idle time	6us（在一帧一个chirp下该值不重要）
Chirp周期(单帧下发射一个chirp时，chirp周期等于帧周期)	42+6 = 48us
AD采样率	15MHz (AWR2944为单路采样)
采样起始点（延时）	5us
采样点数	512
单帧chirp数	1
帧周期	10ms
采集帧数（AWR2944可以设置的最大采样帧数为：65535）	10000
采集时长	10ms*10000 = 100s
数据总量	512141000016/8/1024/1024 = 39.0625MB

总发射带宽（AWR2944最高支持4.5GHz的带宽）	42e-6*100e12 = 4.2GHz
采样时长	512/15e6 = 34.13us
采样带宽	34.13e-6*100e12 = 3.4133GHz
理论距离分辨率	3e8/2/3.4133e9 = 0.0439m
理论最大测量距离(数据处理的角度)，(AWR2944的中频带宽是15MHz)	15MHz对应的最大距离为：15e63e8/100e12/2 = 22.5m 所设计参数对应的最大距离为：4.39e-2（512/2） = 11.24m。理论最大测量距离取其较小者：11.24m
AWR2944射频板天线3dB波束宽度	约±30°@水平；约±5°@俯仰

室外试验为将雷达板放置在窗口，斜向天空照射，试验现场图如下：

图3.2 室外实验现场图

室外实验下雷达参数设计列表如下：

表3.2 室外实验所用雷达参数列表

参数	值
收发天线数量	1T4R
起始频点	76GHz
发射脉宽	33us
Chirp调频斜率（AWR2944最高可到250MHz/us）	5MHz/us
Idle time	6us
Chirp周期(单帧下发射一个chirp时，chirp周期等于帧周期)	33+6 = 39us
AD采样率	20MHz (AWR2944为单路采样)
采样起始点（延时）	6us
采样点数	512
单帧chirp数	1
帧周期	5ms
采集帧数	100000
采集时长	5ms*100000 = 500s
数据总量	5121410000016/8/1024/1024/1024 = 0.38GB

总发射带宽（AWR2944最高支持4.5GHz的带宽）	33e-6*5e12 = 165MHz
采样时长	512/20e6 = 25.6us
采样带宽	25.6e-6*5e12 = 128MHz
理论距离分辨率	3e8/2/128e6 = 1.17m
理论最大测量距离(数据处理的角度)，(AWR2944的中频带宽是15MHz)	15MHz对应的最大距离为：15e63e8/5e12/2 = 450m 所设计参数对应的最大距离为：1.17（512/2） = 300m。理论最大测量距离取其较小者：300m
AWR2944射频板天线3dB波束宽度	约±30°@水平；约±5°@俯仰

注：本章的实测数据、数据解析和处理的参考代码以及第二章中的仿真代码我都附在了第六章，读者可以自行下载参考。

3.2 实测数据结果与分析

3.2.1 室内试验结果

在表3.1的参数设计下，对采集的数据进行解析后，我们可以得到一个大小为：512*10000*4大小的ADC数据矩阵，4表示4个接收通道，我们取其中一个接收通道的数据(大小为512*10000)，进行距离压缩 --- 取前一半的数据(AWR2944为单路采样) --- 分别用相干和非相干积累方法累加100个、1000个、10000个脉冲下的数据，得到的处理结果如下(为方便直观地看到SNR的大小，这里给出功率值，幅值是在其基础上减半)：

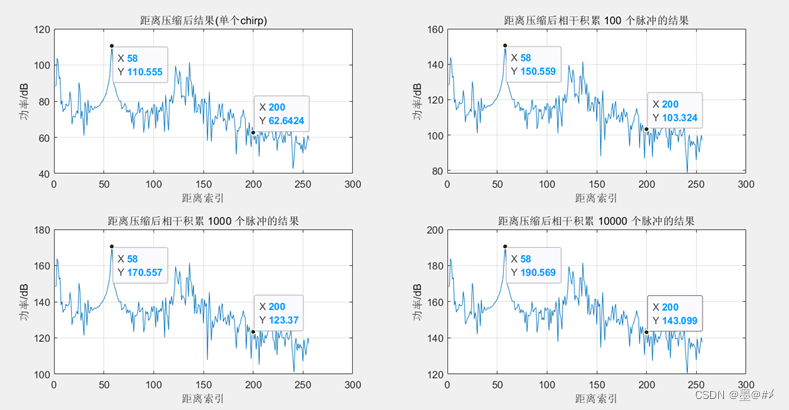
图3.3 不同脉冲数量相干积累后的结果

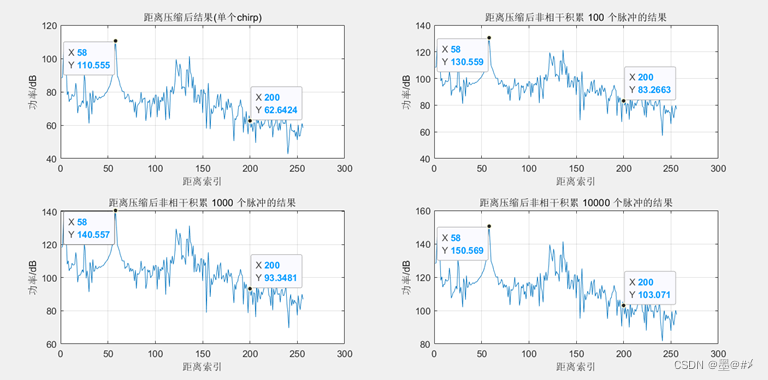
图3.4 不同脉冲数量非相干积累后的结果

从图示结果来看：

1. 在索引值58处有明显的波峰，该处即对应目标角反的位置，表3.1中给出了室内试验下的距离分辨率值为：0.0439m，58的索引值对应距离：2.5462m，与实验场景的设置吻合良好。

2. 如果我们以索引值为200处的点的幅值来估测噪底,以表2.1的结论来估测理论值，从图3.3以及图3.4中我们可以得到如下实测与理论值的对比 (表中的增加量都是针对单脉冲时的情况)：

表3.3 实测数据下不同脉冲积累数量相干积累下信号、噪声功率值变化列表

参数值	单脉冲	100个脉冲	1000个脉冲	10000个脉冲
信号功率值	110.555dB	150.559dB	170.557dB	190.569dB
理论信号功率值增加量(N^2倍)	-	40dB	60dB	80dB
实际信号功率值增加量	-	约40dB	约60dB	约80dB

噪底功率值	62.6424dB	103.324dB	123.37dB	143.099dB
理论噪底功率值增加量(N倍)	-	20dB	30dB	40dB
实际噪底功率值增加量	-	约40dB	约60dB	约80dB

SNR	47.9126dB	47.2350dB	47.1870dB	47.47dB
理论SNR增加量(N倍)	-	20dB	30dB	40dB
实际SNR增加量	-	0	0	0

表3.4 实测数据下不同脉冲积累数量非相干积累下信号、噪声功率变化列表

参数值	单脉冲	100个脉冲	1000个脉冲	10000个脉冲
信号功率值	110.555dB	130.559dB	140.557dB	150.569dB
理论信号功率值增加量(N倍)	-	20dB	30dB	40dB
实际信号功率值增加量	-	约20dB	约30dB	约40dB

噪底功率值	62.6424dB	83.2663dB	93.3481dB	103.071dB
理论噪底功率值增加量(N倍)	-	20dB	30dB	40dB
实际噪底功率值增加量	-	约20dB	约30dB	约40dB

SNR	47.9126dB	47.2927dB	47.2089dB	47.47dB
理论SNR增加量（0）	-	0dB	0dB	0dB
实际SNR增加量	-	0	0	0

室内试验结果分析

1. 信号在相干以及非相干积累下的功率增加都与理论值吻合良好。

2. 噪底在相干积累中的增加与信号的增加幅度一样！而导致SNR没有提高！这与理论是不符合的！当然，这不是说我们的理论是错误的，而是因为我们对噪底的估计是有误的,解释如下：

室内环境下有很多干扰(杂波)！可以说每个距离门里面都有干扰信号，（杂波是一个很有意思的概念，我在博文[4]中对这个概念有过一些探讨），所谓的杂波，其实本质上都是信号！(和距离2.5m处的角反本质上没有区别，只不过它们是我们不感兴趣的信号，所以我们将之归于所谓的杂波)。而这些杂波在多脉冲之间和目标信号一样是相干的！所以在做相干积累时，其功率增加的幅度与目标信号一样，所以如果我们以索引值为200处点的幅值做噪底估计时，SNR并没有提高(更准确地说，应该是信杂比没有提高)。

3. 第2点的结论不是说相干积累在实际的工程应用中没有用：比如我们可以通过通道之间的相干积累将波束指向特定的角度，可以增加该特定角度下目标的SNR，这也是我在之前的博文[1]中论述的内容之一； 此外在某些场景下可以规避干扰:比如探空，这也是我们要做室外实验进行进一步验证的原因和理论依据(规避干扰)。

3.2.2 室外试验结果

在表3.2的参数设计下，对采集的数据进行解析后，我们可以得到一个大小为：512*60000*4大小的ADC数据矩阵，4表示4个接收通道，我们取其中一个接收通道的数据(大小为512*60000)，进行距离压缩 --- 取前一半的数据(AWR2944为单路采样) --- 分别用相干和非相干积累方法累加600个、6000个、60000个脉冲下的数据，得到的处理结果如下。

注: 本实验下没有预设特定的目标物，场景限制，也没法完全规避杂波，本实验下我们主要关注相干积累下噪底的变化，以与3.2.1的实验结果相互验证。

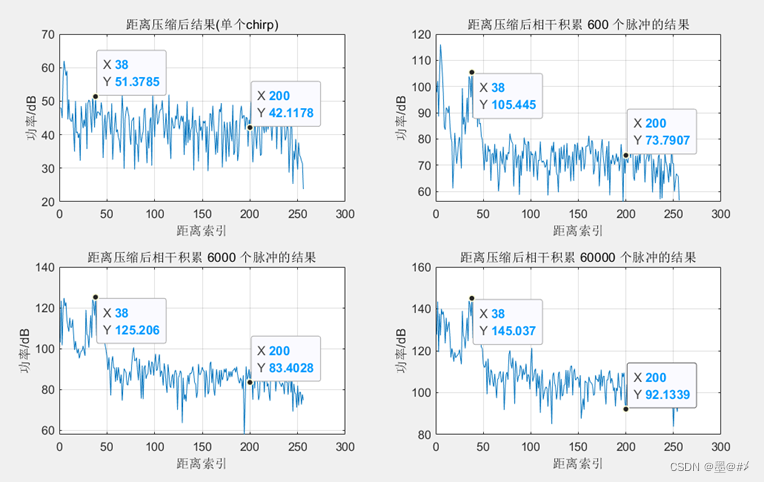
图3.5 不同脉冲数量相干积累后的结果

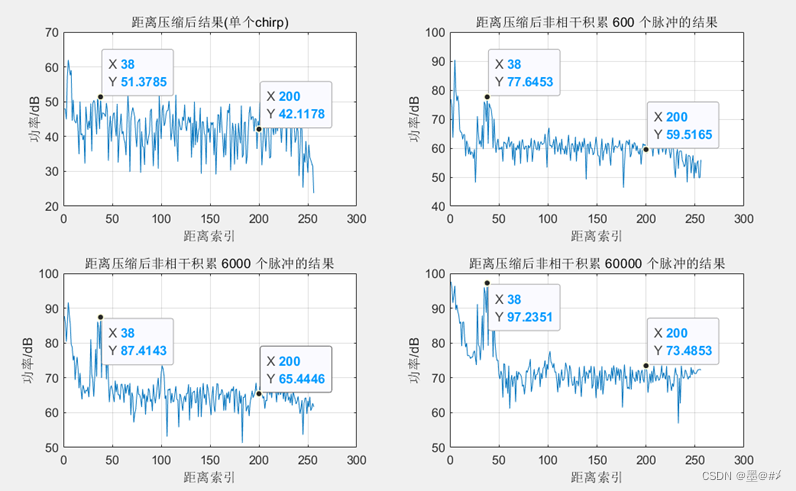
图3.6 不同脉冲数量非相干积累后的结果

可以看到在索引38处有凸起，我们以它为目标(也可以是杂波干扰)，以索引值为200处的点的幅值来估测噪底，将实测与理论列表如下：

表3.5 实测数据下不同脉冲积累数量相干积累下信号、噪声功率值变化列表

参数值	单脉冲	600个脉冲	6000个脉冲	60000个脉冲
信号功率值	51.3785dB	105.445dB	125.206 dB	145.037dB
理论信号功率值增加量(N^2倍)	-	55.563dB	75.563dB	95.563dB
实际信号功率值增加量	-	约54dB	约74dB	约94dB

噪底功率值	42.1178dB	73.7907dB	83.4028dB	92.1339dB
理论噪底功率值增加量(N倍)	-	27.7815dB	37.7815dB	47.7815dB
实际噪底功率值增加量	-	31.6729dB	41.285dB	50.016dB

SNR	9.2607dB	31.6543dB	41.8032dB	52.9031
理论SNR增加量（N倍）	-	27.7815dB	37.7815dB	47.7815dB
实际SNR增加量	-	22.3936dB	32.5425dB	43.6424dB

表3.6 实测数据下不同脉冲积累数量非相干积累下信号、噪声功率变化列表

参数值	单脉冲	100个脉冲	1000个脉冲	10000个脉冲
信号功率值	51.3785dB	77.6453dB	87.4143dB	97.2351dB
理论信号功率值增加量(N倍)	-	27.7815dB	37.7815dB	47.7815dB
实际信号功率值增加量	-	约26.27dB	约36.04dB	约45.86dB

噪底功率值	42.1178dB	59.5165dB	65.4446dB	73.4853dB
理论噪底功率值增加量(N倍)	-	27.7815dB	37.7815dB	47.7815dB
实际噪底功率值增加量	-	约17.40dB	约23.33dB	约31.37dB

SNR	9.2607dB	18.1288dB	21.9697dB	23.7498dB
理论SNR增加量(0)	-	0dB	0dB	0dB
实际SNR增加量	-	8.87dB	12.71dB	14.49dB

室外实验结果分析：

1. 从相干积累的结果来看，此次室外实验下信号与噪底功率随积累脉冲数的增加而增加的量都基本符合理论预期！SNR的增加也基本符合预期！说明我们此次选择的噪底估测位置下存在的杂波干扰很少(本次实验下，雷达的距离分辨率为1.17m，索引值200下对应的距离为234m，考虑到雷达对空，该距离门下只有较少的杂波是可以理解的)。 所以：本实验、室内试验以及仿真的结果都验证了表2.1结论的正确性！

2. 看到的一个比较有意思的现象是：在非相干积累下，SNR也有一定的提高！从表中来看，增加的SNR主要来源是噪声功率的增加幅度小于预期，但是可以看到不同积累脉冲数下的增加幅度没有太多相关性，结合室内试验时的结果，考虑原因是：在此室外实验下，距离索引200下的杂波幅值较小，其与噪声之间存在一定的概率相互抵消(导致某些脉冲下该处的幅值远低于平均水平)，从而使得在积累的过程中噪声幅值的增加小于预期。而在室内实验下，杂波的能量幅值远大于噪声，虽然也存在一定概率相互抵消，但是对幅值的影响很小。

3.2 本章小结

本章设计室内和室外两组实验，采集数据进行多脉冲下相干&非相干积累的实测数据分析。实测数据验证了表2.1结论的正确性，此外，更细节地：

1. 目标在相干以及非相干积累下的功率增加都与理论值吻合良好。

2. 实际应用中，如果有杂波存在于各距离门，且当杂波幅度远大于噪底时，由于杂波的存在，相干和非相干积累下SCR(信杂比)不会有变化。

3. 实际应用中，如果有杂波的存在，但杂波幅值较小，其与噪声之间存在一定的概率相互抵消(导致某些脉冲下该处的幅值远低于平均水平)，从而使得在积累的过程中噪声幅值的增加小于预期，这会使得即便在非相干积累下也可能会有SNR的提升。

四、总结

本文围绕多脉冲积累下对SNR的影响这一问题展开，对多脉冲积累问题进行了系统介绍、详尽的仿真以及基于实测数据的分析讨论。在定性的理论分析、定量的仿真和实测数据结果支撑下，形成了以及验证了一些有益的定理和结论(见2.4以及3.2节)。本文的工作对多脉冲积累的应用(或各类相干/非相干积累应用)打下了基础。